Skip to main content

Advertisement

Springer Nature Link
Log in

Quantum correlations generation and distribution in a universal covariant quantum cloning circuit

  • Research Paper
  • Published:
Science China Information Sciences Aims and scope Submit manuscript

    We’re sorry, something doesn't seem to be working properly.

    Please try refreshing the page. If that doesn't work, please contact support so we can address the problem.

Abstract

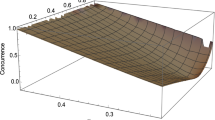
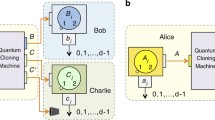
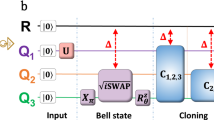
We discussed the distribution and generation of quantum correlations in a universal covariant quantum cloning circuit. Specifically, we first considered the distribution of quantum correlation, i.e., quantum discord, among the four qubits of the circuit. Then, we analyzed the generation of genuine 3- or 4-qubit entanglement in the cloning process. It is found that the circuit generates genuine 4-qubit GHZ (Greenberger-Horne-Zeilinger)-type state while only W-type 3-qubit state could be generated. These results illustrate the special quantum correlation manipulation capabilities of the cloning circuit.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

References

  1. Wootters W K, Zurek W H. A single quantum cannot be cloned. Nature (London), 1982, 299: 802–803

    Article  Google Scholar 

  2. Scarani V, Iblisdir S, Gisin N, et al. Quantum cloning. Rev Mod Phys, 2005, 77: 1225–1256

    Article  MathSciNet  MATH  Google Scholar 

  3. Fan H, Wang Y N, Jing L, et al. Quantum cloning machines and the applications. Phys Rep, 2014, 544: 241–322

    Article  MathSciNet  Google Scholar 

  4. Horodecki R, Horodecki P, Horodecki M, et al. Quantum entanglement. Rev Mod Phys, 2009, 81: 865–942

    Article  MathSciNet  MATH  Google Scholar 

  5. Bužek V, Hillery M, Ziman M, et al. Programmable quantum processors. Quantum Inf Process, 2006, 5: 313–420

    Article  MathSciNet  MATH  Google Scholar 

  6. Li J, Chen X B, Sun X M, et al. Quantum network coding for multi-unicast problem based on 2D and 3D cluster states. Sci China Inf Sci, 2016, 59: 042301

    Article  Google Scholar 

  7. Zhang Z, Li J X, Liu L. Distributed state estimation and data fusion in wireless sensor networks using multi-level quantized innovation. Sci China Inf Sci, 2016, 59: 022316

    Google Scholar 

  8. Wang F, Luo M X, Li H R, et al. Improved quantum ripple-carry addition circuit. Sci China Inf Sci, 2016, 59: 042406

    Article  Google Scholar 

  9. Bužek V, Hillery M. Quantum copying: beyond the no-cloning theorem. Phys Rev A, 1996, 54: 1844–1852

    Article  MathSciNet  Google Scholar 

  10. Bužek V, Braunstein S L, Hillery M, et al. Quantum copying: a network. Phys Rev A, 1997, 56: 3446–3452

    Article  Google Scholar 

  11. Szabó L, Koniorczyk M, Adam P, et al. Optimal universal asymmetric covariant quantum cloning circuits for qubit entanglement manipulation. Phys Rev A, 2010, 81: 032323

    Article  Google Scholar 

  12. Wootters W K. Entanglement of formation of an arbitrary state of two qubits. Phys Rev Lett, 1998, 80: 2245–2248

    Article  Google Scholar 

  13. Ollivier H, Zurek W H. Quantum discord: a measure of the quantumness of correlations. Phys Rev Lett, 2002, 88: 017901

    Article  MATH  Google Scholar 

  14. Knill E, Laflamme R. Power of one bit of quantum information. Phys Rev Lett, 1998, 81: 5672–5675

    Article  Google Scholar 

  15. Datta A, Shaji A, Caves C M. Quantum discord and the power of one qubit. Phys Rev Lett, 2008, 100: 050502

    Article  Google Scholar 

  16. Coffman V, Kundu J, Wootters W K. Distributed entanglement. Phys Rev A, 2000, 61: 052306

    Article  Google Scholar 

  17. Verstraete F, Dehaene J, De Moor B, et al. Four qubits can be entangled in nine different ways. Phys Rev A, 2002, 65: 052112

    Article  MathSciNet  Google Scholar 

  18. Osterloh A, Siewert J. Constructing N-qubit entanglement monotones from antilinear operators. Phys Rev A, 2005, 72: 012337

    Article  Google Scholar 

  19. Ren X J, Jiang W, Zhou X, et al. Permutation-invariant monotones for multipartite entanglement characterization. Phys Rev A, 2008, 78: 012343

    Article  Google Scholar 

  20. Ren X J, Fan H. Quantum circuits for asymmetric 1 → n quantum cloning. Quantum Inf Comput, 2015, 15: 914–922

    MathSciNet  Google Scholar 

  21. Ali M, Rau A R P, Alber G. Quantum discord for two-qubit X states. Phys Rev A, 2010, 81: 042105

    Article  Google Scholar 

  22. Chen Q, Zhang C, Yu S, et al. Quantum discord of two-qubit X states. Phys Rev A, 2011, 84: 042313

    Article  Google Scholar 

  23. Ou Y C, Fan H. Bounds on negativity of superpositions. Phys Rev A, 2007, 76: 022320

    Article  Google Scholar 

  24. Yu C S, Yi X X, Song H S. Concurrence of superpositions. Phys Rev A, 2007, 75: 022332

    Article  Google Scholar 

  25. Song W, Liu N L, Chen Z B. Bounds on the multipartite entanglement of superpositions. Phys Rev A, 2007, 76: 054303

    Article  Google Scholar 

  26. Parashar P, Rana S. Entanglement and discord of the superposition of Greenberger-Horne-Zeilinger states. Phys Rev A, 2011, 83: 032301

    Article  Google Scholar 

Download references

Acknowledgements

This work was supported by National Natural Science Foundation of China (Grant No. U1204114).

Author information

Authors and Affiliations

  1. School of Physics and Electronics, Henan University, Kaifeng, 475000, China

    Xijun Ren

Authors
  1. Xijun Ren
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Xijun Ren.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Ren, X. Quantum correlations generation and distribution in a universal covariant quantum cloning circuit. Sci. China Inf. Sci. 60, 122501 (2017). https://doi.org/10.1007/s11432-016-0569-2

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s11432-016-0569-2

Keywords