Abstract
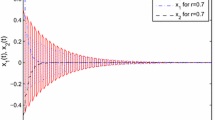
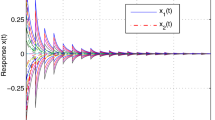
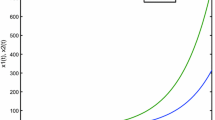
This paper considers the impulsive control of unstable neural networks with unbounded time-varying delays, where the time delays to be addressed include the unbounded discrete time-varying delay and unbounded distributed time-varying delay. By employing impulsive control theory and some analysis techniques, several sufficient conditions ensuring μ-stability, including uniform stability, (global) asymptotical stability, and (global) exponential stability, are derived. It is shown that an unstable delay neural network, especially for the case of unbounded time-varying delays, can be stabilized and has μ-stability via proper impulsive control strategies. Three numerical examples and their simulations are presented to demonstrate the effectiveness of the control strategy.
Similar content being viewed by others
References
Chua L, Yang L. Cellular neural networks: theory. IEEE Trans Circ Syst, 1988, 35: 1257–1272
Cohen M, Grossberg S. Absolute stability of global pattern formation and parallel memory storage by competitive neural networks. IEEE Trans Syst Man Cybern, 1983, 13: 815–826
Gao W, Zhou Z-H. Dropout rademacher complexity of deep neural networks. Sci China Inf Sci, 2016, 59: 072104
Li X, Song S. Impulsive control for existence, uniqueness and global stability of periodic solutions of recurrent neural networks with discrete and continuously distributed delays. IEEE Trans Neural Netw, 2013, 24: 868–877
Shen J C, Ma D, Gu Z H, et al. Darwin: a neuromorphic hardware co-processor based on spiking neural networks. Sci China Inf Sci, 2016, 59: 023401
Wu J. Introduction to Neural Dynamics and Signal Transmission Delay. New York: De Gruyter, 2001
Zeng Z, Wang J. Associative memories based on continuous-time cellular neural networks designed using space-invariant cloning templates. Neural Netw, 2009, 22: 651–657
Roska T, Chua L. Cellular neural networks with delay type template elements and nonuniform grids. Int J Circ Theory Appl, 1992, 20: 469–481
Roska T, Wu C, Balsi M, et al. Stability and dynamics of delay-type general and cellular neural networks. IEEE Trans Circ Syst I, 1992, 39: 487–490
Gilli M. Strange attractors in delayed cellular neural networks. IEEE Trans Circ Syst I, 1993, 40: 849–853
Zhang H G, Wang Z S. New delay-dependent criterion for the stability of recurrent neural networks with time-varying delay. Sci China Ser F-Inf Sci, 2009, 52: 942–948
Yang X, Cao J, Lu J. Synchronization of randomly coupled neural networks with Markovian jumping and time-delay. IEEE Trans Circ Syst I, 2013, 60: 363–376
Huang T, Li C, Duan S, et al. Robust exponential stability of uncertain delayed neural networks with stochastic perturbation and impulse effects. IEEE Trans Neural Netw, 2012, 23: 866–875
Huang Z K, Wang X H, Sannay M. Self-excitation of neurons leads to multiperiodicity of discrete-time neural networks with distributed delays. Sci China Inf Sci, 2011, 54: 305–317
Haykin S. Neural Networks. New Jersey: Prentice Hall, 1999
Niculescu S. Delay Effects on Stability: A Robust Control Approach. New York: Springer-Verlag, 2001
Gu K, Kharitonov V, Chen J. Stability of Time-Delay Systems. Boston: Birkhauser, 2003
Li X, Cao J. An impulsive delay inequality involving unbounded time-varying delay and applications. IEEE Trans Autom Control, 2017, 62: 3618–3625
Chen T, Wang L. Global μ-stability of delayed neural networks with unbounded time-varying delays. IEEE Trans Neural Netw, 2007, 18: 1836–1840
Chen T, Wang L. Global power-rate stability of dynamical systems with unbounded time-varying delays. IEEE Trans Circ Syst II, 2007, 54: 705–709
Zeng Z, Wang J, Liao X. Global asymptotic stability and the global exponential stability of neural networks with unbounded time-varying delays. IEEE Trans Circ Syst II, 2005, 52: 168–173
Velmurugan G, Rakkiyappan R, Cao J. Further analysis of global image-stability of complex-valued neural networks with unbounded time-varying delays. Neural Netw, 2015, 67: 14–27
Koo M, Choi H, Lim J. Output feedback regulation of a chain of integrators with an unbounded time-varying delay in the input. IEEE Trans Autom Control, 2012, 57: 2662–2667
Wang L, Chen T. Multiple μ-stability of neural networks with unbounded time-varying delays. Neural Netw, 2014, 53: 109–118
Yang T. Impulsive Systems and Control: Theory and Application. New York: Nova Science, 2001
Lakshmikantham V, Bainov D D, Simeonov P S. Theory of Impulsive Differential Equations. Singapore: World Scientific, 1989
Haddad W, Chellaboina V, Nersesov S. Impulsive and Hybrid Dynamcial Systems: Stability, Dissipativity and Control. New Jersey: Princeton University Press, 2006
Dashkovskiy S, Mironchenko A. Input-to-state stability of nonlinear impulsive systems. SIAM J Control Optim, 2012, 51: 1962–1987
Li X, Song S. Stabilization of delay systems: delay-dependent impulsive control. IEEE Trans Autom Control, 2017, 62: 406–411
Agranovich G, Litsyn E, Slavova A. Impulsive control of a hysteresis cellular neural network model. Nonlinear Anal Hybrid Syst, 2009, 3: 65–73
Lu J, Kurths J, Cao J, et al. Synchronization control for nonlinear stochastic dynamical networks: pinning impulsive strategy. IEEE Trans Neural Netw, 2012, 23: 285–292
Yang X, Cao J, Qiu J. p-moment exponential stochastic synchronization of coupled memristor-based neural networks with mixed delays via delayed impulsive control. Neural Netw, 2015, 65: 80–91
Liu X, Wang Q. Impulsive stabilization of high-order hopfield-type neural networks with time-varying delays. IEEE Trans Neural Netw, 2008, 19: 71–79
Li X, Regan D, Akca H. Global exponential stabilization of impulsive neural networks with unbounded continuously distributed delays. IMA J Appl Math, 2015, 80: 85–99
Guan Z, Liu Z, Feng G, et al. Synchronization of complex dynamical networks with time-varying delays via impulsive distributed control. IEEE Trans Circ Syst I, 2010, 57: 2182–2195
Guan Z, Hill D, Shen X. Hybrid impulsive and switching systems and application to control and synchronization. IEEE Trans Autom Control, 2005, 50: 1058–1062
Chen W, Lu X, Zheng W. Impulsive stabilization and impulsive synchronization of discrete-time delayed neural networks. IEEE Trans Neural Netw, 2015, 26: 734–748
Li X, Zhang X, Song S. Effect of delayed impulses on input-to-state stability of nonlinear systems. Automatica, 2017, 76: 378–382
Stamova I, Stamov T, Li X. Global exponential stability of a class of impulsive cellular neural networks with supremums. Int Adapt Control Signal Proces, 2014, 28: 1227–1239
Yao F Q, Deng F Q. Stability of impulsive stochastic functional differential systems in terms of two measures via comparison approach. Sci China Inf Sci, 2012, 55: 1313–1322
Li C, Wu S, Feng G, et al. Stabilizing effects of impulses in discrete-time delayed neural networks. IEEE Trans Neural Netw, 2011, 22: 323–329
Li X, Rakkiyappan R, Sakthivel N. Non-fragile synchronization control for Markovian jumping complex dynamical networks with probabilistic time-varying coupling delay. Asian J Control, 2015, 17: 1678–1695
Li X, Fu X. Effect of leakage time-varying delay on stability of nonlinear differential systems. J Franklin Inst, 2013, 350: 1335–1344
Acknowledgements
This work was jointly supported by National Natural Science Foundation of China (Grant Nos. 11301308, 61673247, 61273233), Outstanding Youth Foundation of Shandong Province (Grant Nos. ZR20170-2100145, ZR2016J L024), and Natural Sciences and Engineering Research Council of Canada.
Author information
Authors and Affiliations
Corresponding author
Additional information
Conflict of interest The authors declare that they have no conflict of interest.
Rights and permissions
About this article
Cite this article
Li, X., Song, S. & Wu, J. Impulsive control of unstable neural networks with unbounded time-varying delays. Sci. China Inf. Sci. 61, 012203 (2018). https://doi.org/10.1007/s11432-017-9097-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s11432-017-9097-1