Abstract
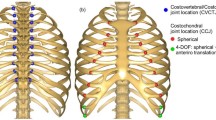
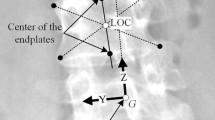
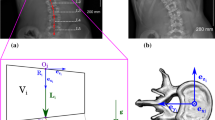
The distribution of stresses in the scoliotic spine is still not well known despite its biomechanical importance in the pathomechanisms and treatment of scoliosis. Gravitational forces are one of the sources of these stresses. Existing finite element models (FEMs), when considering gravity, applied these forces on a geometry acquired from radiographs while the patient was already subjected to gravity, which resulted in a deformed spine different from the actual one. A new method to include gravitational forces on a scoliotic trunk FEM and compute the stresses in the spine was consequently developed. The 3D geometry of three scoliotic patients was acquired using a multi-view X-ray 3D reconstruction technique and surface topography. The FEM of the patients’ trunk was created using this geometry. A simulation process was developed to apply the gravitational forces at the centers of gravity of each vertebra level. First the “zero-gravity” geometry was determined by applying adequate upwards forces on the initial geometry. The stresses were reset to zero and then the gravity forces were applied to compute the geometry of the spine subjected to gravity. An optimization process was necessary to find the appropriate zero-gravity and gravity geometries. The design variables were the forces applied on the model to find the zero-gravity geometry. After optimization the difference between the vertebral positions acquired from radiographs and the vertebral positions simulated with the model was inferior to 3 mm. The forces and compressive stresses in the scoliotic spine were then computed. There was an asymmetrical load in the coronal plane, particularly, at the apices of the scoliotic curves. Difference of mean compressive stresses between concavity and convexity of the scoliotic curves ranged between 0.1 and 0.2 MPa. In conclusion, a realistic way of integrating gravity in a scoliotic trunk FEM was developed and stresses due to gravity were explicitly computed. This is a valuable improvement for further biomechanical modeling studies of scoliosis.








Similar content being viewed by others
References
Arjmand N, Gagnon D, Plamondon A, Shirazi-Adl A, Lariviere C (2009) Comparison of trunk muscle forces and spinal loads estimated by two biomechanical models. Clin Biomech (Bristol, Avon) 24:533–541
Carrier J, Aubin CE, Villemure I, Labelle H (2004) Biomechanical modeling of growth modulation following rib shortening or lengthening in adolescent idiopathic scoliosis. Med Biol Eng Comput 42:541–548
Clin J, Aubin CE, Labelle H (2007) Virtual prototyping of a brace design for the correction of scoliotic deformities. Med Biol Eng Comput 45:467–473
Delorme S, Labelle H, Poitras B, Rivard CH, Coillard C, Dansereau J (2000) Pre-, intra-, and postoperative three-dimensional evaluation of adolescent idiopathic scoliosis. J Spinal Disord 13:93–101
Delorme S, Petit Y, de Guise JA, Labelle H, Aubin CE, Dansereau J (2003) Assessment of the 3D reconstruction and high-resolution geometrical modeling of the human skeletal trunk from 2-D radiographic images. IEEE Trans Biomed Eng 50:989–998
Driscoll M, Aubin CE, Moreau A, Villemure I, Parent S (2009) The role of spinal concave-convex biases in the progression of idiopathic scoliosis. Eur Spine J 18:180–187
El-Rich M, Shirazi-Adl A (2005) Effect of load position on muscle forces, internal loads and stability of the human spine in upright postures. Comput Methods Biomech Biomed Eng 8:359–368
Fortin D, Cheriet F, Beausejour M, Debanne P, Joncas J, Labelle H (2007) A 3D visualization tool for the design and customization of spinal braces. Comput Med Imaging Graph 31:614–624
Gram MC, Hasan Z (1999) The spinal curve in standing and sitting postures in children with idiopathic scoliosis. Spine 24:169–177
Huynh AM, Aubin CE, Rajwani T, Bagnall KM, Villemure I (2007) Pedicle growth asymmetry as a cause of adolescent idiopathic scoliosis: a biomechanical study. Eur Spine J 16:523–529
Klepps SJ, Lenke LG, Bridwell KH, Bassett GS, Whorton J (2001) Prospective comparison of flexibility radiographs in adolescent idiopathic scoliosis. Spine 26:E74–E79
Krag MH, Cohen MC, Haugh LD, Pope MH (1990) Body height change during upright and recumbent posture. Spine 15:202–207
Liu YK, Laborde JM, Van Buskirk WC (1971) Inertial properties of a segmented cadaver trunk: their implications in acceleration injuries. Aerosp Med 42:650–657
Mannion AF, Meier M, Grob D, Muntener M (1998) Paraspinal muscle fibre type alterations associated with scoliosis: an old problem revisited with new evidence. Eur Spine J 7:289–293
Matsumoto T, Ohnishi I, Bessho M, Imai K, Ohashi S, Nakamura K (2009) Prediction of vertebral strength under loading conditions occurring in activities of daily living using a computed tomography-based nonlinear finite element method. Spine (Phila Pa 1976) 34:1464–1469
Meir AR, Fairbank JC, Jones DA, McNally DS, Urban JP (2007) High pressures and asymmetrical stresses in the scoliotic disc in the absence of muscle loading. Scoliosis 2:4
Nachemson AL (1981) Disc pressure measurements. Spine 6:93–97
Patwardhan AG, Havey RM, Meade KP, Lee B, Dunlap B (1999) A follower load increases the load-carrying capacity of the lumbar spine in compression. Spine 24:1003–1009
Pazos V, Cheriet F, Danserau J, Ronsky J, Zernicke RF, Labelle H (2007) Reliability of trunk shape measurements based on 3-D surface reconstructions. Eur Spine J 16:1882–1891
Pearsall DJ, Reid JG, Ross R (1994) Inertial properties of the human trunk of males determined from magnetic resonance imaging. Ann Biomed Eng 22:692–706
Pearsall DJ, Reid JG, Livingston LA (1996) Segmental inertial parameters of the human trunk as determined from computed tomography. Ann Biomed Eng 24:198–210
Petit Y, Aubin CE, Labelle H (2004) Patient-specific mechanical properties of a flexible multi-body model of the scoliotic spine. Med Biol Eng Comput 42:55–60
Roaf R (1960) Vertebral growth and its mechanical control. J Bone Joint Surg (Br) 42-B:40–59
Rohlmann A, Zander T, Rao M, Bergmann G (2009) Applying a follower load delivers realistic results for simulating standing. J Biomech 42:1520–1526
Rohlmann A, Zander T, Rao M, Bergmann G (2009) Realistic loading conditions for upper body bending. J Biomech 42:884–890
Stokes IA (2007) Analysis and simulation of progressive adolescent scoliosis by biomechanical growth modulation. Eur Spine J 16:1621–1628
Stokes IA, Gardner-Morse M (2004) Muscle activation strategies and symmetry of spinal loading in the lumbar spine with scoliosis. Spine 29:2103–2107
Vedantam R, Lenke LG, Bridwell KH, Linville DL (2000) Comparison of push-prone and lateral-bending radiographs for predicting postoperative coronal alignment in thoracolumbar and lumbar scoliotic curves. Spine 25:76–81
Villemure I, Aubin CE, Dansereau J, Labelle H (2004) Biomechanical simulations of the spine deformation process in adolescent idiopathic scoliosis from different pathogenesis hypotheses. Eur Spine J 13:83–90
Wilke HJ, Neef P, Caimi M, Hoogland T, Claes LE (1999) New in vivo measurements of pressures in the intervertebral disc in daily life. Spine 24:755–762
Wong C, Gehrchen PM, Kiaer T (2008) Can experimental data in humans verify the finite element-based bone remodeling algorithm? Spine (Phila Pa 1976) 33:2875–2880
Acknowledgments
This study was funded by the Natural Sciences and Engineering Research Council of Canada.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Clin, J., Aubin, CÉ., Lalonde, N. et al. A new method to include the gravitational forces in a finite element model of the scoliotic spine. Med Biol Eng Comput 49, 967–977 (2011). https://doi.org/10.1007/s11517-011-0793-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11517-011-0793-4