Skip to main content
Springer Nature Link
Log in

Towards optimum chest compression performance during constant peak displacement cardiopulmonary resuscitation

  • Original Article
  • Published:
Medical & Biological Engineering & Computing Aims and scope Submit manuscript

Abstract

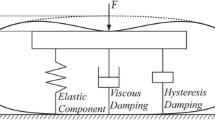
The aim of this study is to determine the conditions necessary to achieve optimum chest compression (CC) performance during constant peak displacement cardiopulmonary resuscitation (CPR). This was accomplished by first performing a sensitivity analysis on a theoretical constant peak displacement CPR CC model to identify the parameters with the highest sensitivity. Next, the most sensitive parameters were then optimized for net sternum-to-spine compression depth, using a two-variable non-linear least squares method. The theoretical CC model was found to be most sensitive to: thoracic stiffness, maximum sternal displacement, CC rate, and back support stiffness. Based on a two-variable, non-linear least squares analysis to optimize the model for the net sternum-to-spine compression depth during constant peak displacement CPR, it was found that the optimum ranges for the CC rate and back support stiffness are between 40–120 cpm and 241.0–1198.5 Ncm−1, respectively. Clinically, this suggests that current ERC guidelines for the CC rate during peak displacement CPR are appropriate; however, practitioners should be aware that the stiffness of the back support surfaces found in many hospitals may be sub-optimal and should consider using a backboard or a concrete floor to enhance CPR effectiveness.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5

Similar content being viewed by others

Abbreviations

m 1 :

Sternal mass (g)

m 2 :

Thoracic mass (g)

μ 1 :

Sternal damping coefficient (Ncm−1 s−1)

μ 2 :

Back support damping coefficient (Ncm−1 s−1)

k 1 :

Sternal spring constant (Ncm−1)

k 2 :

Back support spring constant (Ncm−1)

r :

Residual (cm)

t :

Time (s)

x :

Displacement (cm)

x 1 :

Absolute sternal displacement (cm)

x 1,max :

Maximum sternal displacement (cm)

x 2 :

Back support displacement (cm)

ω :

Angular frequency of compression (rads−1)

References

  1. Mathworks Inc. (2010) MATLAB Function Reference—lsqcurvefit. http://www.mathworks.com/support/tech-notes/1500/1508.html#section2. Accessed 30 Sept 2010

  2. Andersen LØ, Isbye DL, Rasmussen LS (2007) Increasing compression depth during manikin CPR using a simple backboard. Acta Anaesthesiologica Scand 51:747–750

    Article  CAS  Google Scholar 

  3. Aufderheide TP, Lurie KG (2004) Death by hyperventilation: a common and life-threatening problem during cardiopulmonary resuscitation. Crit Care Med 32(9):S345–S351

    Article  PubMed  Google Scholar 

  4. Babbs CF, Kern KB (2002) Optimum compression to ventilation ratios in CPR under realistic, practical conditions: a physiological and mathematical analysis. Resuscitation 54:147–157

    Article  PubMed  Google Scholar 

  5. Babbs CF, Nadkarni V (2004) Optimizing chest compression to rescue ventilation ratios during one-rescuer CPR by professionals and lay persons: children are not just little adults. Resuscitation 61:173–181

    Article  PubMed  Google Scholar 

  6. Bates DM, Watts DG (1988) Nonlinear regression analysis and its applications. Wiley, New York, pp 39–66

    Book  Google Scholar 

  7. Boe JM, Babbs CF (1999) Mechanics of cardiopulmonary resuscitation performed with the patient on a soft bed vs. a hard surface. Acad Emerg Med 6(7):754–757

    Article  PubMed  CAS  Google Scholar 

  8. Braga MS, Dominguez TE, Pollock AN, Niles D et al (2009) Estimation of optimal CPR chest compression depth in children by using computer tomography. Pediatrics 124:69–74

    Article  Google Scholar 

  9. Cloete G, Dellimore KHJ, Scheffer C (2011) Investigation of the impact of backboard orientation and size on chest compressions during cardiopulmonary resuscitation. Accepted by Acad Emerg Med, Manuscript ID 2011AEMJ-11-105

  10. European Resuscitation Council (2010) Guidelines for Resuscitation 2010 Section 1. Executive summary. Resuscitation 81:1219–1276

  11. Fenele MP, Maier GW, Kern KB et al (1988) Influence of compression rate on initial success of resuscitation and 24 hour survival after prolonged manual cardiopulmonary resuscitation in dogs. Circulation 77:240–250

    Article  Google Scholar 

  12. Fenici P, Idris AH, Lurie KG, Ursella S, Gabrielli A (2005) What is the optimal chest compression-ventilation ratio? Curr Opin Crit Care 11:204–211

    Article  PubMed  Google Scholar 

  13. Gruben KG, Guerci AD, Popel AS, Tsitlik JE (1993) Sternal force–displacement relationship during cardiopulmonary resuscitation. J Biomech Eng 115:195–201

    Article  PubMed  CAS  Google Scholar 

  14. Halperin HR, Tsitlik JE, Guerci AD et al (1986) Determinants of blood flow to vital organs during cardiopulmonary resuscitation in dogs. Circulation 73:539–550

    Article  PubMed  CAS  Google Scholar 

  15. Kern KB, Sanders AB, Raife J et al (1992) A study of chest compression rates during cardiopulmonary resuscitation in humans: the importance of rate-directed chest compressions. Arch Internal Med 152:145–149

    Article  CAS  Google Scholar 

  16. Kouwenhoven WB, Jude JR, Knickerbocker GG (1960) Closed-chest cardiac massage. J Amer Med Assoc 173:1064–1067

    CAS  Google Scholar 

  17. Nishisaki A, Nysaether J, Sutton R et al (2009) Effect of mattress deflection on CPR quality assessment for older children and adolescents. Resuscitation 80:540–545

    Article  PubMed  Google Scholar 

  18. Nolan JP, Deakin CD, Soar J et al (2005) European Resuscitation Council Guidelines for Resuscitation. Section 4. Adult advanced life support. Resuscitation 67S1:S39–86

  19. Noordergraaf GJ, Paulussen IWF, Venema A et al (2009) The impact of compliant surfaces on in-hospital chest compressions: effects of common mattresses and a backboard. Resuscitation 80:546–552

    Article  PubMed  Google Scholar 

  20. Perkins GD, Soar J (2005) In hospital cardiac arrest: missing links in the chain of survival. Resuscitation 66:253–255

    Article  PubMed  Google Scholar 

  21. Perkins GD, Benny R, Giles S et al (2003) Do different mattresses affect the quality of cardiopulmonary resuscitation? Intensive Care Med 29:2330–2335

    Article  PubMed  Google Scholar 

  22. Perkins GD, Smith CM, Augre C et al (2006) Effects of a backboard, bed height, and operator position on compression depth during simulated resuscitation. Intensive Care Med 32:1632–1635

    Article  PubMed  Google Scholar 

  23. Safar P, Escarraga LA, Elam JO (1958) A comparison of the mouth-to-mouth and mouth-to airway methods of artificial respiration with the chest-pressure arm-lift methods. N Eng J Med 258:671–677

    Article  CAS  Google Scholar 

  24. Turner I, Turner S (2004) Optimum cardiopulmonary resuscitation for basic and advanced life support: a simulation study. Resuscitation 62:209–217

    Article  PubMed  CAS  Google Scholar 

  25. Tweed M, Tweed C, Perkins GD (2001) The effect of differing support surfaces on the efficacy of chest compressions using a resuscitation manikin model. Resuscitation 51:179–183

    Article  PubMed  CAS  Google Scholar 

  26. Wyckoff MH, Berg RA (2008) Optimizing chest compressions during delivery-room resuscitation. Semin Fetal Neonatal Med 13:410–1415

    Article  PubMed  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mechanical and Mechatronic Engineering, University of Stellenbosch, Private Bag X1 Matieland, Stellenbosch, 7602, Western Cape, South Africa

    Kiran H. J. Dellimore, Garth Cloete & Cornie Scheffer

Authors
  1. Kiran H. J. Dellimore
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Garth Cloete
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Cornie Scheffer
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Cornie Scheffer.

Appendix

Appendix

The equations governing the chest compression (CC) depth can be expressed in terms of the two most sensitive variables, back support stiffness (k 2) and CC rate, as follows:

$$ x_{1} = \frac{{x_{1,\max } }}{2}\left[ {1 - \cos \left( {\frac{{2\pi \;{\text{CCrate}} \cdot t}}{60}} \right)} \right] $$
(10)
$$ x_{2} = a\left( {{\text{CCrate}},k_{2} } \right)\sin \left( {\frac{{2\pi {\text{CCrate}} \cdot t}}{60}} \right) + b\left( {{\text{CCrate}},k_{2} } \right)\cos \left( {\frac{{2\pi {\text{CCrate}} \cdot t}}{60}} \right) + {F \mathord{\left/ {\vphantom {F {\left( {k_{1} + k_{2} } \right)}}} \right. \kern-\nulldelimiterspace} {\left( {k_{1} + k_{2} } \right)}} $$
(11)

In Eqs. 10 and 11, a(CCrate, k 2) implies a = f(CCrate, k 2) and b(CCrate, k 2 ) implies b = f(CCrate, k 2) where f indicates ‘function of’, such that a(CCrate, k 2) and b(CCrate, k 2) are defined as follows:

$$ a\left( {{\text{CCrate}},k_{2} } \right) = \frac{{\left( {\frac{{\mu_{1} x_{1,\max } }}{2}} \right)\left( {\frac{{2\pi {\text{CCrate}}}}{60}} \right)\left[ {k_{1} + k_{2} - A\left( {\frac{{2\pi {\text{CCrate}}}}{60}} \right)^{2} } \right] + BE\left( {\frac{{2\pi {\text{CCrate}}}}{60}} \right)}}{{B^{2} \left( {\frac{{2\pi {\text{CCrate}}}}{60}} \right)^{2} + \left[ {k_{1} + k_{2} - A\left( {\frac{{2\pi {\text{CCrate}}}}{60}} \right)^{2} } \right]^{2} }} $$
(12)
$$ b\left( {{\text{CCrate}},k_{2} } \right) = \frac{{E\left[ {k_{1} + k_{2} - A\left( {\frac{{2\pi {\text{CCrate}}}}{60}} \right)^{2} } \right] - B\left( {\frac{{\mu_{1} x_{1,\max } }}{2}} \right)\left( {\frac{{2\pi {\text{CCrate}}}}{60}} \right)^{2} }}{{B^{2} \left( {\frac{{2\pi {\text{CCrate}}}}{60}} \right)^{2} + \left[ {k_{1} + k_{2} - A\left( {\frac{{2\pi {\text{CCrate}}}}{60}} \right)^{2} } \right]^{2} }} $$
(13)

Subtracting Eqs. 11 from 10 yields an expression for the net sternum-to-spine compression depth, g = x 1 − x 2:

$$ \begin{gathered} g = x_{1} - x_{2} = \frac{{x_{1,\max } }}{2}\left[ {1 - \cos \left( {\frac{{2\pi {\text{CCrate}} \cdot t}}{60}} \right)} \right] - a\left( {{\text{CCrate}},k_{2} } \right)\sin \left( {\frac{{2\pi {\text{CCrate}} \cdot t}}{60}} \right) \hfill \\ - b\left( {{\text{CCrate}},k_{2} } \right)\cos \left( {\frac{{2\pi {\text{CCrate}} \cdot t}}{60}} \right) - {F \mathord{\left/ {\vphantom {F {\left( {k_{1} + k_{2} } \right)}}} \right. \kern-\nulldelimiterspace} {\left( {k_{1} + k_{2} } \right)}} \hfill \\ \end{gathered} $$
(14)

Next, differentiating f in Eq. 14 with respect to each variable gives the Jacobian matrix:

$$ A = \left| {{{ \, \partial g\left( {{\text{CCrate}},k_{2} } \right)} \mathord{\left/ {\vphantom {{ \, \partial g\left( {{\text{CCrate}},k_{2} } \right)} {\partial {\text{CCrate}}}}} \right. \kern-\nulldelimiterspace} {\partial {\text{CCrate}}}}\,{{\partial g\left( {{\text{CCrate}},k_{2} } \right)} \mathord{\left/ {\vphantom {{\partial g\left( {{\text{CCrate}},k_{2} } \right)} {\partial k_{2} }}} \right. \kern-\nulldelimiterspace} {\partial k_{2} }}} \right| $$
(15)

where \(\partial g({\text{CCrate}},k_{2} )/\partial {\text{CCrate and}}\;\partial g({\text{CCrate}},k_{2} )/\partial k_{2}\) respectively, are given by:

$$ \begin{gathered} {{ \, \partial g\left( {{\text{CCrate}},k_{2} } \right)} \mathord{\left/ {\vphantom {{ \, \partial g\left( {{\text{CCrate}},k_{2} } \right)} {\partial {\text{CCrate}} = \frac{{x_{1,\max } }}{2} \cdot }}} \right. \kern-\nulldelimiterspace} {\partial {\text{CCrate}} = \frac{{x_{1,\max } }}{2} \cdot }}\sin \left( {\frac{{2\pi {\text{CCrate}} \cdot t}}{60}} \right)\left( {\frac{2\pi \cdot t}{60}} \right) \hfill \\ \quad - a\left( {{\text{CCrate}},k_{2} } \right)\cos \left( {\frac{{2\pi {\text{CCrate}} \cdot t}}{60}} \right)\left( {\frac{2\pi \cdot t}{60}} \right) -{{\partial a\left( {{\text{CCrate}},k_{2} } \right)} \mathord{\left/ {\vphantom {{\partial a\left( {{\text{CCrate}},k_{2} } \right)} \partial }} \right. \kern-\nulldelimiterspace} \partial }{\text{CCrate}} \cdot \sin \left( {\frac{{2\pi {\text{CCrate}} \cdot t}}{60}} \right) \hfill \\ \quad + b\left( {{\text{CCrate}},k_{2} } \right)\sin \left( {\frac{{2\pi {\text{CCrate}} \cdot t}}{60}} \right)\left( {\frac{2\pi \cdot t}{60}} \right) - {{\partial b\left( {{\text{CCrate}},k_{2} } \right)} \mathord{\left/ {\vphantom {{\partial b\left( {{\text{CCrate}},k_{2} } \right)} \partial }} \right. \kern-\nulldelimiterspace} \partial }{\text{CCrate}} \cdot \cos \left( {\frac{{2\pi {\text{CCrate}} \cdot t}}{60}} \right) \hfill \\ \end{gathered} $$
(16)
$$ \begin{gathered} {{ \, \partial g\left( {{\text{CCrate}},k_{2} } \right)} \mathord{\left/ {\vphantom {{ \, \partial g\left( {{\text{CCrate}},k_{2} } \right)} {\partial k_{2} = {F \mathord{\left/ {\vphantom {F {\left( {k_{1} + k_{2} } \right)^{2} }}} \right. \kern-\nulldelimiterspace} {\left( {k_{1} + k_{2} } \right)^{2} }} - \sin \left( {\frac{{2\pi {\text{CCrate}} \cdot t}}{60}} \right) \cdot }}} \right. \kern-\nulldelimiterspace} {\partial k_{2} = {F \mathord{\left/ {\vphantom {F {\left( {k_{1} + k_{2} } \right)^{2} }}} \right. \kern-\nulldelimiterspace} {\left( {k_{1} + k_{2} } \right)^{2} }} - \sin \left( {\frac{{2\pi {\text{CCrate}} \cdot t}}{60}} \right) \cdot }}{{\partial a} \mathord{\left/ {\vphantom {{\partial a} {\partial k_{2} }}} \right. \kern-\nulldelimiterspace} {\partial k_{2} }}\left( {{\text{CCrate}},k_{2} } \right) \hfill \\ \quad - \cos \left( {\frac{{2\pi {\text{CCrate}} \cdot t}}{60}} \right) \cdot {{\partial b} \mathord{\left/ {\vphantom {{\partial b} {\partial k_{2} }}} \right. \kern-\nulldelimiterspace} {\partial k_{2} }}\left( {{\text{CCrate}},k_{2} } \right) \hfill \\ \end{gathered} $$
(17)

In Eqs. 16 and 17 \( {{\partial a} \mathord{\left/ {\vphantom {{\partial a} {\partial k_{2} }}} \right. \kern-\nulldelimiterspace} {\partial k_{2} }},\,{{\partial b} \mathord{\left/ {\vphantom {{\partial b} {\partial k_{2} }}} \right. \kern-\nulldelimiterspace} {\partial k_{2} }},\,{{\partial a} \mathord{\left/ {\vphantom {{\partial a} {\partial {\text{CCrate}}}}} \right. \kern-\nulldelimiterspace} {\partial {\text{CCrate}}}}\,{\text{and}}\,{{\partial b} \mathord{\left/ {\vphantom {{\partial b} {\partial {\text{CCrate}}}}} \right. \kern-\nulldelimiterspace} {\partial {\text{CCrate}}}} \) are defined as:

$$ \begin{gathered} {{ \, \partial a({\text{CCrate}},k_{2} )} \mathord{\left/ {\vphantom {{ \, \partial a({\text{CCrate}},k_{2} )} {\partial k_{2} = }}} \right. \kern-\nulldelimiterspace} {\partial k_{2} = }}\frac{{\left( {\frac{{\mu_{1} x_{1,\max } }}{2}} \right)\left( {\frac{{2\pi {\text{CCrate}}}}{60}} \right)}}{{B^{2} \left( {\frac{{2\pi {\text{CCrate}}}}{60}} \right)^{2} + \left[ {k_{1} + k_{2} - A\left( {\frac{{2\pi {\text{CCrate}}}}{60}} \right)^{2} } \right]^{2} }} \hfill \\ \quad - \left[ {2k_{1} + 2k_{2} - 2A\left( {\frac{{2\pi {\text{CCrate}}}}{60}} \right)^{2} } \right] \hfill \\ \cdot \left[ {\frac{{\left( {\frac{{\mu_{1} x_{1,\max } }}{2}} \right)\left( {\frac{{2\pi {\text{CCrate}}}}{60}} \right)\left( {k_{1} + k_{2} - A\left( {\frac{{2\pi {\text{CCrate}}}}{60}} \right)^{2} } \right) + BE\left( {\frac{{2\pi {\text{CCrate}}}}{60}} \right)}}{{\left( {B^{2} \left( {\frac{{2\pi {\text{CCrate}}}}{60}} \right)^{2} + \left[ {k_{1} + k_{2} - A\left( {\frac{{2\pi {\text{CCrate}}}}{60}} \right)^{2} } \right]^{2} } \right)^{2} }}} \right] \hfill \\ \end{gathered} $$
(18)
$$ \begin{gathered} {{ \, \partial b\left( {{\text{CCrate}},k_{2} } \right)} \mathord{\left/ {\vphantom {{ \, \partial b\left( {{\text{CCrate}},k_{2} } \right)} {\partial k_{2} = }}} \right. \kern-\nulldelimiterspace} {\partial k_{2} = }}\frac{E}{{B^{2} \left( {\frac{{2\pi {\text{CCrate}}}}{60}} \right)^{2} + \left[ {k_{1} + k_{2} - A\left( {\frac{{2\pi {\text{CCrate}}}}{60}} \right)^{2} } \right]^{2} }} \hfill \\ \quad - \left[ {2k_{1} + 2k_{2} - 2A\left( {\frac{{2\pi {\text{CCrate}}}}{60}} \right)^{2} } \right] \hfill \\ \cdot \left[ {\frac{{\left( {E\left( {k_{1} + k_{2} } \right) - A\left( {\frac{{2\pi {\text{CCrate}}}}{60}} \right)^{2} } \right) - B\left( {\frac{{\mu_{1} x_{1,\max } }}{2}} \right)\left( {\frac{{2\pi {\text{CCrate}}}}{60}} \right)^{2} }}{{\left( {B^{2} \left( {\frac{{2\pi {\text{CCrate}}}}{60}} \right)^{2} + \left[ {k_{1} + k_{2} - A\left( {\frac{{2\pi {\text{CCrate}}}}{60}} \right)^{2} } \right]^{2} } \right)^{2} }}} \right] \hfill \\ \end{gathered} $$
(19)
$$ \begin{gathered} {{ \, \partial a\left( {{\text{CCrate}},k_{2} } \right)} \mathord{\left/ {\vphantom {{ \, \partial a\left( {{\text{CCrate}},k_{2} } \right)} {\partial {\text{CCrate}} = }}} \right. \kern-\nulldelimiterspace} {\partial {\text{CCrate}} = }}\frac{{\left( {\frac{{\mu_{1} x_{1,\max } }}{2}} \right)\left( {\frac{2\pi }{60}} \right)\left( {k_{1} + k_{2} } \right) - 3A\left( {\frac{{\mu_{1} x_{1,\max } }}{2}} \right)\left( {\frac{2\pi }{60}} \right)^{3} {\text{CCrate}}^{2} + BE\left( {\frac{2\pi }{60}} \right)}}{{B^{2} \left( {\frac{{2\pi {\text{CCrate}}}}{60}} \right)^{2} + \left[ {k_{1} + k_{2} - A\left( {\frac{{2\pi {\text{CCrate}}}}{60}} \right)^{2} } \right]^{2} }} \hfill \\ \quad - \left[ {2B^{2} \left( {\frac{2\pi }{60}} \right)^{2} {\text{CCrate}} + 2\left( {k_{1} + k_{2} - A\left( {\frac{{2\pi {\text{CCrate}}}}{60}} \right)^{2} } \right) \cdot \left( { - 2A} \right)\left( {\frac{2\pi }{60}} \right)^{2} {\text{CCrate}}} \right] \hfill \\ \cdot \left[ {\frac{{\left( {\frac{{\mu_{1} x_{1,\max } }}{2}} \right)\left( {\frac{{2\pi {\text{CCrate}}}}{60}} \right)\left[ {k_{1} + k_{2} - A\left( {\frac{{2\pi {\text{CCrate}}}}{60}} \right)^{2} } \right] + BE\left( {\frac{{2\pi {\text{CCrate}}}}{60}} \right)}}{{\left( {B^{2} \left( {\frac{{2\pi {\text{CCrate}}}}{60}} \right)^{2} + \left[ {k_{1} + k_{2} - A\left( {\frac{{2\pi {\text{CCrate}}}}{60}} \right)^{2} } \right]^{2} } \right)^{2} }}} \right] \hfill \\ \end{gathered} $$
(20)
$$ \begin{gathered} {{ \, \partial b\left( {{\text{CCrate}},k_{2} } \right)} \mathord{\left/ {\vphantom {{ \, \partial b\left( {{\text{CCrate}},k_{2} } \right)} {\partial {\text{CCrate}} = }}} \right. \kern-\nulldelimiterspace} {\partial {\text{CCrate}} = }}\frac{{ - EA \cdot 2 \cdot \left( {\frac{2\pi }{60}} \right)^{2} {\text{CCrate}} - 2 \cdot B\left( {\frac{{\mu_{1} x_{1,\max } }}{2}} \right)\left( {\frac{2\pi }{60}} \right)^{2} {\text{CCrate}}}}{{B^{2} \left( {\frac{{2\pi {\text{CCrate}}}}{60}} \right)^{2} + \left[ {k_{1} + k_{2} - A\left( {\frac{{2\pi {\text{CCrate}}}}{60}} \right)^{2} } \right]^{2} }} \hfill \\ - \left[ {2B^{2} \left( {\frac{2\pi }{60}} \right)^{2} {\text{CCrate}} + 2\left( {k_{1} + k_{2} - A\left( {\frac{{2\pi {\text{CCrate}}}}{60}} \right)^{2} } \right) \cdot \left( { - 2A} \right)\left( {\frac{2\pi }{60}} \right)^{2} {\text{CCrate}}} \right] \hfill \\ \cdot \frac{{E\left[ {k_{1} + k_{2} - A\left( {\frac{{2\pi {\text{CCrate}}}}{60}} \right)^{2} } \right] - B\left( {\frac{{\mu_{1} x_{1,\max } }}{2}} \right)\left( {\frac{{2\pi {\text{CCrate}}}}{60}} \right)^{2} }}{{\left( {B^{2} \left( {\frac{{2\pi {\text{CCrate}}}}{60}} \right)^{2} + \left[ {k_{1} + k_{2} - A\left( {\frac{{2\pi {\text{CCrate}}}}{60}} \right)^{2} } \right]^{2} } \right)^{2} }} \hfill \\ \end{gathered} $$
(21)

Rights and permissions

Reprints and permissions

About this article

Cite this article

Dellimore, K.H.J., Cloete, G. & Scheffer, C. Towards optimum chest compression performance during constant peak displacement cardiopulmonary resuscitation. Med Biol Eng Comput 49, 1057–1065 (2011). https://doi.org/10.1007/s11517-011-0812-5

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11517-011-0812-5

Keywords