Abstract
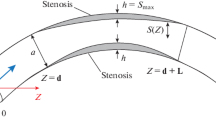
The unsteady flow characteristics of blood are analyzed through a catheterized stenotic artery with post-stenotic dilatation. A rigid tube with a pair of abnormal wall segments in close proximity to each other is employed to geometrically simulate the diseased artery. A micropolar fluid model is used to capture the rheological characteristics of the streaming blood in the annulus. The mild stenosis approximation is employed to derive the governing flow equation which is then solved using a robust finite difference method. Particular attention is paid to the effects of geometrical parameters of the arterial wall and rheological parameters of the blood on axial velocity, flow rate, resistance impedance and wall shear stress. The global behavior of blood is also analyzed through instantaneous pattern of streamlines.







Similar content being viewed by others
References
Abdullaha I, Amin N (2010) A micropolar fluid model of blood flow through a tapered artery with a stenosis. Math Methods Appl Sci 33:1910–1923
Anwar Bég O, Bhargava R, Rawat S, Takhar HS, Kalim Halim M (2008) Computational modeling of biomagnetic micropolar blood flow and heat transfer in a two-dimensional non-Darcian porous medium. Meccanica 43:391–410
Anwar Bég O, Bég TA, Bhargava R, Rawat S, Tripathi D (2012) Finite element study of pulsatile magneto-hemodynamic non-Newtonian flow and drug diffusion in a porous medium channel. J Mech Med Biol 12:1250081.1–1250081.26
Back LH (1994) Estimated mean flow resistance increase during coronary artery catheterization. J Biomech 27:169–175
Back LH, Denton TA (1992) Some arterial wall shear stress estimates in coronary angioplasty. Adv Biol Eng 22:337–340
Bathe KJ (1996) Finite element procedures. Addison Welsey, USA
Bathe M, Kamm RD (1999) A fluid–structure interaction finite element analysis of pulsatile blood flow through a compliant stenotic artery. ASME J Biomech Eng 121:361–369
Bhargava R, Sharma S, Anwar Bég O, Zueco J (2010) Finite element study of nonlinear two-dimensional deoxygenated biomagnetic micropolar flow. Commun Nonlinear Sci Numer Simul 15:1210–1233
Burton AC (1966) Physiology and biophysics of the circulation. Introductory text. Year Book Medical Publishers, Chicago
Caro CG, Fitzerald JM, Shroter RC (1971) Atheroma and arterial wall: shear observation, correlation and proposal of a shear dependent mass transfer mechanism for thermogenesis. Proc R Soc Lond Ser B 177:109–159
Chakravarty S, Mandal PK (1994) Mathematical modelling of blood flow through an overlapping arterial senosis. Math Comput Model 19:59–70
Chan WY, Ding Y, Tu JY (2007) Modeling of non-Newtonian blood flow through a stenosed artery incorporating fluid structure interaction. ANZIAM J 47:507–523
Chaturani P, Palanisamy V (1989) Micro-continuum model for pulsatile blood flow through a stenosed tube. Biorheology 26:835–846
Cokelet GR (1972) The rheology of human blood. In: Fung YC (ed) Biomechanics—its foundations and objectives. Prentice Hall, New York
Dabagh M, Vasava P, Jalah P (2015) Effects of severity and location of stenosis on the hemodynamics in human aorta and its branches. Med Biol Eng Comput 53:463–476
Dash RK, Jayaraman G, Metha KN (1996) Estimation of increased flow resistance in a narrow catheterized artery—a theoretical model. J Biomech 29:917–930
Dash RK, Jayaraman G, Mehta KN (1999) Flow in a catheterized curved artery with stenosis. J Biomech 32:49–61
Deplano V, Bertolotti C, Boiron O (2001) Numerical simulations of unsteady flows in a stenosed coronary bypass graft. Med Biol Eng Comput 39:488–499
Eringen AC (1966) Theory of micropolar fluids. J Math Mech 16:1–18
Eringen AC, Kang CK (1976) The effect of microstructure on the rheological properties of blood. Bull Math Biol 38:135–159
Feng R, Xenos M, Girdhar G, Kang W, Davenport JW, Deng Y, Bluestein D (2011) Viscous flow simulation in a stenosis model using discrete particle dynamics: a comparison between DPD and CFD. Mechanobiol, Biomech Model. doi:10.1007/s10237-011-0297
Fry DL (1973) Responses of the arterial wall to certain physical factors. In: Porter R, Knight J (eds) Atherogenesis: initiating factors. Association of Scientific Publishers, Amsterdam, pp 93–125
Hoffmann KA, Chiang ST (2000) Computational fluid dynamics. Engineering Edition System, Wichita
Jonasova A, Vimmr J (2011) Numerical simulation of non-Newtonian blood flow in bypass models. PAMM Proc Appl Math Mech 8:407–423
Kanai H, Iizuka M, Sakamoto K (1970) One of the problems in the measurement of blood pressure by catheter-insertion: wave reflection at the tip of the catheter. Med Biol Eng 8:483–496
Ling SC, Atabek HB (1972) A nonlinear analysis of pulsatile flow in arteries. J Fluid Mech 55:493–511
Mandal PK (2005) An unsteady analysis of non-Newtonian blood through tapered arteries with a stenosis. Int J Nonlinear Mech 40:151–164
Mekheimer KhS, El Kot MA (2008) The micropolar fluid model for blood flow through a tapered artery with a stenosis. Acta Mech Sin 24:637–644
Mekheimer KhS, Haroun MH, El Kot MA (2012) Influence of heat and chemical reactions on blood flow through an anisotropically tapered elastic arteries with overlapping stenosis. Appl Math Inf Sci 6:29–40
Moore KL (1990) Clinically oriented anatomy. Williams and Wilkins, Baltimore
Mustapha N, Amin N, Chakravarty S, Mandal PK (2009) Unsteady magnetohydrodynamic blood flow through irregular multi-stenosed arteries. Comput Biol Med 39:896–906
Muthu P, Kumar BVR, Chandra P (2008) A study of micropolar fluid in an annular tube with application to blood flow. J Mech Med Biol 4:561–576
Nazemi M, Kliestreuer C, Archie JP, Sorrell FY (1989) Fluid flow and plaque formation in an aortic formation. ASME J Biomech Eng 111:316–324
Pincombe B, Mazumdar JN (1997) The effects of post-stenotic dilatations on the flow of a blood analogue through stenosed coronary arteries. Math Comput Model 25:57–70
Pincombe B, Mazumdar J, Hamilton-Craig I (1999) Effects of multiple stenoses and post- stenotic dilatation on non-Newtonian blood flow in small arteries. Med Biol Eng Comput 37:595–599
Rana P, Anwar Bég O (2014) Mixed convection flow along an inclined permeable plate: effect of magnetic field, nanolayer conductivity and nanoparticle diameter. Appl Nanosci. doi:10.1007/s:13204-014-0352-z
Rana P, Bhargava R, Anwar Beg O (2013) Finite element simulation of unsteady MHD transport phenomena on a stretching sheet in a rotating nanofluid. Proc IMECHE Part N J Nanoeng Nanosyst 227:77–99
Reddy JVR, Srikanth D, Murthy K (2014) Mathematical modelling of pulsatile flow of blood through catheterized unsymmetric stenosed artery—effects of tapering angle and slip velocity. Eur J Mech B/Fluids 48:236–244
Rindfleish E (1972) Manual of pathological histology. New Syndemham Soc Lond 250:137–143
Sankar DS (2011) Two-phase non-linear model for blood flow in asymmetric and axi-symmetric stenosed arteries. Int J Non Linear Mech 46:296–305
Sankar DS, Hemalatha K (2007) Pulsatile flow of Herschel–Bulkley fluid through catheterized arteries—a mathematical model. Appl Math Model 31:1497–1517
Sankar DS, Hemalatha K (2007) A non-Newtonian fluid flow model for blood flow through a catheterized artery—steady flow. Appl Math Model 31:1847–1864
Sankar DS, Lee U (2008) Two-fluid non-linear model for flow in catheterized blood vessels. Int J Non Linear Mech 43:622–631
Shibeshi SS, Collins WE (2005) The rheology of blood in a branched arterial system. Appl Rheol 15:398–405
Srivastava LM (1985) Flow of couple stress fluid through stenotic blood vessels. J Biomech 18:479–485
Srivastava N (2014) Analysis of flow characteristics of the blood flowing through an inclined tapered porous artery with mild stenosis under the Influence of an inclined magnetic field. J Biophys 9:797142
Srivastava VP, Rastogi R (2010) Blood flow through a stenosed catheterized artery: effects of hematocrit and stenosis shape. Comput Math Appl 59:1377–1385
Wang K, Mazumdar J, Pincombe B, Worthley SG, Sanders P, Abbot D (2006) Theoretical modeling of micro-scale biological phenomena in human coronary arteries. Med Biol Eng Comput 44:971–982
Whitemore RL (1968) Rheology of circulation. Pergamon Press, Oxford
Wong K, Tu J, Mazumdar J, Abbott D (2010) Modelling of blood flow resistance for an atherosclerotic artery with multiple stenosis and post-stenotic dilations. ANZIAM J 51:66–82
Acknowledgments
The valuable suggestions of the anonymous reviewer are greatly appreciated. The first author Akbar Zaman is grateful to the HEC for financial assistance.
Author information
Authors and Affiliations
Corresponding author
Appendix
Appendix
The explicit numerical scheme which is forward in time and central in space [27] is validated using a variational finite element method (FEM). The finite element method is a powerful technique for solving partial differential equations as well as integral equations and utilizes numerical integration, rather than differentiation as with difference methods. The whole domain is delineated into smaller elements (subdomains) of finite dimensions called “finite elements.” The collection of elements is called the finite element mesh or grid. From the mesh, a typical element is isolated and the variational formulation of the given problem over the typical element is constructed. An approximate solution of the variational problem is assumed, and the element equations are derived by substituting this solution in the governing differential equations. This process generates an element matrix, which is called a stiffness matrix and is constructed by using element interpolation functions. The algebraic equations so obtained are assembled by imposing the inter-element continuity conditions. This yields a large number of algebraic equations defining the global finite element model, which governs the whole domain. The essential and natural boundary conditions are imposed on the assembled equations. The assembled equations so obtained can be solved by any “matrix” numerical technique, e.g., Gaussian elimination method, Householder’s approach and LU Decomposition method, as elaborated by Bathe [6]. Numerous nonlinear micro- and nanoscale biofluid mechanics problems have been successfully addressed in recent years with variational FEM including biomagnetic micropolar convection flow in tissue [2], deoxygenated blood flows [8], pulsating drug dispersion [3], nanobiopolymer manufacture [37] and nanopharmacodynamics [36]. In the present transient problem, the linear momentum Eq. (28) and angular momentum Eq. (29) contain the two dependent variables, w and v, and the independent variables, x and t. Discretization is performed separately in the time domain (t) and in the spatial domain (x). Quadratic elements are used. The variational form associated with Eqs. (28)–(29) over a typical quadratic element is constructed, and arbitrary test functions invoked. Interpolation functions are applied for the dependent variables in the form:
With w 1 = w 2 = Ψ i , i = 1,2. The shape elements for a typical quadratic element (x e , x e+1 ) in the space variable take the form [9]:
Valid for \( x_{e} \le x \le x_{e + 1} \). A similar procedure is used for the time domain. The finite element model of the equations thus formed is given in matrix-vector form by;
Here [K mn] and [δ m] (m, n = 1, 2) are the components of the stiffness matrix and displacement vector and are lengthy integral expressions, which are omitted for conservation of space here. Further details are readily available in the articles of Bég and co-workers [2, 3, 8, 36, 37]. The entire flow domain is divided into 600 quadratic elements. Approximately 1800 linear equations are generated. Following the assembly of all element equations, a large-order matrix is generated. The nonlinear algebraic system of equations is solved iteratively. An accuracy of 0.00001 is used. A convergence criterion based on the relative difference between the current and previous iterations is employed. When these differences reach to desired accuracy, the solution is assumed to have converged and the iterative process is terminated. Two-point Gaussian quadrature is implemented for solving the integrations. The FEM algorithm has been executed in MATLAB running on an Octane SGI desktop workstation and takes 25 s on average. Comparisons of the FEM and FDM solutions are documented in Tables 1, 2 and 3 for axial velocity at two different locations, for both diverging and converging arteries in micropolar blood flow (M ≠ 0). Excellent correlation is obtained testifying to the validity of the FDM computations, the latter which are used in all graphical illustrations.
Rights and permissions
About this article
Cite this article
Zaman, A., Ali, N. & Anwar Bég, O. Numerical simulation of unsteady micropolar hemodynamics in a tapered catheterized artery with a combination of stenosis and aneurysm. Med Biol Eng Comput 54, 1423–1436 (2016). https://doi.org/10.1007/s11517-015-1415-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11517-015-1415-3