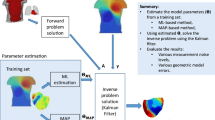
Abstract
In the inverse electrocardiography (ECG) problem, the goal is to reconstruct the heart’s electrical activity from multichannel body surface potentials and a mathematical model of the torso. Over the years, researchers have employed various approaches to solve this ill-posed problem including regularization, optimization, and statistical estimation. It is still a topic of interest especially for researchers and clinicians whose goal is to adopt this technique in clinical applications. Among the wide range of mathematical tools available in the fields of operational research, inverse problems, optimization, and parameter estimation, spline-based techniques have been applied to inverse problems in several areas. If proper spline bases are chosen, the complexity of the problem can be significantly reduced while increasing estimation accuracy. However, there are few studies within the context of the inverse ECG problem that take advantage of this property of the spline-based approaches. In this paper, we evaluate the performance of Multivariate Adaptive Regression Splines (MARS)-based method for the solution of the inverse ECG problem using two different collections of simulated data. The results show that the MARS-based method improves the inverse ECG solutions and is “robust” to modeling errors, especially in terms of localizing the arrhythmia sources.

Multivariate adaptive non-parametric model for inverse ECG problem.













Similar content being viewed by others
References
WHO (2016). Cardiovascular diseases (CVDs), http://www.who.int/mediacentre/factsheets/fs317/en/, [Online, accessed 12.03.2018]
EDGAR. Experimental Data and Geometric Analysis Repository, http://edgar.sci.utah.edu/, [Online, accessed 13.07.2018]
Bayés de Luna A (2014) ECGs for beginners. Wiley, Oxford. https://doi.org/10.1002/9781118821350
Brooks DH, Ahmad GF (1999) Inverse electrocardiography by simultaneous imposition of multiple constraints. IEEE Trans Biomed Eng 46(1):3–18. https://doi.org/10.1109/10.736746
Cluitmans M, Peeters R, Westra R, Volders P (2015) Noninvasive reconstruction of cardiac electrical activity: update on current methods, applications and challenges. Neth Hear J 23(6):301–311. https://doi.org/10.1007/s12471-015-0690-9
Van Oosterom A (2012) The inverse problem of bioelectricity: an evaluation. Med Biol Eng Comput 50 (9):891–902. https://doi.org/10.1007/s11517-012-0941-5
Cluitmans MJM, Bonizzi P, Karel JMH, Das M, Kietselaer BLJH, de Jong MMJ, Volders PGA (2017) In vivo validation of electrocardiographic imaging. JACC: Clinical Electrophysiology 3(3):232–242. https://doi.org/10.1016/j.jacep.2016.11.012
Gulrajani RM (1998) Bioelectricity and Biomagnetism, 1st. Wiley, Oxford
Hansen PC (1998) Rank-deficient and Discrete Ill-posed Problems: Numerical Aspects of Linear Inversion. Philadelphia PA, USA: Society for Industrial and Applied Mathematics
Tikhonov AN, Arsenin VY (1977) Solutions of Ill-Posed problems. Winston and Sons, Washington DC
Serinagaoglu Y, Brooks DH, MacLeod RS (2006) Improved performance of Bayesian solutions for inverse electrocardiography using multiple information sources. IEEE Trans Biomed Eng 53(10):2024–2034
Rudy Y (2013) Noninvasive electrocardiographic imaging of arrhythmogenic substrates in humans. Circ Res 112(5):863–874
CardioInsight (2017). http://www.medtronic.eu/AFS/cardioinsight/index.htm , [Online, accessed 12.03.2018]
Bokeriya LA, Revishvili AS, Kalinin AV, Kalinin VV, Lyadzhina OA, Fetisova EA (2008) Hardware–software system for noninvasive electrocardiographic heart examination based on inverse problem of electrocardiography. Biomed Eng 42(6):273–279. https://doi.org/10.1007/s10527-009-9065-0
AmyCard (2017). http://amycard.com, [Online, accessed 12.03.2018]
Aster RC, Borchers B, Thurber CH (2013) Parameter estimation and inverse problems, 2nd. Academic Press, Boston, pp 355–360
Calvetti D, Morigi S, Reichel L, Sgallari F (2000) Tikhonov regularization and the L-curve for large discrete ill-posed problems. J Comput Appl Math 123:423–446. https://doi.org/10.1016/S0377-0427(00)00414-3
Potyagaylo D, Cortes EG, Schulze WHW, Dossel O (2014) Binary optimization for source localization in the inverse problem of ECG. Med Biol Eng Comput 52(9):717–728. https://doi.org/10.1007/s11517-014-1176-4
Greensite F (2003) The temporal prior in bioelectromagnetic source imaging problems. IEEE Trans Biomed Eng 50(10):1152–1159. https://doi.org/10.1109/TBME.2003.817632
Oster HS, Rudy Y (1992) The use of temporal information in the regularization of the inverse problem of electrocardiography. IEEE Trans Biomed Eng 39(1):65–75. https://doi.org/10.1109/10.108129
Ghodrati A, Brooks DH, Tadmor G, MacLeod RS (2006) Wavefront-based models for inverse electrocardiography. IEEE Trans Biomed Eng 53(9):1821–1831. https://doi.org/10.1109/TBME.2006.878117
Zhang Y, Ghodrati A, Brooks DH (2005) An analytical comparison of three spatio-temporal regularization methods for dynamic linear inverse problems in a common statistical framework. Inverse Prob 21(1):357–382. https://doi.org/10.1088/0266-5611/21/1/022
Greensite F (2002) A new treatment of the inverse problem of multivariate analysis. Inverse Prob 18(2):363. https://doi.org/10.1088/0266-5611/18/2/305
Yao B, Yang H (2016) Physics-driven spatiotemporal regularization for high-dimensional predictive modeling: a novel approach to solve the inverse ECG problem. Sci Report 6(1):39012. https://doi.org/10.1038/srep39012
Gavgani AM, Dogrusoz YS (2011) Use of genetic algorithm for selection of regularization parameters in multiple constraint inverse ECG problem. In: Proceedings of the annual international conference of the IEEE engineering in medicine and biology society. EMBS (3), pp 985–988. https://doi.org/10.1109/IEMBS.2011.6090228
Ghosh S, Rudy Y (2009) Application of L1-Norm regularization to epicardial potential solution of the inverse electrocardiography problem. Ann Biomed Eng 37(5):902–912. https://doi.org/10.1007/s10439-009-9665-6
Xu J, Dehaghani AR, Gao F, Wang L (2014) Noninvasive transmural electrophysiological imaging based on minimization of total-variation functional. IEEE Trans Med Imaging 33(9):1860–1874. https://doi.org/10.1109/TMI.2014.2324900
Wang L, Li X, Chen Y, Qin J (2015) Application of L0-norm regularization to epicardial potential reconstruction. In: MICCAI 2015, Part I, lecture notes in computer science, vol. 9349, pp 493–500
Rahimi A, Xu J, Wang L (2013) Lp norm regularization in volumetric imaging of cardiac current sources. Comput Math Methods Med 2013:1–10. https://doi.org/10.1155/2013/276478
Rahimi A, Sapp J, Xu J, Bajorski P, Horacek M, Wang L (2016) Examining the impact of prior models in transmural electrophysiological imaging: a hierarchical multiple-model bayesian approach. IEEE Trans Med Imaging 35(1):229–243. https://doi.org/10.1109/TMI.2015.2464315
Van Oosterom A (1999) The use of the spatial covariance in computing pericardial potentials. IEEE Trans Biomed Eng 46(7):778–787. https://doi.org/10.1109/10.771187
Onal M, Serinagaoglu Y (2008) Spatio-temporal solutions in inverse electrocardiography. IFMBE Proc 22:180–183
Corrado C, Gerbeau J. -F., Moireau P (2015) Identification of weakly coupled multiphysics problems. Application to the inverse problem of electrocardiography. J Comput Phys 283:271–298. https://doi.org/10.1016/j.jcp.2014.11.041
Aydin U, Dogrusoz YS (2011) A Kalman filter-based approach to reduce the effects of geometric errors and the measurement noise in the inverse ECG problem. Med Biol Eng Comput 49 (9):1003–1013. https://doi.org/10.1007/s11517-011-0757-8
Ghodrati A, Brooks D, Tadmor G, MacLeod R (2006) Wavefront-based models for inverse electrocardiography. IEEE Trans Biomed Eng 53(9):1821–1831. https://doi.org/10.1109/TBME.2006.878117
Babaeizadeh S, Brooks D, Isaacson D (2005) A deformable-radius B-spline method for shape-based inverse problems, as applied to electrical impedance tomography. In: Proceedings. (ICASSP ’05). IEEE international conference on acoustics, speech, and signal processing, 2005, vol. 2, IEEE, pp 485–488. https://doi.org/10.1109/ICASSP.2005.1415447
Miller EL, Kilmer M, Rappaport C (2000) A new shape-based method for object localization and characterization from scattered field data. IEEE Trans Geosci Remote Sens 38(4 I):1682–1696. https://doi.org/10.1109/36.851967
Baussard A, Miller EL, Pr’emel D., Adaptive B (2004) -Spline scheme for solving an inverse scattering problem. Inverse Prob 20(2):347–365. https://doi.org/10.1088/0266-5611/20/2/003
Baussard A, Miller EL, Lesselier D (2004) Adaptive multiscale reconstruction of buried objects. Inverse Prob 20(6):S1–S15. https://doi.org/10.1088/0266-5611/20/6/S01
Zettinig O, Mansi T, Georgescu B, Kayvanpour E, Sedaghat-Hamedani F, Amr A, Haas J, Steen H, Meder B, Katus H, Navab N, Kamen A, Comaniciu D (2013) Fast data-driven calibration of a cardiac electrophysiology model from images and ECG. Lecture Notes in Computer Science (including subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics) 8149 LNCS (PART) 1:1–8
Zettinig O, Mansi T, Neumann D, Georgescu B, Rapaka S, Seegerer P, Kayvanpour E, Sedaghat-Hamedani F, Amr A, Haas J, Steen H, Katus H, Meder B, Navab N, Kamen A, Comaniciu D (2014) Data-driven estimation of cardiac electrical diffusivity from 12-lead ECG signals. Med Image Anal 18(8):1361–1376. https://doi.org/10.1016/j.media.2014.04.011
Erem B, Coll-Font J, Orellana RM, St’Ovicek P, Brooks DH (2014) Using transmural regularization and dynamic modeling for noninvasive cardiac potential imaging of endocardial pacing with imprecise thoracic geometry. IEEE Trans Med Imaging 33(3):726–738. https://doi.org/10.1109/TMI.2013.2295220
Harmening C, Neuner H (2016) Choosing the optimal number of b-spline control points (part 1: methodology and approximation of curves). J Appl Geodesy 10:139–157. https://doi.org/10.1515/jag-2016-0003
Härdle W (1994) Applied nonparametric regression. Cambridge University Press, New York
Faraway JJ (1994) Extending the linear model with r: generalized linear, mixed effects and nonparametric regression models, 2nd. Chapman & Hall/CRC, Boca Raton
Boor CD (2001) A practical guide to splines (Revised Edition), vol 27, 1st edn. Springer, New York
Özmen A., Weber G, Batmaz I, Kropat E (2011) RCMARS: Robustification Of CMARS with different scenarios under polyhedral uncertainty set. Commun Nonlinear Sci Numer Simul 16:4780–4787. https://doi.org/10.1016/j.cnsns.2011.04.001
Weber G-W, Batmaz N, Köksal G, Taylan P, Yerlikaya-Özkurt F (2012) CMARS: a new contribution to nonparametric regression with multivariate adaptive regression splines supported by continuous optimization, Inverse Problems in Science and Engineering 20(3):371–400. https://doi.org/10.1080/17415977.2011.624770
Kuter S, Weber GW, Özmen A, Akyürek Z (2014) Modern applied mathematics for alternative modeling of the atmospheric effects on satellite images. In: Modeling, dynamics, optimization and Bioeconomics I. Springer, pp 469–485
Kuter S, Weber G-W, Akyürek Z, Özmen A. (2015) Inversion of top of atmospheric reflectance values by conic multivariate adaptive regression splines. Inverse Prob Sci Eng 23(4):651–669. https://doi.org/10.1080/17415977.2014.933828
Özmen A, Batmaz İ, Weber GW (2014) Precipitation modeling by polyhedral RCMARS and comparison with MARS and CMARS. Environ Model Assess 19(5):425–435. https://doi.org/10.1007/s10666-014-9404-8
Yerlikaya-Özkurt F, Askan A, Weber G-W (2014) An alternative approach to the ground motion prediction problem by a non-parametric adaptive regression method. Eng Optim 46(12):1651–1668. https://doi.org/10.1080/0305215X.2013.858141
Zhang W, Goh AT (2016) Multivariate adaptive regression splines and neural network models for prediction of pile drivability. Geosci Front 7(1):45–52. https://doi.org/10.1016/j.gsf.2014.10.003
Ayyildiz E, Purutçuoğlu V, Weber GW (2017) Loop-based conic multivariate adaptive regression splines is a novel method for advanced construction of complex biological networks. Eur J Oper Res 270(1):852–861. https://doi.org/10.1016/j.ejor.2017.12.011
Çevik A, Weber G-W, Eyu̧boğlu BM, Oğuz KK (2017) Voxel-MARS: a method for early detection of Alzheimer’s disease by classification of structural brain MRI. Ann Oper Res 258(1):31–57. https://doi.org/10.1007/s10479-017-2405-7
Özmen A, Weber G-W (2018) Natural gas consumption forecast with MARS and CMARS models for residential users. Energy Econ 70:357–381. https://doi.org/10.1016/j.eneco.2018.01.022
Jekabsons G (2016). ARESLab: Adaptive Regression Splines toolbox, http://www.cs.rtu.lv/jekabsons/regression.html, [Online, accessed 12.03.2018]
Twomey S (1963) On the numerical solution of fredholm integral equations of the first kind by the inversion of the linear system produced by quadrature. J ACM 10(1):97–101. https://doi.org/10.1145/321150.321157
Friedman JH (1991) Multivariate adaptive regression splines. Ann Stat 19(1):1–67. https://doi.org/10.1214/aos/1176347963
Friedman JH, Roosen CB (1995) An introduction to multivariate adaptive regression splines. Stat Methods Med Res 4(3):197–217. https://doi.org/10.1177/096228029500400303
Taylan P, Weber G-W, Yerlikaya Özkurt F (2010) A new approach to multivariate adaptive regression splines by using Tikhonov regularization and continuous optimization. TOP 18(2):377–395. https://doi.org/10.1007/s11750-010-0155-7
MacLeod R, Taccardi B, Lux R (1995) Electrocardiographic mapping in a realistic torso tank preparation. In: Proceedings of 17th international conference of the engineering in medicine and biology society, vol. 1. IEEE, pp 245–246. https://doi.org/10.1109/IEMBS.1995.575092
Lux RL, Smith CR, Wyatt RF, Abildskov JA (1978) Limited lead selection for estimation of body surface potential maps in electrocardiography. IEEE Trans Biomed Eng 25(3):270–6. https://doi.org/10.1109/TBME.1978.326332
Stanley PC, Pilkington TC, Morrow MN (1986) The effects of thoracic inhomogeneities on the relationship between epicardial and torso potentials. IEEE Trans Biomed Eng 33(3):273–284. https://doi.org/10.1109/TBME.1986.325711
Ramanathan C, Rudy Y (2001) Electrocardiographic imaging: I. effect of torso inhomogeneities on body surface electrocardiographic potentials. J Cardiovasc Electrophysiol 12(2):229–240. https://doi.org/10.1046/j.1540-8167.2001.00229.x
Klepfer RN, Johnson CR, Macleod RS (1997) The effects of inhomogeneities and anisotropies on electrocardiographic fields: a 3-D finite-element study. IEEE Trans Biomed Eng 44(8):706–719. https://doi.org/10.1109/10.605427
MacLeod R, Johnson C (1993) Map3d: interactive scientific visualization for bioengineering data. In: Proceedings of the 15th annual international conference of the ieee engineering in medicine and biology societ. IEEE, pp 30–31. https://doi.org/10.1109/IEMBS.1993.978414
Han C, Liu Z, Zhang X, Pogwizd S, He B (2008) Noninvasive three-dimensional cardiac activation imaging from body surface potential maps: a computational and experimental study on a rabbit model. IEEE Trans Med Imaging 27(11):1622–1630. https://doi.org/10.1109/TMI.2008.929094
Bear LR, Huntjens PR, Walton RD, Bernus O, Coronel R, Dubois R (2018) Cardiac electrical dyssynchrony is accurately detected by noninvasive electrocardiographic imaging. Heart Rhythm 15(7):1058–1069. https://doi.org/10.1016/j.hrthm.2018.02.024
Messinger-Rapport BJ, Rudy Y (1986) The inverse problem in electrocardiography: a model study of the effects of geometry and conductivity parameters on the reconstruction of epicardial potentials. IEEE Trans Biomed Eng BME-33(7):667–676. https://doi.org/10.1109/TBME.1986.325756
Huiskamp GJ, van Oosterom A (1989) Tailored versus realistic geometry in the inverse problem of electrocardiography. IEEE Trans Biomed Eng 36(8):827–35. https://doi.org/10.1109/10.30808
Throne RD, Olson LG (1995) The effects of errors in assumed conductivities and geometry on numerical solutions to the inverse problem of electrocardiography. IEEE Trans Biomed Eng 42(12):1192–1200. https://doi.org/10.1109/10.476126
Schulze WHW, Potyagaylo D, Schimpf R, Papavassiliu T, Tulumen E, Rudic B, Dössel O (2015) A simulation dataset for ECG imaging of paced beats with models for transmural, endo- and epicardial and pericardial source imaging, (November), 1–6. https://doi.org/10.13140/RG.2.1.1946.8568
Acknowledgments
The authors would like to thank Dr. Robert S. MacLeod from University of Utah, Nora Eccles Harrison Cardiovascular Research and Training Institute for the data used in this study. The qualitative assessments in this work became possible by software, Map3d, which was supported by the National Institute of General Medical Sciences of the National Institutes of Health under grant number P41 GM103545-18. The authors also would like to thank Karlsruhe Institute of Technology (KIT) and Walther H. W. Schulze and his colleagues for the data used in this study, and the Consortium of ECGI for facilitating data sharing for all researchers.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Onak, Ö.N., Dogrusoz, Y.S. & Weber, G.W. Evaluation of multivariate adaptive non-parametric reduced-order model for solving the inverse electrocardiography problem: a simulation study. Med Biol Eng Comput 57, 967–993 (2019). https://doi.org/10.1007/s11517-018-1934-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11517-018-1934-9