Abstract
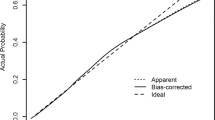
Appropriate management of hypertensive patients relies on the accurate identification of clinically relevant features. However, traditional statistical methods may ignore important information in datasets or overlook possible interactions among features. Machine learning may improve the prediction accuracy and interpretability of regression models by identifying the most relevant features in hypertensive patients. We sought the most relevant features for prediction of cardiovascular (CV) events in a hypertensive population. We used the penalized regression models least absolute shrinkage and selection operator (LASSO) and elastic net (EN) to obtain the most parsimonious and accurate models. The clinical parameters and laboratory biomarkers were collected from the clinical records of 1,471 patients receiving care at Mostoles University Hospital. The outcome was the development of major adverse CV events. Cox proportional hazards regression was performed alone and with penalized regression analyses (LASSO and EN), producing three models. The modeling was performed using 10-fold cross-validation to fit the penalized models. The three predictive models were compared and statistically analyzed to assess their classification accuracy, sensitivity, specificity, discriminative power, and calibration accuracy. The standard Cox model identified five relevant features, while LASSO and EN identified only three (age, LDL cholesterol, and kidney function). The accuracies of the models (prediction vs. observation) were 0.767 (Cox model), 0.754 (LASSO), and 0.764 (EN), and the areas under the curve were 0.694, 0.670, and 0.673, respectively. However, pairwise comparison of performance yielded no statistically significant differences. All three calibration curves showed close agreement between the predicted and observed probabilities of the development of a CV event. Although the performance was similar for all three models, both penalized regression analyses produced models with good fit and fewer features than the Cox regression predictive model but with the same accuracy. This case study of predictive models using penalized regression analyses shows that penalized regularization techniques can provide predictive models for CV risk assessment that are parsimonious, highly interpretable, and generalizable and that have good fit. For clinicians, a parsimonious model can be useful where available data are limited, as such a model can offer a simple but efficient way to model the impact of the different features on the prediction of CV events. Management of these features may lower the risk for a CV event.

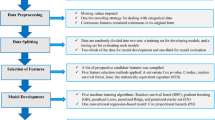
In a clinical setting, with numerous biological and laboratory features and incomplete datasets, traditional statistical methods may ignore important information and overlook possible interactions among features. Our aim was to identify the most relevant features to predict cardiovascular events in a hypertensive population, using three different regression approaches for feature selection, to improve the prediction accuracy and interpretability of regression models by identifying the relevant features in these patients.





Similar content being viewed by others
References
Lackland DT, Weber MA (2015) Global burden of cardiovascular disease and stroke: hypertension at the core. Can J Cardiol 31(5):569–571
Perkovic V, Huxley R, Wu Y, Prabhakaran D, MacMahon S (2007) The burden of blood pressure-related disease: a neglected priority for global health. Hypertension (Dallas, Tex : 1979) 50(6):991–997
Lackland DT, Roccella EJ, Deutsch AF, Fornage M, George MG, Howard G, Kissela BM, Kittner SJ, Lichtman JH, Lisabeth LD et al (2014) Factors influencing the decline in stroke mortality: a statement from the american heart association/american stroke association. Stroke 45(1):315–353
Long AN, Dagogo-Jack S (2011) Comorbidities of diabetes and hypertension: mechanisms and approach to target organ protection. J Clin Hypertens 13(4):244–251
Noh J, Kim HC, Shin A, Yeom H, Jang S-Y, Lee JH, Kim C, Suh I (2016) Prevalence of comorbidity among people with hypertension: the Korea national health and nutrition examination survey 2007-2013. Korean Circulation Journal 46(5):672– 680
Grover SA, Hemmelgarn B, Joseph L, Milot A, Tremblay G (2006) The role of global risk assessment in hypertension therapy. Can J Cardiol 22(7):606–613
Clark TG, Bradburn MJ, Love SB, Altman DG (2003) Survival analysis part I: basic concepts and first analyses. Br J Cancer 89(2):232–238
Cox DR (1992) Regression models and life-tables. In: Breakthroughs in statistics. Springer, pp 527–541
Pavlou M, Ambler G, Seaman SR, Guttmann O, Elliott P, King M, Omar RZ (2015) How to develop a more accurate risk prediction model when there are few events. BMJ (Clinical research ed.) 351:h3868
Schisterman EF, Perkins NJ, Mumford SL, Ahrens KA, Mitchell EM (2017) Collinearity and causal diagrams: a lesson on the importance of model specification. Epidemiology (Cambridge, Mass) 28(1):47–53
Weng SF, Reps J, Kai J, Garibaldi JM, Qureshi N (2017) Can machine-learning improve cardiovascular risk prediction using routine clinical data? PLoS One 12(4):e0174944
Goldstein BA, Navar AM, Carter RE (2016) Moving beyond regression techniques in cardiovascular risk prediction: applying machine learning to address analytic challenges. Eur Heart J 38(23):1805–1814
Ambale-Venkatesh B, Yang X, Wu CO, Liu K, Hundley WG, McClelland R, Gomes AS, Folsom AR, Shea S, Guallar E et al (2017) Cardiovascular event prediction by machine learning: the multi-ethnic study of atherosclerosis. Circ Res 121(9):1092– 1101
Collins GS, Reitsma JB, Altman DG, Moons KGM (2015) Transparent reporting of a multivariable prediction model for individual prognosis or diagnosis (TRIPOD): the TRIPOD statement. BMC Medicine 13(1):1
Neumaier A (1998) Solving Ill-conditioned and singular linear systems: a tutorial on regularization. SIAM Rev 40(3):636–666
Tibshirani R (1996) Regression shrinkage and selection via the Lasso. J R Stat Soc Ser B Methodol 58 (1):267– 288
Tibshirani R (1997) The lasso method for variable selection in the cox model. Stat Med 16(4):385–395
Pavlou M, Ambler G, Seaman SR, Guttmann O, Elliott P, King M, Omar RZ (2015) How to develop a more accurate risk prediction model when there are few events. Bmj 351:h3868
Friedman J, Hastie T, Tibshirani R (2010) Regularization paths for generalized linear models via coordinate descent. J Stat Softw, Articles 33(1):1–22
Zou H, Hastie T (2005) Regularization and variable selection via the elastic net. J R Stat Soc Ser B Stat Methodol 67(2):301–320
Simon N, Friedman J, Hastie T, Tibshirani R (2011) Regularization paths for Cox’s proportional hazards model via coordinate descent. J Stat Softw 39(5):1–13
Garcia-Carretero R, Vigil-Medina L, Barquero-Perez O, Goya-Esteban R, Mora-Jimenez I, Soguero-Ruiz C, Ramos-Lopez J (2017) Cystatin c as a predictor of cardiovascular outcomes in a hypertensive population. J Hum Hypertens 31(12):801
Levey AS, Stevens LA, Schmid CH, Zhang YL, Castro AF, Feldman HI, Kusek JW, Eggers P, Van Lente F, Greene T et al (2009) A new equation to estimate glomerular filtration rate. Ann Inter Med 150(9):604–612
Inker LA, Schmid CH, Tighiouart H, Eckfeldt JH, Feldman HI, Greene T, Kusek JW, Manzi J, Van Lente F, Zhang YL et al (2012) Estimating glomerular filtration rate from serum creatinine and cystatin c. N Engl J Med 367(1):20–29
R Core Team (2017) R: a language and environment for statistical computing
Uno H, Cai T, Pencina MJ, D’Agostino RB, Wei LJ (2011) On the c-statistics for evaluating overall adequacy of risk prediction procedures with censored survival data. Stat Med 30(10):1105–1117
Steyerberg EW, Vickers AJ, Cook NR, Gerds T, Gonen M, Obuchowski N, Pencina MJ, Kattan MW (2010) Assessing the performance of prediction models: a framework for some traditional and novel measures. Epidemiology (Cambridge, Mass) 21(1):128–138
Grimes DA (2008) The nomogram epidemic: resurgence of a medical relic. Ann Inter Med 149(4):273–275
Balachandran VP, Gonen M, Smith JJ, DeMatteo RP (2015) Nomograms in oncology: more than meets the eye. Lancet Oncol 16(4):e173—e180
Friedman J, Hastie T, Tibshirani R (2009) The elements of statistical learning, vol 1. Springer series in statistics, New York
DeLong ER, DeLong DM, Clarke-Pearson DL (1988) Comparing the areas under two or more correlated receiver operating characteristic curves: a nonparametric approach. Biometrics 44(3):837–845
Yue Y, Osipov A, Fraass B, Sandler H, Zhang X, Nissen N, Hendifar A, Tuli R (2017) Identifying prognostic intratumor heterogeneity using pre- and post-radiotherapy 18F-FDG PET images for pancreatic cancer patients. Journal of Gastrointestinal Oncology 8(1):127–138
Lu M, Zhou J, Naylor C, Kirkpatrick BD, Haque R, Petri WA Jr, Ma JZ (2017) Application of penalized linear regression methods to the selection of environmental enteropathy biomarkers. Biol Res 5:9
A LASSO penalized regression approach for genome-wide association analyses using related individuals: application to the Genetic Analysis Workshop 19 simulated data.BMC proceedings, 10(Suppl 7):221–226 (2016)
Suchting R, Hebert ET, Ma P, Kendzor DE, Businelle MS (2017) Using elastic net penalized cox proportional hazards regression to identify predictors of imminent smoking lapse. Nicotine & tobacco research : official journal of the Society for Research on Nicotine and Tobacco, sep 2017
Ambler G, Seaman S, Omar RZ (2012) An evaluation of penalised survival methods for developing prognostic models with rare events. Stat Med 31(11-12):1150–1161
Genell A, Nemes S, Steineck G, Dickman PW (2010) Model selection in medical research: a simulation study comparing Bayesian model averaging and stepwise regression. BMC Med Res Method 10:108
Hancock AA, Bush EN, Stanisic D, Kyncl JJ, Lin CT (1988) Data normalization before statistical analysis: keeping the horse before the cart. Trends Pharmacol Sci 9(1):29– 32
Lloyd-Jones DM, Leip EP, Larson MG, d’Agostino RB, Beiser A, Wilson PW, Wolf PA, Levy D (2006) Prediction of lifetime risk for cardiovascular disease by risk factor burden at 50 years of age. Circulation 113(6):791–798
Lloyd-Jones DM, Larson MG, Beiser A, Levy D (1999) Lifetime risk of developing coronary heart disease. The Lancet 353(9147):89–92
Seshadri S, Beiser A, Kelly-Hayes M, Kase CS, Au R, Kannel WB, Wolf PA (2006) The lifetime risk of stroke: estimates from the Framingham study. Stroke 37(2):345–350
Lloyd-Jones DM, Larson MG, Leip EP, Beiser A, D’Agostino RB, Kannel WB, Murabito JM, Vasan RS, Benjamin EJ, Levy D (2002) Lifetime risk for developing congestive heart failure: the Framingham heart study. Circulation 106(24):3068– 3072
Sniderman AD, Furberg CD (2008) Age as a modifiable risk factor for cardiovascular disease. The Lancet 371(9623):1547– 1549
Dhingra R, Vasan RS (2012) Age as a risk factor. Med Clin 96(1):87–91
Funding
This work was partly funded by Research Projects TEC2016-75361-R and TEC2016-75161-C2-1-R of the Spanish Government and Research Project DTS17/00158 from Instituto Carlos III (Spain).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interests
The authors declare that they have no conflicts of interest.
Ethical approval
All procedures performed in studies involving human participants were in accordance with the ethical standards of the institutional and national research committees, as well as with the 1964 Helsinki Declaration and its later amendments or comparable ethical standards.
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Garcia-Carretero, R., Barquero-Perez, O., Mora-Jimenez, I. et al. Identification of clinically relevant features in hypertensive patients using penalized regression: a case study of cardiovascular events. Med Biol Eng Comput 57, 2011–2026 (2019). https://doi.org/10.1007/s11517-019-02007-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11517-019-02007-9