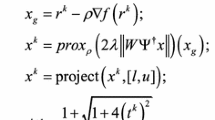Abstract
To reduce the magnetic resonance imaging (MRI) data acquisition time and improve the MR image reconstruction performance, reconstruction algorithms based on the iterative shrinkage thresholding algorithm (ISTA) are widely used. However, these traditional algorithms use global threshold shrinkage, which is not efficient. In this paper, a novel algorithm based on local threshold shrinkage, which is called the local shrinkage thresholding algorithm (LSTA), was proposed. The LSTA can shrink differently for different elements from the residual matrix to adjust the shrinkage speed for each element of the image during the iterative process. Then, by taking advantage of the sparser characteristics of the curvelet transform, the LSTA combined with the curvelet transform (CLSTA) can make the construction process more efficient. Finally, compared with ISTA, the generalized thresholding iterative algorithm (GTIA) and the fast iterative shrinkage threshold algorithm (FISTA), when analysing human (brain and cervical) MR images, a conclusion can be drawn that the proposed method has better reconstruction performance in terms of the mean square error (MSE), the peak signal to noise ratio (PNSR), the structural similarity index measure (SSIM), the normalized mutual information (NMI), the transferred edge information (TEI) and the number of iterations. The proposed method can better maintain the detailed information of the reconstructed images and effectively decrease the blurring of the images edges.

Graphical abstract








Similar content being viewed by others
References
Wright GA (1997) Magnetic resonance imaging[J]. Signal Process Mag IEEE 14(1):56–66
Balestreri L (2012) Computed tomography: fundamentals, system technology, image performance, applications, 2nd edition[J]. Clin Imaging 53(8):218
Donoho DL (2006) Compressed sensing[J]. IEEE Trans Inf Theory 52(4):1289–1306
Beck A, Teboulle M (2009) A fast iterative shrinkage-thresholding algorithm for linear inverse problems[J]. Siam Journal on Imaging Sciences 2(1):183–202
Goldstein T, Osher S (2009) The Split Bregman method for L1-regularized problems[M]. Soc Ind Appl Math
Luo J, Mou Z, Qin B et al (2017) A singular K-space model for fast reconstruction of magnetic resonance images from undersampled data[J]. Med Biol Eng Comput (6):1–15
Qu X, Zhang W, Guo D, Cai C, Cai S, Chen Z (2010) Iterative thresholding compressed sensing MRI based on contourlet transform[J]. Inverse Prob Sci Eng 18(6):737–758
Bioucasdias JM, Figueiredo MAT (2007) A new TwIST: two-step iterative shrinkage/thresholding algorithms for image restoration[J]. IEEE Transactions on Image Processing A Publication of the IEEE Signal Processing Society 16(12):2992–3004
Elahi S, Kaleem M, Omer H (2018) Compressively sampled MR image reconstruction using generalized thresholding iterative algorithm[J]. J Magn Reson 286:91–98
Muckley MJ, Noll DC, Fessler JA (2015) Fast parallel MR image reconstruction via B1-based, adaptive restart, iterative soft thresholding algorithms (BARISTA)[J]. IEEE Trans Med Imaging 34(2):578–588
Starck J, Donoho DL, Candès EJ (2002) The curvelet transform for image denoising[J]. IEEE Transactions on Image Processing 11(6):670–684
Candes E, Demanet L, Donoho D et al (2006) Fast discrete curvelet transforms[J]. Multiscale Model Simul 5(3):861–899
Long TJ (1982) Strong nondeterministic polynomial-time reducibilities[J]. Theor Comput Sci 21(1):1–25
Zhang H, Yin W, Cheng L (2015) Necessary and sufficient conditions of solution uniqueness in 1-norm minimization[J]. J Optim Theory Appl 164(1):109–122
Lustig M, Donoho DJ, Sparse MRI (2010) The application of compressed sensing for rapid MR imaging[J]. Magn Reson Med 58(6):1182–1195
Wang Y, Lian QS, Li K (2010) MRI reconstruction based on compound regularizers and compressed sensing[J]. Optical Technique 36(3):350–355
Jiao LC, Tan S, Liu F (2005) Ridgelet theory: from Ridgelet transform to curvelet[J]. Chinese Journal of Engineering Mathematics 22(5):761–773
Hammouche AM, El-Bakry HM, Mostafa RR (2016) Image contrast enhancement using fast discrete curvelet transform via unequally spaced fast Fourier transform (FDCT-USFFT) [J]. International Journal of Electronics Communication and Computer Engineering 7(2):88–93
Tan H, Meyer CH (2009) Estimation of k-space trajectories in spiral MRI[J]. Magn Reson Med 61(6):1396–1404
Ravishankar S, Bresler Y (2011) MR image reconstruction from highly under sampled k-space data by dictionary learning[J]. IEEE Trans Med Imaging 30(5):1028–1041
Al-Najjar Y (2012) Comparison of image performance assessment: PSNR, HVS, SSIM, UIQI[J]. Int J Sci Eng Res 3:3
Wang Z, Bovik AC, Sheikh HR, Simoncelli EP (2004) Image performance assessment: from error visibility to structural similarity[J]. IEEE Trans Image Process 13(4):600–612
Funding
This work was supported by the National Natural Science Foundation of China (81701806), the National Natural Science Foundation of China (81601612), Key Medical Subjects of Jiangsu Province (BE 2015613, BE 2016763) and the Co-innovation Foundation of NMU and SEU (2017DN31).
Author information
Authors and Affiliations
Corresponding authors
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Wang, H., Zhou, Y., Wu, X. et al. Reconstruction of compressively sampled MR images based on a local shrinkage thresholding algorithm with curvelet transform. Med Biol Eng Comput 57, 2145–2158 (2019). https://doi.org/10.1007/s11517-019-02017-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11517-019-02017-7