Airway performance in infants with congenital tracheal stenosis associated with unilateral pulmonary agenesis: effect of tracheal shape on energy flux

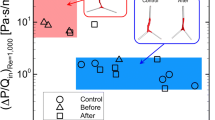
Abstract

Congenital tracheal stenosis (CTS) with unilateral pulmonary agenesis (UPA) is characterized by the absence of one or both lungs in the hemithorax and is often associated with airway distortion. Some UPA patients have high mortality and morbidity even postoperatively, and it remains unclear whether surgery increases the energy flux needed to drive airflow. Here, we used pre- and postoperative patient-specific airway models to numerically investigate tracheal flow in patients with CTS, especially flow associated with right UPA (CTS-RUPA). Airflow was simulated with the large-eddy model, and energy flux was investigated to quantify airway performance and the contribution of surgical intervention. Although energy flux decreased postoperatively, clinical respiratory status did not improve. Standard surgical intervention for CTS, which expands the minimal cross-sectional area, decreased energy flux, i.e., improved airway performance. The simulation also included artificial airways with a straightened bend or reduced tracheal lumen roughness. The numerical results clearly showed interindividual differences in the percent reduction of energy flux caused by straightening the tracheal bend versus correcting tracheal lumen roughness. Although this study was limited to small sample size, these numerical results indicated that energy flux alone is insufficient to evaluate breathing performance in patients with CTS-RUPA but it can be used to estimate airway performance.

Graphical abstract

Appendices

Appendix

Airflows in RUPA and normal subjects

We preliminarily checked the difference in energy flux E_T obtained with the LES, realizable k-ε, and SST k-ω turbulence models. Figure  

Fig. 7

a Airway models for patient P6 before and after surgery (left and right, respectively; straight tubes at the inlet/outlet are not shown); this patient was diagnosed with right lung agenesis without CTS. The models are not to scale and are also rotated for illustrative purposes. b The cross-sectional area A of the trachea is shown as a function of the distance from the inlet of the real airway both preoperatively (solid black line) and postoperatively (solid red line). c Comparison of energy flux E_T in P6 before and after surgery, obtained with different turbulence models: LES, realizable k-ε, and k-ω SST models

7 shows the calculated E_T obtained with these models before and after surgery in a patient (P6) diagnosed with right lung agenesis without CTS, i.e., tracheal cartilage rings were the same as those in healthy subjects. Since P6 was not diagnosed with CTS, the data was not included in the aforementioned results for 5 patients (P1–P5). Although we could not find significant differences in E_T among the three models at least in this patient, all simulations in this study were performed using the LES model, which is higher fidelity than the other two models. Note that P6 was in good prognosis and did not undergo repeat surgery.

Instead of model validation using, e.g., a lung phantom or microfluidics, we further simulated airflows in five healthy controls (C1–C5) with an average age of seven months. The definition of the target area was from just under the larynx to just below the tracheal bifurcation, with a length of approximately 45–60 mm. One of five normal airway models was shown in Fig. 

Fig. 8

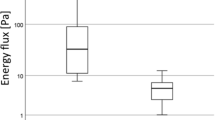
a One of the normal subject airway models (C1–C5). Straight tubes are attached to the inlet and two outlets of real airways, which are colored red. b The energy flux E_T is shown as box plots (five normal subjects, five preoperative patients, and four postoperative patients). The data of each subject are displayed as circles. c E_T as a function of the minimum cross-sectional area A_min. The results of five normal controls and P6 were also displayed. The dashed line is the approximation curve same as in Fig. 4b, where data of P1–P5 was only used

8a, where straight tubes with 50 mm length to the inlet and two outlets of real airways were also visualized. Even though normal subject airway models include carina, the median value of E_T (90.6 Pa) in healthy controls was smaller than those in CTS-RUPA (140.8 Pa) as shown in Fig. 8b. The result may indicate that the airway performance of preoperative patients with CTS-RUPA is lower than or almost the same as that of healthy subjects. The relationship between E_T and A_min for P6 and five healthy controls were added in Fig. 4b, and the results were summarized in Fig. 8c. Although E_T in five controls was well approximated by data of P1–P5, E_T in P6^Aft was far away from the approximation curve (Fig. 8c). Considering this numerical result and good prognosis of P6, clinical respiratory status in patients with RUPA may be different from those in patients with CTS-RUPA. Further statistical analysis is required, which is however our future study.

Realizable k-ε and SST k-ω turbulence

Governing equations of realizable k-ε and shear stress transport (SST) k-ω turbulence models were described below. The 3D steady Reynolds averaged Navier–Stokes (RANS) equations were commonly considered in those models. Substituting mean and fluctuating components of the flow into an incompressible Navier–Stokes equation, continuity and RANS equations are written as

$$\frac{{\partial \overline{u}_{i} }}{{\partial x_{i} }} = 0,$$

(3)

$$\frac{{\partial \overline{u}_{i} }}{\partial t} + \frac{{\partial \left( {\overline{u}_{i} \overline{u}_{j} } \right)}}{{\partial x_{j} }} = - \frac{1}{p}\frac{{\partial \overline{p} }}{{\partial x_{i} }} + \frac{\partial }{{\partial x_{j} }}\left( {2\nu \overline{D}_{ij} - \overline{{u_{i}^{\prime } u_{j}^{\prime } }} } \right),$$

(4)

where ${\overline{u} }_{i}$ and ${u}_{i}$ are the mean and fluctuating velocities, $\overline{p }$ is the mean pressure, and ${\overline{D} }_{ij}$ is a strain-rate tensor, which is given by

$$\overline{D}_{ij} = \frac{1}{2}\left( {\frac{{\partial \overline{u}_{i} }}{{\partial x_{j} }} + \frac{{\partial \overline{u}_{j} }}{{\partial x_{i} }}} \right).$$

(5)

The standard eddy viscosity formulation for incompressible turbulence is

$$\overline{{u_{i}^{\prime } u_{j}^{\prime } }} = - 2\nu_{t} \overline{D}_{ij} + \frac{2}{3}k\delta_{ij} ,$$

(6)

$$\nu_{t} = C_{\mu } \frac{{k^{2} }}{\varepsilon }.$$

(7)

For the realizable k-ε turbulence model, the turbulent kinetic energy k and its rate of dissipation ε come directly from their differential transport equations:

$$\frac{\partial k}{{\partial t}} + \frac{{\partial k\overline{u}_{j} }}{{\partial x_{j} }} = P_{k} - \varepsilon + \frac{\partial }{{\partial x_{j} }}\left\{ {\left( {\nu + \frac{{\nu_{T} }}{{\sigma_{k} }}} \right)\frac{\partial k}{{\partial x_{j} }}} \right\},$$

(8)

$$\frac{\partial \varepsilon }{{\partial t}} + \frac{{\partial \varepsilon \overline{u}_{j} }}{{\partial x_{j} }} = \frac{\varepsilon }{k}C_{\varepsilon 1} P_{k} - C_{\varepsilon 2} \frac{{\varepsilon^{2} }}{{k + \sqrt {\nu \varepsilon } }} + \frac{\partial }{{\partial x_{j} }}\left\{ {\left( {\nu + \frac{{\nu_{T} }}{{\sigma_{\varepsilon } }}} \right)\frac{\partial \varepsilon }{{\partial x_{j} }}} \right\},$$

(9)

and

$$P_{k} = - \overline{{u_{i}^{\prime } u_{j}^{\prime } }} \frac{{\partial \overline{u}_{i} }}{{\partial x_{j} }} = 2\nu_{T} \overline{D}_{ij} \overline{D}_{ij} ,$$

(10)

where σ_k and σ_ε are the turbulent Prandtl number for k and ε, respectively. C_ε1, C_µ and A_s were computed by:

$$C_{{\varepsilon_{1} }} = \max \left( {0.43,\frac{\eta }{5 + \eta }} \right),\quad \eta = \frac{k}{\varepsilon }\sqrt {2\overline{D}_{ij} \overline{D}_{ij} } ,$$

(11)

$$C_{\mu } = \frac{1}{{A_{0} + A_{s} {\mathcal{U}}^{*} k/\varepsilon }},\quad {\mathcal{U}}^{*} = \sqrt {\overline{D}_{ij} \overline{D}_{ij} + \overline{\Omega }_{ij} \overline{\Omega }_{ij} } ,\quad \overline{\Omega }_{ij} = \frac{1}{2}\left( {\frac{{\partial \overline{u}_{i} }}{{\partial x_{j} }} - \frac{{\partial \overline{u}_{j} }}{{\partial x_{i} }}} \right),$$

(12)

$$A_{s} = \sqrt 6 \cos \phi ,\quad \phi = \frac{1}{3}\arccos \sqrt 6 W,\quad W = \max \left[ { - \frac{1}{\sqrt 6 },\min \left( {\frac{{\overline{D}_{ij} \overline{D}_{jk} \overline{D}_{ki} }}{{\left( {\overline{D}_{ij} \overline{D}_{ij} } \right)^{3/2} }},\frac{1}{\sqrt 6 }} \right)} \right].$$

(13)

The other constants (${\sigma }_{k}$, ${\sigma }_{\varepsilon }$, ${C}_{\varepsilon 2}$, ${A}_O$) are determined as ${\sigma }_{k}=1.0$, ${\sigma }_{\varepsilon }=1.2$, ${C}_{\varepsilon 2}=1.9$, ${A}_{O}=4.0$ [31]. More precise descriptions about realizable $k-\varepsilon$ turbulence model should be referred to [31, 32].

In SST $k-\omega$ turbulence model, the turbulent kinetic energy k and specific dissipation rate $\omega (=\varepsilon /k)$ are written as

$$\frac{\partial k}{{\partial t}} + \frac{{\partial k\overline{u}_{j} }}{{\partial x_{j} }} = \widetilde{P}_{k} - \beta^{*} k\omega + \frac{\partial }{{\partial x_{j} }}\left\{ {\left( {\nu + \sigma_{k} \nu_{T} } \right)\frac{\partial k}{{\partial x_{j} }}} \right\},$$

(14)

$$\frac{\partial \omega }{{\partial t}} + \frac{{\partial \omega \overline{u}_{j} }}{{\partial x_{j} }} = \frac{\gamma }{{\nu_{T} }}P_{k} - \beta \omega^{2} + \frac{\partial }{{\partial x_{j} }}\left\{ {\left( {\nu + \sigma_{\omega } \nu_{T} } \right)\frac{\partial \varepsilon }{{\partial x_{j} }}} \right\} + 2\left( {1 - F_{1} } \right)\sigma_{\omega 2} \frac{1}{\omega }\frac{\partial k}{{\partial x_{j} }}\frac{\partial \omega }{{\partial x_{j} }},$$

(15)

and

$$\widetilde{P}_{k} = \min \left( {P_{k} ,10\beta^{*} k\omega } \right),$$

(16)

$$F_{1} = \tanh \left\{ {\left\{ {\min \left[ {\max \left( {\frac{\sqrt k }{{\beta^{*} \omega y}},\frac{500\nu }{{y^{2} \omega }}} \right),\frac{{4\sigma_{\omega 2} k}}{{CD_{k\omega } y^{2} }}} \right]} \right\}^{4} } \right\},\quad CD_{k\omega } = \max \left( {\frac{{2\sigma_{\omega 2} }}{\omega }\frac{\partial k}{{\partial x_{j} }}\frac{\partial \omega }{{\partial x_{j} }},10^{ - 10} } \right),$$

(17)

$$\nu_{T} = \frac{{\alpha_{1} k}}{{\max \left( {\alpha_{1} \omega ,F_{2} \sqrt {2D_{ij} D_{ij} } } \right)}},\quad F_{2} = \tanh \left[ {\max \left( {\frac{2\sqrt k }{{\beta^{*} \omega y}},\frac{500\nu }{{y^{2} \omega }}} \right)} \right]^{2} .$$

(18)

where α₁ = 0.31, and ${\beta }^{*}=0.09$ [25]. Each constant $\varphi$ (${\sigma }_{k}$, ${\sigma }_{\omega }$, $\gamma$, $\beta$) is given by using the blending function F₁, and corresponding constant ${\varphi }_{1}$ and ${\varphi }_{2}$

$$\phi = F_{1} \phi_{1} \left( {1 - F_{1} } \right)\phi_{2} ,$$

(19)

where ${\sigma }_{k1}=0.85$, ${\sigma }_{k2}=1$, ${\sigma }_{\omega 1}=0.5$, ${\sigma }_{\omega 2}=0.856$, ${\gamma }_{1}=5/9$, ${\gamma }_{2}=0.44$, β₁ = 0.075, and ${\beta }_{2}=0.0828$ [25]. More precise descriptions about SST $k-\omega$ turbulence model should be referred to [25].