Skip to main content

Advertisement

Springer Nature Link
Log in

Estimating high-order brain functional networks by correlation-preserving embedding

  • Original Article
  • Published:
Medical & Biological Engineering & Computing Aims and scope Submit manuscript

Abstract

Brain functional network (FN) has emerged as a potential tool for identifying mental and neurological diseases. Traditional FN estimation methods such as Pearson’s correlation (PC) and sparse representation (SR), despite their popularity, can only model low-order relationships between brain regions (i.e., nodes of FN), thus failing to capture more complex interaction in the brain. Recently, researchers proposed to estimate high-order FN (HoFN) and successfully used them in the early diagnosis of neurological diseases. In practice, however, such HoFN is constructed by directly considering the columns (or rows) of the adjacency matrix of low-order FN (LoFN) as node feature vectors that may contain some redundant or noisy information. In addition, it is not really reflected whether the original low-order relationship is maintained during the construction of the HoFN. To address these problems, we propose correlation-preserving embedding (COPE) to re-code the LoFN prior to constructing HoFN. Specifically, we first use SR to construct traditional LoFN. Then, we embed the LoFN via COPE to generate the new node representation for removing the potentially redundant/noisy information in original node feature vectors and simultaneously maintaining the low-order relationship between brain regions. Finally, the expected HoFN is estimated by SR based on the new node representation. To verify the effectiveness of the proposed scheme, we conduct experiments on 137 subjects from the public Alzheimer’s Disease Neuroimaging Initiative (ADNI) database to identify subjects with mild cognitive impairment (MCI) from normal controls. Experimental results show that the proposed scheme can achieve better performance than the baseline method.

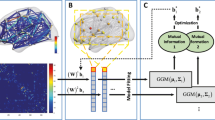
Graphical abstract

Brain functional network (FN) has emerged as a potential tool for identifying mental and neurological diseases. Traditional FN estimation methods such as Pearson’s correlation (PC) and sparse representation (SR), despite their popularity, can only model low-order relationships between brain regions (i.e., nodes of FN), thus failing to capture more complex interaction in the brain. Recently, researchers proposed to estimate high-order FN (HoFN) and successfully used them in the early diagnosis of neurological diseases. In practice, however, such HoFN is constructed by directly considering the columns (or rows) of the adjacency matrix of low-order FN (LoFN) as node feature vectors that may contain some redundant or noisy information. In addition, it is not really reflected whether the original low-order relationship is maintained during the construction of the HoFN. To address these problems, we propose correlation-preserving embedding (COPE) to re-code the LoFN prior to constructing HoFN. Specifically, we first use SR to construct traditional LoFN. Then, we embed the LoFN via COPE to generate the new node representation for removing the potentially redundant/noisy information in original node feature vectors and simultaneously maintaining the low-order relationship between brain regions. Finally, the expected HoFN is estimated by SR based on the new node representation. To verify the effectiveness of the proposed scheme, we conduct experiments on 137 subjects from the public Alzheimer’s Disease Neuroimaging Initiative (ADNI) database to identify subjects with mild cognitive impairment (MCI) from normal controls. Experimental results show that the proposed scheme can achieve better performance than the baseline method.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8

Similar content being viewed by others

Notes

  1. http://adni.loni.usc.edu/

  2. http://www.fil.ion.ucl.ac.uk/spm/

References

  1. Liu Y et al (2008) Regional homogeneity, functional connectivity and imaging markers of Alzheimer’s disease: a review of resting-state fMRI studies. Neuropsychologia 46(6):1648–1656

    Article  PubMed  Google Scholar 

  2. Azeez AK, Biswal BB (2017) A review of resting-state analysis methods. Neuroimaging Clin 27(4):581–592

    Article  Google Scholar 

  3. Geschwind DH, Levitt P (2007) Autism spectrum disorders: developmental disconnection syndromes. Curr Opin Neurobiol 17(1):103–111

    Article  CAS  PubMed  Google Scholar 

  4. Simonoff E, Pickles A, Charman T, Chandler S, Loucas T, Baird G (2008) Psychiatric disorders in children with autism spectrum disorders: prevalence, comorbidity, and associated factors in a population-derived sample. J Am Acad Child Adolesc Psychiatry 47(8):921–929

    Article  PubMed  Google Scholar 

  5. Greicius MD et al (2007) Resting-state functional connectivity in major depression: abnormally increased contributions from subgenual cingulate cortex and thalamus. Biol Psychiat 62(5):429–437

    Article  PubMed  Google Scholar 

  6. Cullen KR et al (2014) Abnormal amygdala resting-state functional connectivity in adolescent depression. JAMA Psychiat 71(10):1138–1147

    Article  Google Scholar 

  7. Wang L et al (2006) Changes in hippocampal connectivity in the early stages of Alzheimer’s disease: evidence from resting state fMRI. Neuroimage 31(2):496–504

    Article  PubMed  Google Scholar 

  8. Rombouts SA, Barkhof F, Goekoop R, Stam CJ, Scheltens P (2005) Altered resting state networks in mild cognitive impairment and mild Alzheimer’s disease: an fMRI study. Hum Brain Mapp 26(4):231–239

    Article  PubMed  PubMed Central  Google Scholar 

  9. Reijneveld JC, Ponten SC, Berendse HW, Stam CJ (2007) The application of graph theoretical analysis to complex networks in the brain. Clin Neurophysiol 118(11):2317–2331

    Article  PubMed  Google Scholar 

  10. Wang J, Zuo X, He Y (2010) Graph-based network analysis of resting-state functional MRI. Front Syst Neurosci 4:16

    PubMed  PubMed Central  Google Scholar 

  11. Pervaiz U, Vidaurre D, Woolrich MW, Smith SM (2020) Optimising network modelling methods for fMRI. Neuroimage 211:116604

    Article  PubMed  Google Scholar 

  12. Qiao L, Zhang H, Kim M, Teng S, Zhang L, Shen D (2016) Estimating functional brain networks by incorporating a modularity prior. Neuroimage 141:399–407

    Article  PubMed  Google Scholar 

  13. Friston KJ, Harrison L, Penny W (2003) Dynamic causal modelling. Neuroimage 19(4):1273–1302

    Article  CAS  PubMed  Google Scholar 

  14. Smith SM et al (2013) Functional connectomics from resting-state fMRI. Trends Cogn Sci 17(12):666–682

    Article  PubMed  PubMed Central  Google Scholar 

  15. Schwarz AJ, McGonigle J (2011) Negative edges and soft thresholding in complex network analysis of resting state functional connectivity data. Neuroimage 55(3):1132–1146

    Article  PubMed  Google Scholar 

  16. van den Heuvel MP, de Lange SC, Zalesky A, Seguin C, Yeo BT, Schmidt R (2017) Proportional thresholding in resting-state fMRI functional connectivity networks and consequences for patient-control connectome studies: Issues and recommendations. Neuroimage 152:437–449

    Article  PubMed  Google Scholar 

  17. Huang S et al (2010) Learning brain connectivity of Alzheimer’s disease by sparse inverse covariance estimation. Neuroimage 50(3):935–949

    Article  PubMed  Google Scholar 

  18. Tan Z, Yang P, Nehorai A (2013) Joint-sparse recovery in compressed sensing with dictionary mismatch. 2013 5th IEEE International Workshop on Computational Advances in Multi-Sensor Adaptive Processing (CAMSAP) 248–251. https://doi.org/10.1109/CAMSAP.2013.6714054

  19. Plis SM et al (2014) High-order interactions observed in multi-task intrinsic networks are dominant indicators of aberrant brain function in schizophrenia. Neuroimage 102:35–48

    Article  PubMed  Google Scholar 

  20. Macke JH, Opper M, Bethge M (2011) Common input explains higher-order correlations and entropy in a simple model of neural population activity. Phys Rev Lett 106(20):208102

    Article  PubMed  CAS  Google Scholar 

  21. Guo H, Liu L, Chen J, Xu Y, Jie X (2017) Alzheimer classification using a minimum spanning tree of high-order functional network on fMRI dataset. Front Neurosci 11:639

    Article  PubMed  PubMed Central  Google Scholar 

  22. Zhou Y, Qiao L, Li W, Zhang L, Shen D (2018) Simultaneous estimation of low-and high-order functional connectivity for identifying mild cognitive impairment. Front Neuroinform 12:3

    Article  PubMed  PubMed Central  Google Scholar 

  23. Chen X, Zhang H, Lee S-W, Shen D (2017) Hierarchical high-order functional connectivity networks and selective feature fusion for MCI classification. Neuroinformatics 15(3):271–284

    Article  PubMed  PubMed Central  Google Scholar 

  24. Zhao F, Zhang H, Rekik I, An Z, Shen D (2018) Diagnosis of autism spectrum disorders using multi-level high-order functional networks derived from resting-state functional mri. Front Hum Neurosci 12:184

    Article  PubMed  PubMed Central  Google Scholar 

  25. Chen X et al (2016) High-order resting-state functional connectivity network for MCI classification. Hum Brain Mapp 37(9):3282–3296

    Article  PubMed  PubMed Central  Google Scholar 

  26. Zhang H et al (2016) Topographical information-based high-order functional connectivity and its application in abnormality detection for mild cognitive impairment. J Alzheimer’s Dis 54(3):1095–1112

    Article  CAS  Google Scholar 

  27. Jia X, Zhang H, Adeli E, Shen D (2017) Consciousness level and recovery outcome prediction using high-order brain functional connectivity network. International Workshop on Connectomics in Neuroimaging 17–24. First online: 02 Sept 2017

  28. Guo T, Zhang Y, Xue Y, Qiao L, Shen D (2021) Brain function network: higher order vs. more discrimination. Front Neurosci 1033. https://doi.org/10.3389/fnins.2021.696639

  29. Zhou Y, Zhang L, Teng S, Qiao L, Shen D (2018) Improving sparsity and modularity of high-order functional connectivity networks for MCI and ASD identification. Front Neurosci 12:959

    Article  PubMed  PubMed Central  Google Scholar 

  30. Sun L, Xue Y, Zhang Y, Qiao L, Zhang L, Liu M (2021) Estimating sparse functional connectivity networks via hyperparameter-free learning model. Artif Intell Med 111:102004

    Article  PubMed  Google Scholar 

  31. Tzourio-Mazoyer N et al (2002) Automated anatomical labeling of activations in SPM using a macroscopic anatomical parcellation of the MNI MRI single-subject brain. Neuroimage 15(1):273–289

    Article  CAS  PubMed  Google Scholar 

  32. Li W, Wang Z, Zhang L, Qiao L, Shen D (2017) Remodeling Pearson’s correlation for functional brain network estimation and autism spectrum disorder identification. Front Neuroinform 11:55

    Article  PubMed  PubMed Central  Google Scholar 

  33. Chang C-C, Lin C-J (2011) LIBSVM: a library for support vector machines. ACM Trans Intell Syst Technol (TIST) 2(3):1–27

    Article  Google Scholar 

  34. Dadi K et al (2019) Benchmarking functional connectome-based predictive models for resting-state fMRI. Neuroimage 192:115–134

    Article  PubMed  Google Scholar 

  35. Guyon I, Elisseeff A (2003) An introduction to variable and feature selection. J Mach Learn Res 3(Mar):1157–1182

    Google Scholar 

  36. Gómez S, Jensen P, Arenas A (2009) Analysis of community structure in networks of correlated data. Phys Rev E 80(1):016114

    Article  CAS  Google Scholar 

  37. Rubinov M, Sporns O (2011) Weight-conserving characterization of complex functional brain networks. Neuroimage 56(4):2068–2079

    Article  PubMed  Google Scholar 

  38. Jiang X, Zhang L, Qiao L, Shen D (2019) Estimating functional connectivity networks via low-rank tensor approximation with applications to MCI identification. IEEE Trans Biomed Eng 67(7):1912–1920

    PubMed  Google Scholar 

  39. Xue Y, Zhang L, Qiao L, Shen D (2020) Estimating sparse functional brain networks with spatial constraints for MCI identification. PLoS ONE 15(7):e0235039

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  40. Greicius M (2008) Resting-state functional connectivity in neuropsychiatric disorders. Curr Opin Neurol 21(4):424–430

    Article  PubMed  Google Scholar 

  41. Albert MS et al (2011) The diagnosis of mild cognitive impairment due to Alzheimer’s disease: recommendations from the National Institute on Aging-Alzheimer’s Association workgroups on diagnostic guidelines for Alzheimer’s disease. Alzheimer’s Dement 7(3):270–279

    Article  Google Scholar 

  42. Granger CW (1969) Investigating causal relations by econometric models and cross-spectral methods. Econometrica: J Econ Soc 37:424–438

    Article  Google Scholar 

  43. Mclntosh A, Gonzalez-Lima F (1994) Structural equation modeling and its application to network analysis in functional brain imaging. Hum Brain Mapp 2(1–2):2–22

    Article  Google Scholar 

  44. Ramsey JD, Hanson SJ, Hanson C, Halchenko YO, Poldrack RA, Glymour C (2010) Six problems for causal inference from fMRI. Neuroimage 49(2):1545–1558

    Article  CAS  PubMed  Google Scholar 

  45. Smith SM et al (2011) Network modelling methods for FMRI. Neuroimage 54(2):875–891

    Article  PubMed  Google Scholar 

  46. Theiler J, Eubank S, Longtin A, Galdrikian B, Farmer JD (1992) Testing for nonlinearity in time series: the method of surrogate data. Physica D: Nonlinear Phenom 58(1–4):77–94

    Article  Google Scholar 

  47. Steuer R, Kurths J, Daub CO, Weise J, Selbig J (2002) The mutual information: detecting and evaluating dependencies between variables. Bioinformatics 18(suppl_2):S231–S240

    Article  PubMed  Google Scholar 

  48. Hamilton WL (2020) Graph representation learning. Synth Lect Artif Intell Mach Learn 14(3):1–159

    Google Scholar 

Download references

Funding

This work was partly supported by the National Natural Science Foundation of China (Nos. 61976110, 62176112, 11931008), the Natural Science Foundation of Shandong Province (No. ZR202102270451), and the Open Project of Liaocheng University Animal Husbandry Discipline (No. 319312101–01).

Author information

Authors and Affiliations

  1. School of Mathematics Science, Liaocheng University, Liaocheng, 252000, China

    Hui Su, Limei Zhang & Lishan Qiao

  2. Department of Radiology and BRIC, University of North Carolina at Chapel Hill, Chapel Hill, NC, 27599, USA

    Mingxia Liu

Authors
  1. Hui Su
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Limei Zhang
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Lishan Qiao
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. Mingxia Liu
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding authors

Correspondence to Lishan Qiao or Mingxia Liu.

Additional information

Publisher's note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Su, H., Zhang, L., Qiao, L. et al. Estimating high-order brain functional networks by correlation-preserving embedding. Med Biol Eng Comput 60, 2813–2823 (2022). https://doi.org/10.1007/s11517-022-02628-7

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11517-022-02628-7

Keywords