Pharmacokinetic/pharmacodynamic model of a methionine starvation based anti-cancer drug

Abstract

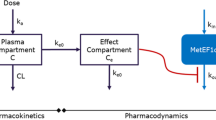
A new therapeutic approach against cancer is developed by the firm Erytech. This approach is based on starved cancer cells of an amino acid essential to their growth (the L-methionine). The depletion of plasma methionine level can be induced by an enzyme, the methionine-γ-lyase. The new therapeutic formulation is a suspension of erythrocytes encapsulating the activated enzyme. Our work reproduces a preclinical trial of a new anti-cancer drug with a mathematical model and numerical simulations in order to replace animal experiments and to have a deeper insight on the underlying processes. With a combination of a pharmacokinetic/pharmacodynamic model for the enzyme, substrate, and co-factor with a hybrid model for tumor, we develop a “global model” that can be calibrated to simulate different human cancer cell lines. The hybrid model includes a system of ordinary differential equations for the intracellular concentrations, partial differential equations for the concentrations of nutrients and drugs in the extracellular matrix, and individual based model for cancer cells. This model describes cell motion, division, differentiation, and death determined by the intracellular concentrations. The models are developed on the basis of experiments in mice carried out by Erytech. Parameters of the pharmacokinetics model were determined by fitting a part of experimental data on the concentration of methionine in blood. Remaining experimental protocols effectuated by Erytech were used to validate the model. The validated PK model allowed the investigation of pharmacodynamics of cell populations. Numerical simulations with the global model show cell synchronization and proliferation arrest due to treatment similar to the available experiments. Thus, computer modeling confirms a possible effect of treatment based on the decrease of methionine concentration. The main goal of the study is the development of an integrated pharmacokinetic/pharmacodynamic model for encapsulated methioninase and of a mathematical model of tumor growth/regression in order to determine the kinetics of L-methionine depletion after co-administration of Erymet product and Pyridoxine.

Appendices

Appendix: A

1.1 A.1 Glossary

1.1.1 A.1.1 Abbreviations

Met :

L-methionine

MGL :

methionine-γ-lyase

PN :

Pyridoxine

PLP :

Pyridoxal phosphate

CFSE :

Carboxyfluorescein diacetate succinimidyl ester

Erymet :

Suspension of erythrocytes encapsulating MGL

IG :

Intragastric

IV :

Intravenous

RBC :

Red Blood Cell

1.1.2 A.1.2 Symbols and Units

Concentration of methionine and PLP are expressed in μ M (μ mol.l^− 1). Their doses are expressed in μ mol. The quantity of enzyme is expressed with its activity. The equations for MGL are not formulated in term of concentration because of the way used to measure the amount of enzyme. Amount of enzyme are expressed in units (Symbol U or UI). A unit of enzyme is the amount of enzyme that will catalyze the formation of 1 μ mol of product per minute under specifically defined conditions. The specific activity is the amount of enzyme activity per milligram of protein. For a given pure enzyme under a defined set of conditions, the specific activity is a constant [8]. For MGL, specific activity is 16.5 UI.mg^− 1 unless otherwise specified in the text.

1.2 A.2 Signification of variables used in mathematical expression

Table 1

1.3 A.3 Parameters for mice model

Table 1 Parameters of the system of Eq. 2 estimated by Monolix

1.4 A.4 Fixed values for mice model

Table 2 Fixed values of the system of Eq. 2

1.5 A.5 Identifiability of the models

We developed a biological model of the action of an enzyme (MGL) and its co-factor (PN) on the concentration of amino acid (MET) by comparison with preclinical data. We used Monolix, a software witch estimates the parameters of the model. This software is based on the maximum likelihood estimator of the population parameters, using the Stochastic Approximation Expectation Maximization (SAEM) algorithm.

We ensured the uniqueness of parameters recovered from observed data by carried out identifiability studies of our model.

Different methods have been proposed in the literature to test identifiability of nonlinear models. For [51], identifiability is the possibility to infer parameters from the data. The structural identifiability of compartmental models has been studied has been studied over a long period [50]. In [49], Groos and al. studied a more complex problem of identifiability of linear compartment models.

In our case, we consider the identifiability of each of the submodels.

Due to the complexity of the global model (see Fig. 2), we used a software to check the identifiability of the first three submodels. This software is DAISY (Differential Algebra for Identifiability of SYstems) [48]. The results given by the software are:

• Submodels 1 and 2 are “locally identifiable”

• Submodel 3 is “globally identifiable”.

We proof the identifiability of models 4 and 5 with the following calculus. Concerning the E_max model (submodels 4 and 5), with a simplify expression of equation we consider

$$ C_{output}(t)=C_{0}\left( 1-\frac{E_{max}C_{input}(t)}{EC_{50}+C_{input}(t)}\right) $$

For a given input and two sets of parameters $\left (E^{1}_{max}, EC^{1}_{50}\right )$ and $\left (E^{2}_{max}, EC^{2}_{50}\right )$, the output should be different. Indeed, if this is not the case, then we obtain Eq. A1 which cannot hold for any non-constant function C_input(t). This contradiction proves the identifiability.

$$ \begin{array}{@{}rcl@{}} C_{input}(t)\left( E^{1}_{max}-E^{2}_{max}\right)& = &E^{2}_{max}EC^{1}_{50}- E^{1}_{max}EC^{2}_{50} \end{array} $$

(A1)

1.6 A.6 Modeling Met dietary intake (PE-TEDAC-MGL-012)

Protocol 12 provides plasma Met concentration with and without MGL administration, concentration of intraerythrocytic PLP and the activity of MGL at dates 15, 30, 45, 90, 180 and 1440 min for mice receiving an intravenous administration of MGL. PN is administered 5 days (administration date denoted: Day 0) after the injection of MGL. In what follows, time is expressed in minutes. The duration of protocol 12 is a single day (1440 min).

Fig. 11

Discursive scheme of L-methionine

Fig. 12

Daily variation of plasma Met

It was therefore possible to model the ordinary plasma level of methionine in mice (due to dietary intakes) with the data from the control population. Mice eat during night and stop their dietary intake during the day. We assume ten daily meals, even if mice have a continuous feeding.

Taking into account the composition of the food used for mice (SAFE A04), the daily intake of methionine varies between 8.4 and 16.8 mg per day per mouse. We assume a constant intake of 60 μ mol (10 mg per day per mouse) considering a molar mass of methionine equal to 149.21g.mol^− 1. $q_{MET_{1}}$, $q_{MET_{2}}$ and $q_{MET_{3}}$ (system of Eq. A2) are respectively the amount of methionine in the absorption, central and peripheral compartments. diet is the dietary intake of methionine.

$$ \begin{array}{@{}rcl@{}} \frac{d q_{MET_{1}}}{dt} &=& diet - k_{12}^{MET} q_{MET_{1}}, \text{ with }q_{MET_{1}}(0)=F.D_{i} \text{ and }i \in N\\ \frac{d q_{MET_{2}}}{dt} &=& k_{12}^{MET} q_{MET_{1}}- k^{MET}_{20}q_{MET_{2}} + k_{32}^{MET} q_{MET_{3}}\\&&- k^{MET}_{23}q_{MET_{2}}\text{, with }q_{MET_{2}(0)}=MET_{20} \\ \frac{d q_{MET_{3}}}{dt} &=& -k_{32}^{MET} q_{MET_{3}}+ k^{MET}_{23} q_{MET_{2}}, \text{ with }q_{MET_{2}(0)}=MET_{20} \\ C_{MET_{2}}&=&\frac{q_{MET_{2}}}{V_{MET}} \end{array} $$

(A2)

1.6.1 Internal validation

1.7 A.7 Modeling of the intraerythrocytic PLP (PE-TEDAC-MGL-012)

Protocol PE-TEDAC-MGL-012 studied the pharmacokinetics of PLP (vitamin B₆ oral uptake at day 0) following the MGL administration (at day -5). This protocol provides intraerythrocytic PLP concentrations at times 15, 30, 45, 90, 180 and 1440 min after an intragastric administration of PN for mice receiving PN, that is metabolized in PLP.

$$ \begin{array}{@{}rcl@{}} \frac{d q_{PN}}{dt} & =& ad-\frac{V_{max}}{\left( k_m+\frac{q_{PN}}{V_{PN}}\right)}\frac{q_{PN}}{V_{PN}}-k_{10}^{PN}q_{PN},\ \ q_{PN}(0)=PN_0 \\ \frac{d q_{PLP}}{dt} &=& \frac{V_{max}}{\left( k_m+\frac{q_{PN}}{V_{PN}}\right)}\frac{q_{PN}}{V_{PN}} - k_{20}^{PLP}q_{PLP},\ \ q_{PLP}(0)=0 \\ C_{PN}(t) &=& \frac{q_{PN}(t)}{V_{PN}} \\ C_{PLP}(t) &= &\frac{q_{PLP(t)}}{V_{PLP}} \end{array} $$

(A3)

Fig. 13

Simulation with the model: Erymet intraerythrocytic PLP data modeled concentration in three mice. Y-axis: intraerythrocytic concentration of PLP (μM), x-axis: time (min)

1.7.1 Internal validation

1.8 A.8 Modeling MGL kinetic (PE-TEDAC-MGL-013)

PLP is the co-factor of the enzyme (MGL) and is encapsulated with MGL in red blood cells to activate this enzyme. PLP progressively disappears, explaining an increasing inactive part of MGL.

Fig. 14

Discursive scheme of MGL activity. Left: Total MGL. Right: Relationship between active and not active MGL. The first three in Eq. A4 describe this relationship

Fig. 15

Erymet data: control population of protocol 13 (mean value). Y-axis: (a) total activity of MGL. (b) spontaneously active MGL. (c) non spontaneously active MGL. x-axis: time (days). Green curve: values obtained with the model. Blue crosses: observed values

Fig. 16

Met as a function of encapsulated MGL in mice (experimental values from Erytech protocol, PE-TEDAC-MGL-014). Mice receive PN two time per a day after Erymet administration. Curve for mean values

We first modeled the activity of MGL without administration of PN. We have denoted by “total activity”, the MGL activity measured with PLP against a range carried in biological matrix, “spontaneously active MGL” is the loaded in co-factor MGL and “non spontaneously active MGL” is the difference between the total and spontaneously active MGL. We used the system of Eq. A4 to describe this part of protocol 13 and the system (A2) to describe the methionine depletion after an IV of Erymet (first with PLP= 0).

$$ \begin{array}{@{}rcl@{}} \frac{dMGL_{a}}{dt} &=&-k^{MGL}_{a,i}MGL_{a} + k^{MGL}_{i,a}MGL_{i} \\&&+ p.k^{MGL}_{p,t}MGL_{p}-k^{MGL}_{t,p}MGL_{a} \\&&-k^{MGL}_{e} MGL_{a}, \text{with } MGL_{a}(0)=D \\ \frac{dMGL_{p}}{dt}&=& -k^{MGL}_{p,t}MGL_{p} + k^{MGL}_{t,p}MGL_{a} \\&&+ k^{MGL}_{t,p}MGL_{i}, \text{ with } MGL_{p}(0)=0 \\ \frac{dMGL_{i}}{dt}&=& k^{MGL}_{a,i}MGL_{a} -k^{MGL}_{i,a}MGL_{i}\\&&+(1-p).k^{MGL}_{p,t}MGL_{p}-k^{MGL}_{t,p}MGL_{i} \\&&-k^{MGL}_{e} MGL_{i}, \text{with } MGL_{i}(0)=0 \\ C_{MGL_{a}}&=&\frac{MGL_{a}}{V} \\ C_{MGL_{i}}&=&\frac{MGL_{i}}{V} \\ C_{MGL_{tot}} &=&C_{MGL_{a}}+C_{MGL_{i}} \end{array} $$

(A4)

1.8.1 Internal validation

1.8.2 A.8.1 Modeling pharmacodynamic of MGL

Choice of the model

At the time of its injection, the enzyme is in its active form (PLP is encapsulated with the enzyme). The global activity decreases rapidly and the remaining enzyme becomes more or less inactive depending on the amount of available PLP. We can observe the absence of hysteresis in experimental data and this could suggest a direct response model (see Fig. 16). Met as a function of encapsulated MGL in mice (experimental values from Erytech protocol, PE-TEDACMGL- 014). Mice receive PN two time per a day after Erymet administration. Consequently, a direct response model (Hill model) was chosen.

Modeling

The control population of protocol PE-TEDAC-MGL-013 provides activity of total MGL, activity of the activated MGL (by the initial encapsulation of PLP) and the part of the non activated MGL as a functions of time. The percentage of activated MGL decreases while the percentage of non activated MGL increases. Obviously, the activity of the total MGL decreases with time. We compared the activity of MGL with and without IG administrations of PN. We choose a direct model for the effect of PLP on MGL activity. To evaluate the importance of PN supplementation, we added Eq. A5 to the system (A4).

$$ \begin{array}{@{}rcl@{}} C^{obs}_{MGL}&=&C_{MGL_{a}}^{PLP}=C_{MGL_{a}}\left( 1+\frac{E_{{max}^{PLP}}^{a} C_{PLP}}{EC_{50}^{PLP}+C_{PLP}}\right) \\ C_{MGL_{a}}^{PLP}&=&C_{MGL_{a}}\left( 1+\frac{E_{{max}^{PLP}}^{a} C_{PLP}}{EC_{50}^{PLP}+C_{PLP}}\right) \\ C_{MGL_{i}}^{PLP} &=&C_{MGL_{i}}\left( 1-\frac{E_{{max}^{PLP}}^{i} C_{PLP}}{EC_{50}^{PLP}+C_{PLP}}\right) \\ C_{MGL_{tot}}^{PLP}&=&C_{MGL_{a}}^{PLP}+C_{MGL_{i}}^{PLP} \end{array} $$

(A5)

1.8.3 Internal validation

Table 3 Parameters of the system of Eq. A5 estimated by Monolix

Fig. 17

Erymet data: supplemented by PN population of protocol 13 (mean value). Y-axis: (a) total activity of MGL. (b) spontaneously active MGL. (c) non spontaneously active MGL. (d) Met concentration (μM). x-axis: time (days). Green curve: values obtained with the model. Blue crosses: observed values

1.9 A.9 Modeling Met depletion (PE-TEDAC-MGL-012, 013)

The amount of the substrate (Met) decreases in the presence of the enzyme (MGL). Figure 18 shows a typical situation for which a direct response model is widely used. Consequently, we chose a direct response model for the effect of MGL on plasma Met.

After an administration of MGL and a supplementation with PN, the observed Met is described by

$$ \begin{array}{@{}rcl@{}} C_{MET_{obs}}=C_{MET_{2}}\left( 1-\frac{E_{max}^{MGL}C^{obs}_{MGL}}{EC_{50}^{MGL}+C^{obs}_{MGL}}\right) \end{array} $$

(A6)

1.9.1 Internal validation

Development of the three submodels (modeling Eytech’s data from Protocols PE-TEDA-MGL-012, 13 and 14) can be seen in more details in Appendix A.7 for modeling of the intraerythrocytic PLP (PETEDAC-MGL-012), in Appendix A8 for enzime activity and in Appendix A.6 for modeling Met dietary intake (PE-TEDAC-MGL-012).

Fig. 18

Erytech data, protocol PE-TEDAC-MGL-012. x-axis: time (min). y-axis: plasma level of Met (μ M). Blue curve, control population. Red curve, population receiving MGL

Table 4 Parameters of the systems of Eq. A6 estimated by Monolix

Appendix: B. E _max model

The effect E is a measurable property whose nature depends on the tested drug. E may be the patient’s blood pressure drop or blood cholesterol levels, etc...

1.1 B.1 Action of the enzyme on the amino acid

In our case, the way to observe the effect of the drug is the measurement of blood methionine concentration and the effect E is its depletion. The differences between notation, due to the approaches differences, are summarized in the Table 5.

Fig. 19

(a) Modeled plasma L-methionine concentration (control population in protocol 13: mice not receiving injection of MGL). (b) Modeled plasma L-methionine concentration in mice receiving injection of MGL in protocol 13. (c) Modeled plasma L-methionine concentration in mice receiving injection of MGL in protocol 12. (d) Modeled plasma L-methionine concentration in mice receiving injection of MGL in protocol 14. Y-axis: concentration of Met (μM), x-axis: time (min)

Table 5 Notations meaning

The classical E_max model of PK/PD modeling is established in the following calculus:

$$ \begin{array}{@{}rcl@{}} &&[D]+[R] \overset{k_{1}} \leftrightarrows \underset{k_{2}} [D\sim R ]\\ &&\frac{[D\sim R ]}{dt} = k_{1} [D][R] - k_{2} [D\sim R] \end{array} $$

Let y the ratio of methionine receptors occupied by methionine-γ-lyase, i.e., the ratio of methionine which have reacted to form $[D\sim R]$.In equilibrium conditions, we may define [R_t], as the entire concentration of R As a consequence, $y = \frac {[D\sim R]}{R_{t}} \text {, with } [R_{t}] = [R] + [D\sim R ]$

$$ [D\sim R] = [R_{t}] - [R] \text{, so }1-y= \frac{[R]}{[R_{t}]} $$

(B1)

We assume that the dissociation and association rates are equal when equilibrium state is reached,with dissociation rate = k₂y and association rate = k₁[D](1 − y), so k₁[D](1 − y) = k₂y

$$ \begin{array}{@{}rcl@{}} y &=& \frac{[D]}{[D] + \frac{k_{2}}{k_{1}}}\\ y &=& \frac{[D]}{[D] + k_{G}}\\ \end{array} $$

$\text {On the other hand for an inhibition action, by definition: }y = \frac {E_{0} - E}{E_{max}}$

$$ \begin{array}{@{}rcl@{}} E = E_{0} - E_{max} \frac{[D]}{[D] + k_{D}} \end{array} $$

(B2)

with k₁ = kinetic constant of association, k₂ = kinetic constant of dissociation, k_A = association constant = $\frac {k_{1}}{k_{2}}$, k_D = dissociation constant = $\frac {k_{2}}{k_{1}}$.

Let k_D = EC₅₀. In what follows $\frac {E_{max}}{E_{0}}$ is denoted E_max and is an unit-less quantity.

We obtained $E = E_{0}\left (1 - E_{max} \frac {[D]}{[D] + EC_{50}}\right )$, i.e., $C_{MET_{obs}} = C_{MET_{2}}\left (1-\frac {E_{max}^{MGL}{MGL_{obs}}}{EC_{50}^{MGL}+C_{MGL_{obs}}}\right )$ with the notation of the whole model.

We can notice without drug administration ($C_{MGL_{a}} = 0$), $C_{MET_{obs}} = C_{MET_{2}}$.

1.2 B.2 Action of PN administration on encapsulated methionine-γ-lyase

PN becomes PLP, witch is the co-factor of the enzyme consequently the effect of the drug (PLP) is the increase in activity of encapsulated methionine-γ-lyase, then $E = C_{MGL_{a}}^{PLP}$ and the baseline effect prior to drug administration $E_{0} = C_{MGL_{a}}$, i.e., E₀ is the activity without PLP administration.

MGL_a and MGL_i are active and inactive encapsulated methionine-γ-lyase amount in the central compartment (the administered red cells loaded with the enzyme). MGL_p is the amount of enzyme in the peripheral compartment.

In order to simplify the reading of Eq. B3, $C_{MGL_{a}}$ is denoted [G] and C_PLP is denoted [P].

$$ \begin{array}{@{}rcl@{}} & &[P]+[G] \overset{k_{1}} \leftrightarrows \underset{k_{2}} [P\sim G ] \\ & &\frac{[P\sim G ]}{dt} = k_{1} [P][G] - k_{2} [P\sim G] \\ \end{array} $$

equilibrium equation, $\frac {[P\sim G ]}{dt} =0 \text {, } k_{1} [P][G] = k_{2} [P\sim G ]$Let y, the number of agonist occupied receptors.We assume that the dissociation and association rates are equal, with dissociationrate = k₂y,association rate = k₁[P](1 − y),so k₁[P](1 − y) = k₂y

$$ \begin{array}{@{}rcl@{}} y & =& \frac{[P]}{[P] + \frac{k_{2}}{k_{1}}} \\ y &=& \frac{[P]}{[P] + k_{D}} \\ {[G_{t}]} &=& [G] + [P\sim G ] \\ y &=& \frac{[P\sim G ]}{[G_{t}]} \\ y &=& \frac{E - E_{0}}{E_{max}},\text{for a potentiator action } \\ E &=& E_{0} + E_{max} \frac{[P]}{[P] + k_{D}} \end{array} $$

(B3)

We obtained $E = E_{0}\left (1 + E_{max} \frac {[P]}{[P] + EC_{50}}\right )$ i.e., $C_{MGL_{a}}^{PLP} = C_{MGL_{a}}\left (1+\frac {E_{{max}^{PLP}}^{a} C_{PLP}}{EC_{50}^{PLP}+C_{PLP}}\right )$ with the notation of the whole model.

Appendix: C Computational aspects and parameters assessment

The global model PK/PD has been implemented with MLXTRAN code (the language for describing models and treatment design of the Monolix software, a software for nonlinear mixed effects modeling) to assess parameters, their values are given in Table 1 and some parameters are assessed by nonlinear multiple regression method implemented in Scilab. The output variables were total MGL, active MGL, non active MGL, PLP and Met. For each variable, we used a constant error. The standard errors were obtained by linearization, with conditional modes for individual parameters and were obtained by linearization for Log-likelihood.

Simulations of PK/PD model have been made by writing code with Scilab, the system of ordinary differential equations has been solved by the ordinary differential equation solver “ode”, specific code has been written to solve the system taken into account various frequency of administrations.

The tumor model is implemented in C⁺⁺ with the operating system Ubuntu and a graphical library wxWidget [39] included in specific software developed [40, 41]. Cell divisions are model as follows: during cell cycle, cell radius grows linearly. It becomes twice the initial radius at the end of the cycle. Then, each mother cell is replaced by two daughter cells. Geometrically, two circles with the initial radius are located inside the circle with a twice larger radius. The direction of cell division, that is the direction of the line connecting the centers of daughter cells is random [39]. On a computer view, a cell is a set of parameters. In order not to have a predetermine cell behavior, these values can vary with time and cells location. Each cell has its own initial and critical values and coefficients of equations considered in the model. Their fate depend on the computation results done during their whole life. To increase legibility of this representation, cells can not overlap. It is therefore necessary to consider their positions and displacements. A more complete approach of cells motion in hybrid models can be found in [39, 41,42,43,44].

The equations of the model are solved with an algorithm involving the spatial discretization of a computational domain and discretization of the time of simulation, i.e., each iteration of the computation corresponds to a time step Δt. In numerical simulations, Eq. 6 is solved by a finite difference method with Thomas algorithm and an alternative direction method. Neumann (no-flux) boundary conditions are considered as the boundary of the rectangular domain (L x L) [39, 44]. Constant space and time steps are used. Equation 7 is solved by Euler method.

In Eq. 6, the consumption rate of methionine by cancer cells is calculated as follows (see [45]): A local cell concentration c is computed as total cell area inside each square of the grid. For simplicity of calculation of cell concentration we make an assumption that cell is square (see Fig. 20). If one square grid of numerical scheme is completely inside of the cell, then concentration is equal

$$c_{1} = \frac{\frac{dxdy}{4R^{2}}}{dxdy} = \frac{1}{4R^{2}}$$

Otherwise, cell concentration is

$$c_{2} =\frac{\frac{x_{m} y_{m}}{4R^{2}}}{dxdy}$$

Next, we distribute the concentration between the nodes dividing c₁ and c₂ by 4. Then we compute the values of the concentration at the nodes of the numerical grid corresponding to Eq. 6.

Fig. 20

The square grid shows the numerical mesh used to solve reaction-diffusion equations. Concentration at all grid nodes is computed and then the values at the nodes are interpolated to the cell center x = x_i of Eq. 6. Source Polina Kurbatova Thesis [45]