1 Introduction

Cardiovascular disorders (CVDs) are the most prevalent causes of worldwide mortality, constituting 32\(\%\) of all fatalities, with approximately 17.9 million individuals yearly [1]. Cerebrovascular diseases influence the dynamics of blood flow to the brain [2]. Intracranial aneurysms (IAs) are abnormal bulges of an artery, which often appear at major branch spots of the circle of Willis [3]. After reaching sufficient size, an aneurysm may rupture, when it reaches ultimate stress. The two major treatment options for IAs are craniotomy clipping and endovascular coiling [4]. Coil embolization is the leading endovascular treatment option for IAs. In coil embolization, the IA sac is implanted with coils, which are metallic implants that cause thrombotic occlusion and isolate aneurysm from the intracranial blood circulation [5, 6]. However, this treatment remains disputable because endovascular therapy has a greater risk of recurrence. To overcome these issues, several studies have been carried out to understand the risk factors for the recurrence of an aneurysm in coil embolization [7, 8].

Fig. 1
figure 1

(a) Actual geometric form of the embolization coil and (b) idealization in the form of a compliant cylindrical rod

Full size image

Embolization coils are developed by a sequence of modifications from primary to secondary to tertiary structure. The primary structure of the embolization coil is called stock wire (D1), with diameter ranging from 0.044 to 0.076 mm. The secondary structure (D2) of the embolization coil is developed by winding the stock wire around a mandrel [9], shown in Fig. 1a. Previous studies [10,11,12] have performed embolic coil simulation with an ideal aneurysm model to study the hemodynamic changes. Earlier studies [13,14,15] analyzed the stent-assisted coiling method to look at the intra-aneurysmal hemodynamic alteration. Some studies [11, 16,17,18] have focused on the virtual coil placement technique to understand the aneurysm inflow modifications. Finite Element Method (FEM) based coil insertion techniques to place the embolic coil inside the aneurysm and analyze the respective intra-aneurysmal hemodynamic modifications are available in [10, 12, 14, 15, 19, 20]. The predefined coil placement using the geometric modeling technique is utilized in a few studies [21, 22]. In our recent study [23], the packing density of the coil was assumed to be uniform and homogeneous resulting in an equivalent porous medium-based model. Although such simulations provide an approximate flow characterization and hemodynamic parameters in a weighted average sense, it lacks the details of the coil interaction with the flow into the aneurysm. This motivated us to study the interaction of coil geometry that obstructs the flow into the domain of the aneurysm. Most mentioned in the literature have assumed the embolization coil to be a continuous cylindrical structure (circular cross-section), as shown in Fig. 1b. In actual practice, the embolization coil has primary and secondary structures, as shown in Fig. 1a. All the embolization coil simulations performed till now considered only secondary diameter; these studies ignored the effect of blood flow in the gap regions of primary coil structure. In reality, such compliant cylindrical rod-like primary coil alone, cannot enable compliant filling inside the aneurysm sac.

The framing coil (first coil inserted) is intended to fill the vicinity of the aneurysm sac. A single coil could be implanted to embolize or prevent future recurrence in the case of a small-size aneurysm. The framing coil’s role as the initial barrier to aneurysm sac inflow is critical when further coils are introduced, because it may behave as a flow diverter, which will promote thrombosis. Inserting additional coils increases the coil packing density (CPD). It was observed that, at a CPD of more than 20\(\%\), its influence on hemodynamics is insignificant [22, 24]. In order to estimate the success of aneurysm embolization, it is important to consider how the framing coil orientation affects hemodynamic changes. Compared to CPD, the significance of framing coil orientation is not well known. Very few studies [21, 22] have investigated the effects of framing coil orientation on the hemodynamics of an aneurysm; these studies have assumed the coil structure to be cylindrical in shape which is not an exact representation of the actual embolic coil shape. However, to the best of authors’ knowledge, none of the numerical investigations has performed simulations using actual coil structure. Hence, the present study addresses the effects of framing coil orientation on hemodynamics by considering the actual details of the coil structure (both primary and secondary). After identifying the most appropriate framing coil loop (FCL) orientation, it is hypothesized that the aneurysm volume is filled with the embolic coil with an equivalent porous medium to facilitate the study of the hemodynamics of complete coiling. Section 2 briefly describes the approach to the problem under consideration. Coil embolization validation studies are presented in Sect. 3. Detailed simulations are performed in Sect. 4. In Sect. 5, conclusion along with limitations of the present study is discussed.

Fig. 2
figure 2

(a) Ideal framing coil inserted inside an aneurysm. (b) Typical dimensions of basilar tip aneurysm model and position of the framing coil. (c) Porous coil embolization with framing coil

Full size image

2 Solution methodology

2.1 Geometric model

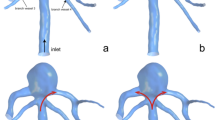
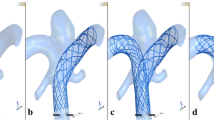
An ideal geometric model of a basilar tip aneurysm was created in SolidWorks [25]. The dimensions of an aneurysm model are shown in Fig. 2. The aspect ratio (diameter (D) to height (H)) of the aneurysm was chosen as D/H\(=\)1.1, which closely resembles clinically observed data [10]. Typical coil fill associated with such an aneurysm for patient management is modeled with the aid of specific dimensions. The primary (D1) and secondary (D2) diameters of the framing coil are 0.06 mm [9], and 0.31 mm [10] respectively. The gap distance between each primary coil turn is 0.004 mm. A typical framing coil placed near the wall of the aneurysm is shown in Fig. 2a. Resolving the mesh details closer to the coil winding, which is engulfing the aneurysm walls and covering the neck, is highly difficult and time-consuming in the numerical simulations. Since the objective of this study is to investigate the effects of FCLs position and orientation on the intra-aneurysmal hemodynamics, considering the small length of the framing coil, which covers the neck of aneurysm is sufficient. Such a study is expected to provide insights into blockage aspect of the flow through the neck of the aneurysm and into the sac region. The length of each loop is 4.86 mm, which covers only the neck portion of the aneurysm. Although in reality, the framing coil has a complex shape, the position of the framing coil is assumed to be as shown in Fig. 2b; the first loop diameter of the framing coil is 5.05 mm. Figure 2b shows the front view of a single loop framing coil. When the aneurysm is filled with an embolic coil, an equivalent porous medium model is constructed, with complete representation of the framing coil presented in Fig. 2c. Overall, nine framing coil loops are positioned near the neck of the aneurysm, as shown in Fig. 3. Different orientations of framing coils under investigation are shown in Fig. 3c, d, e, and f. Coil A is oriented along two outlets, while coil B, C, and D orientations are varied by 30\(^0\), 60\(^0\), and 90\(^0\) respectively.

Fig. 3
figure 3

Aneurysm model with (a) no coil, (b) ideal coil shape and (c, d, e, and f) different orientations for the framing coil

Full size image
Table 1 Details for 3 different types of grid used in the present study
Full size table

2.2 Computational fluid dynamics (CFD) methodology

Given the above configuration and the associated coil fill, it is imperative to understand the basilar tip aneurysm model without framing coil. To analyze the effects of actual embolic coil shape instead of ideal embolic coil shape, two simulations are carried out in the same framing coil position with the ideal and actual embolic coil shape, as shown in Fig. 3b and c. To study the effects of different orientations of FCL, three distinct simulations are performed as shown in Fig. 3d, e, and f. All geometric models developed were imported to COMSOL Multiphysics [26] to perform CFD simulations. To obtain detailed fluid dynamical activity inside the aneurysm, the Navier-Stokes equations were solved in COMSOL Multiphysics by utilizing the assumptions of laminar, transient, and incompressible flow. Although blood is a multi-component fluid, it is assumed as a Newtonian fluid as a first approximation [27,28,29]. The density and viscosity of blood considered are, 1060 kg/m\(^3\) and 0.00371 Pa-s [10] respectively. Wall boundary of the basilar tip aneurysm model and surfaces of FCLs were considered as rigid, and no-slip on the walls. The pulsatile velocity profile was imposed at the inlet, as shown in Fig. 5 [30]. A traction-free exit pressure was applied at both outlets [10]. The steady-state solution is obtained by performing simulations for six cardiac cycles for each case, and results from the last two cycles (5th and 6th) were found to be steady and periodic. The results from the last cardiac cycle are used for time-averaging hemodynamic parameters. The grid sensitivity study was carried out using Coil D with three structured mesh densities (coarse, medium, and fine), as shown in Table 1.

Fig. 4
figure 4

Computational mesh details for a typical coil. (a) Front view, (b) side view, and (c and d) zoomed views near the neck of the aneurysm

Full size image

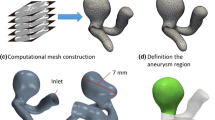
The meshed computational model is shown in Fig. 4. Figure 4a and b represent the front and side views of the meshed model. The cross-sectional view of the meshed model is shown in Fig. 4c and d to visualize the details of the mesh generated in the vicinity of the fluid and solid domains. The tetrahedral, prism, and triangular elements are used to generate the hybrid mesh of the computational domain. Three prismatic boundary layers are particularly generated to resolve the local gradients accurately. A reasonable grid size is chosen by taking care of a compromise between the computation accuracy and the simulation duration. The value of the first layer thickness is 0.05 times of local domain element height, and adequate near-wall resolution was provided. A detailed grid sensitivity was carried out by choosing the intra-aneurysmal velocity from the neck of the aneurysm (Coil D) at central axis during four distinct time levels of the last cardiac cycle (T1, T2, T3, and T4), shown in Fig. 5. It was observed from Fig. 6 that the relative error between medium and fine mesh was less than 3\(\%\) for the normalized velocities. Therefore in this study, a medium-sized mesh is found to be adequate and further used for performing all simulations.

Since the inlet boundary condition is pulsatile, the computational results are time-dependent and corresponding variations are influenced by time-periodicity. In view of this, the simulations have steady periodic variation, instead of a steady-state solution. Typical variation of velocity residual as a function of the cardiac cycle is plotted for six cycles, as shown in Fig. 7. The residual velocity error is calculated as follows:

$$\begin{aligned} \text{ Residual } \text{ error } \varepsilon (t)=\Vert u(t)-u(t-T)\Vert \end{aligned}$$
(1)

where T refers to the cardiac cycle time. It can be observed that the residual variations follow the steady periodic nature of inlet velocity.

Fig. 5
figure 5

Temporal variation of the inlet velocity profile (for a typical patient-specific case). Such pulsatile profiles would be typically obtained from a transcranial Doppler measurement

Full size image
Fig. 6
figure 6

Coil D aneurysmal inflow velocity at T1, T2, T3, and T4

Full size image
Fig. 7
figure 7

Convergence study: Steady periodic velocity residuals for few cardiac cycles

Full size image

2.3 Porous medium model (PMM) for the embolic coil

Although the objective of the present study is to identify the most appropriate framing coil orientation, it is important to study the actual aneurysm volume with the embolic coil. The coil fill volume is difficult to resolve in terms of its complete representation. Hence, an equivalent porous medium was assumed to be present with a suitable packing density. The porous medium model (PMM) utilizes homogenous and isotropic porous media simplification, which is governed by Darcy’s law, to resolve the complex geometry of embolic coils. The equivalent porosity and permeability for the deployed embolic coils are represented by adding the source term to the Navier-Stokes equation. The standard assumption of linear relation between velocity and pressure drop is assumed in each direction. The associated equations based on the permeability of the porous medium are as follows [31,32,33].

$$\begin{aligned} \rho \left( \frac{\partial \varvec{u}}{\partial t}+\nabla \cdot \left( \frac{\varvec{u} \varvec{u}}{\phi }\right) \right) =-\nabla p+\mu \nabla ^2 \varvec{u}-\frac{\mu \phi \varvec{u}}{K} \end{aligned}$$
(2)

where \(\rho \) is fluid density (\(kg/m^{3}\)), \(\varvec{u}\) is superficial velocity (m/s), t is time (s), \(\phi \) is porosity, p is pressure (\(kg/ms^{2}\)), \(\mu \) is dynamic viscosity (kg/ms), and K is permeability (\(m^{2}\)).

$$\begin{aligned} \phi= & {} 1-PD \end{aligned}$$
(3)
$$\begin{aligned} PD= & {} \frac{TCV}{ADV} \end{aligned}$$
(4)

where PD is the Packing Density, which is the ratio of Total Coil Volume (TCV) in \(mm^{3}\) to Aneurysm Dome Volume (ADV) in \(mm^{3}\) [34]. The permeability of the porous domain is calculated using the Carman-Kozeny relation.

$$\begin{aligned} K = \frac{\phi ^3}{cA^2} \;\;\; A = \frac{ISA}{ADV} \end{aligned}$$
(5)

where c is the Kozeny coefficient, the value of c is 2 for cylindrical tubes. ISA is the Internal surface area of the porous region.

Fig. 8
figure 8

Validation result of coil embolization simulation

Full size image

3 Validation of coil embolization simulation

The hemodynamics of blood flow after coil embolization is validated by performing simulations for the same case as, Babiker et al. [10]. In their work, they have validated the coil embolization simulation results with in-vitro and in-vivo experiments. CFD simulation after coil insertion is done by applying an inlet mass flow rate of 5 ml/s to the inlet of the ideal basilar tip aneurysm, and zero pressure is applied at both outlets. The basilar tip aneurysm has an inlet and outlets of 4 mm diameter each and an aspect ratio of 1.1. The volume of blood is considered as a Newtonian fluid, with viscosity and density of 0.00371 Pa-s and 1060 kg/m\(^3\), respectively. The basilar tip aneurysm wall was assumed to be rigid, and no-slip BC was given to walls. Figure 8 presents a comparison of normalized velocity along the central axis of the aneurysm from the neck, towards the inlet. A reasonable agreement may be noticed between the two. Validation of the solver for porous medium approximation is available in our previous work [23]. In that study, an idealized model aneurysm of Cha et al. [35] was utilized for solver validation of porous medium approximation. For this tube bifurcation model, flow boundary condition was imposed in the inlet, and constant pressure was applied to both outlets. The coiled aneurysm has packing density and porosity of 30\(\%\) and 0.7, respectively. The average flow rate for a single cardiac cycle before coiling was used to normalize the flow rate across the aneurysm neck plane after coiling with a porous medium. A significant comparison of the normalized volume flow rate at the aneurysm neck plane confirms the validation of flow through the porous medium model.

4 Results and discussion

4.1 Fluid flow features

The main goal of endovascular coil embolization is to significantly curtail the blood flow into intra-aneurysmal space and reduce the flow and promote thrombus formation [36]. CFD simulations enable the determination of flow velocity in the intra-aneurysmal region for various coil orientations. The velocity magnitude (VM) is plotted as a color map at XY central plane as shown in Figs. 9, 10, and 11. Figure 9 shows the overall effect of different FCL orientations on intra-aneurysmal flow. Intra-aneurysmal flow deviation from the neck of the aneurysm to outlets due to the FCLs is clearly observed in Fig. 9. Figure 9 (a, b, and c) shows the VM of the basilar tip aneurysm without the framing coil. In this case, blood is freely allowed into the space of the aneurysm without any blockage. Figure 9 (d, e, and f) shows the VM for the ideal framing coil (Coil X), which blocks the intra-aneurysmal flow.

The effect of actual practice embolic coil shape (Coil A) instead of the ideal coil shape (Coil X) on intra-aneurysmal flow velocity is shown in Fig. 9 (g, h, and i); both Coil A and Coil X were placed in the same orientation, and the only difference is the framing coil shape. There is a considerable difference between ideal coil shape and coils with actual shapes on intra-aneurysmal flow VM, which is clearly brought out through a number of parameters, as depicted in Figs. 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, and 19. Figure 9 (j, k, and l) shows the VM of Coil B, which is rotated counterclockwise by 30\(^0\) from Coil A position. Due to this, VM at the gap between each loop of framing coil is more in Coil B when compared to Coil A. Coil C effects on intra-aneurysmal flow VM are shown in Fig. 9 (m, n, and o). It was observed that, among the FCL’s, Coil A blocks inflow better compared to other Coil (B, C, and D) orientations. Coil D position allows higher inflow than other framing coil orientations, which is clearly shown in Fig. 9 (p, q, and r).

Fig. 9
figure 9

Color map for the magnitude of flow velocity at XY central plane during T1, T2, and T3

Full size image
Fig. 10
figure 10

Flow velocity below 20 mm/s at XY central plane during T1, T2, and T3

Full size image
Fig. 11
figure 11

Flow velocity below 2 mm/s at XY central plane during T1, T2, and T3

Full size image
Fig. 12
figure 12

Y-component of flow velocity above FCLs (1.85 mm above the neck plane) for all cases

Full size image
Fig. 13
figure 13

Volume flow rate into the aneurysm over the cardiac cycle

Full size image
Fig. 14
figure 14

Residual flow volume of all above 10 mm/s during peak systole (T1): (a) No coil, (b) Coil X, (c) Coil A, (d) Coil B, (e) Coil C, (f) Coil D

Full size image
Fig. 15
figure 15

Vorticity magnitude at XY central plane during T1, T2, and T3

Full size image
Fig. 16
figure 16

Intra-aneurysmal velocity magnitude during T1, T2, and T3 in aneurysm without coil (No Coil)

Full size image
Fig. 17
figure 17

Intra-aneurysmal velocity magnitude during T1

Full size image
Fig. 18
figure 18

Intra-aneurysmal velocity magnitude during T2

Full size image
Fig. 19
figure 19

Intra-aneurysmal velocity magnitude during T3

Full size image

In Figs. 10 and 11, the normalized velocity vectors are superimposed with VM, and the range of the VM is limited to 20 mm/s in Fig. 10 so that velocity magnitude changes inside the aneurysm dome could be observed from the aneurysm neck area. Also, in Figs. 10 and 11, only the aneurysm portion is shown in a zoomed view. The VM variations within the embolic coil are clearly visible in Fig. 10 (g, h, and i), which is not obvious in Fig. 10 (d, e, and f) because of the ideal coil shape. Note that the ideal coil shape has a continuous cylindrical structure (with circular cross-section) as shown in Fig. 10 (d, e, and f). By utilizing the coil shapes used in clinical practice, it is possible to analyze the VM changes within the embolic coil as it mimics the intra-aneurysmal flow better. During T1 and T2, Coil A has lower zone of VM (greater than 20 mm/s) compared to other coil orientations. During T2, intra-aneurysmal VM is higher near the aneurysm wall rather than in the central core. During T3, VM is higher at the center region of the aneurysm than near aneurysm wall region, which is clearly observable in Fig. 10. Coil D has a larger zone of VM (greater than 20 mm/s) in comparison with other coil orientations. In the central core of the aneurysm with coil, two recirculating eddies may be noticed, albeit with reduced strength. However, when coil is not present, these two eddies are confined closer to the dome region. The cardiac phase at entry of the inlet has a definite time delay before its influence is felt near the fundus and dome.

To investigate the VM changes inside the coil area, in Fig. 11 the VM range is limited to 2 mm/s, so that it is possible to analyze the effect of FCL orientations on VM changes in the vicinity of the embolic coil. However, with an ideal coil shape (Coil X), the blockage effect persists, which obstructs both inflow into the aneurysm and outflow from the sac of the aneurysm region. Coil A has a wider zone of VM (greater than 2 mm/s) than other models, during T1, T2, and T3. For Coil B, the central and end framing coils have less than 2 mm/s VM during T2. During T1, none of the framing coils has VM of greater than 2 mm/s. In the orientations of Coil C and Coil D, all the framing coil loops have a VM of less than 2 mm/s. However, it is not clear on why a particular coil orientation is able to block the flow into the aneurysm better. To this end, the intra-aneurysmal flow velocity (Y-Component) above the FCLs (1.85 mm from aneurysm neck) is shown in Fig. 12. It may be observed that coil orientation has a definite influence due to the nature of return flow into the bifurcating outlets. Although Coil X is able to block better, it is not the standard practice coil shape. Among the FCL orientations, Coil A is found to have superior blockage characteristics. A wider zone of high velocity is observable in Coil B, Coil C and Coil D orientations, signifying not so efficacious nature of the FCL orientation. Furthermore, volume flux through the neck plane (1.85 mm above neck) of the aneurysm is observed.

The volume flow rate (VFR) into the aneurysm (1.85 mm above neck plane) during cardiac cycle is plotted in Fig. 13 for different orientations of FCL. Although net volume flow rate through the aneurysm is zero, due to mass conservation, the rate of volume flow will enable an understanding of the momentum being impeded by the framing coil orientations. Coil X allows the least VFR when compared to other cases, but Coil X has an ideal coil shape, not an actual practice coil shape, which resulted in over-prediction. Coil A orientation was found to divert the flow better, towards the outlet branches compared to other orientations. Hence, Coil A enables lower VFR when compared to other orientations of FCL. Coil D allows greater VFR than other orientations of FCL. Earlier studies have shown that greater VM at the aneurysm neck region increases the chances of aneurysm recurrence after treatment [37]. Therefore, it is necessary to impede the flow through the aneurysm neck region. This is further corroborated by the residual flow volume (RFV) plots, as shown in Fig. 14. It can be noticed that the flow into the aneurysm is filled with velocity magnitude (VM) greater than 10 mm/s in an uncoiled aneurysm. Although coil X has the least RFV, it is overpredicting compared to the actual coil shape. Orientation of coil A, which is the actual coil shape, better diverts the flow towards the outlets than other orientations.

4.2 Vortical structures

To understand the nature of rotational tendency in the aneurysm region, vorticity variation in the basilar top region is plotted in Fig. 15. The influence of FCL orientations limits the generation of vorticity, while the walls of the inflow tube generate and convect the vorticity produced. During T2 and T3, there is vortical flow inside the aneurysm, which is shown in Fig. 15 (b and c); this vortical flow is blocked by the FCLs significantly. Coil A has significantly higher vorticity above coil area than Coil X during T2. The vorticity created by the actual coil shape is slightly higher than the ideal coil. The vorticity created at the center region of FCLs junction for Coil A is limited when compared to other regions. For Coils B, C, and D, the FCLs placed near the aneurysm wall region create higher vorticity than the FCLs that are placed at the aneurysm center.

4.3 Quantitative velocity distribution

Variation of VM along the central axis as well as on the left with an offset to central plane by 1.5 mm is plotted for all the cases. The variation in velocity along this line for the aneurysm (without coil) from the neck of the aneurysm during T1, T2, and T3 is shown in Fig. 16a and b respectively. The flow is more disturbed during T3 because of flow disturbance during the deceleration phase. Intra-aneurysmal VM is higher in aneurysm without coil; therefore, VM at the neck of the aneurysm during T1, T2, and T3 (no coil case) is used to normalize the VM at different orientations of FCLs during T1, T2, and T3 as shown in Figs. 17, 18, and 19 respectively.

Reduction in the intra-aneurysmal VM is more for Coil A than in other FCL orientations during T1, T2, and T3. This is primarily due to better flow blockage both into and out of the aneurysm. Reduction of intra-aneurysmal VM is more at the center of the aneurysm than the left and right side of the aneurysm after the insertion of FCLs during T1 and T2, as shown in Figs. 17 and 18, respectively. During T3, VM reduction on the left side is better than the central axis of the aneurysm, which is presented in Fig. 19. At the central axis of the aneurysm, Coil D allows higher VM than other FCL orientations during T1 and T3; during T2, Coil C allows higher VM inside the aneurysm. At the left and right side of the aneurysm, Coil D allows higher VM than other FCL orientations during T1, T2 and T3; but the difference between VM allowed by Coil D and Coil C is low. The difference between the VM of Coil A and Coil X shows the efficacy of the coil embolization process. Since Coil A accounts for the actual practice coil shape, which includes both the primary and secondary diameter of the embolic coil instead of the ideal coil shape (only the secondary diameter), it should be preferred. Suffice it to say, accounting for the primary and secondary coil details in the simulations would be highly meaningful in understanding the utility of coil shapes in actual practice.

4.4 Oscillatory shear index

Velocity variation in the vicinity of the wall results in gradients, which is exemplified as temporally varying shear stress. From CFD simulations, oscillatory shear index may be obtained as,

$$\begin{aligned} OSI = \frac{1}{2}\left( 1-\frac{\bigg |\int _{0}^{T}WSS_i dt\bigg |}{\int _{0}^{T}WSS_i dt}\right) \end{aligned}$$
(6)
Fig. 20
figure 20

Oscillatory shear index (OSI) distribution for three different (front, side and top) views of the aneurysm

Full size image

The oscillatory shear index (OSI) varies from 0 to 0.5, and it represents how much wall shear stress fluctuates during the course of a cardiac cycle [28, 38, 39], where T represents the cycle duration, and WSS\(_i\) represents the instantaneous wall shear stress vector. OSI distribution for all cases is shown in Fig. 20 for three distinct planes (XY, YZ, and XZ). As indicated in Fig. 20, OSI is lowest in aneurysms without coil, highest for Coil X. Note that low OSI is indicative of the expansile nature of the aneurysm, while higher OSI is highly desirable. However, it should be pointed out that Coil X is an ideal geometry and perhaps, resulted in an over-prediction. To this end, the FCL orientations with complete details may be particularly observed in Fig. 20. Coil A has a lesser OSI than Coil X; this means by considering the actual practice coil shape, there is a significant change in the OSI than the ideal coil shape. OSI distribution is higher wherever the flow is passing through the FCL and impinges on the aneurysm wall. This would in turn promote thrombus formation inside the aneurysm leading to flow stasis.

4.5 Hemodynamic simulations using a porous medium model

From the present simulations, it was observed that orientation for coil A is the most preferred configuration. Hence, further computations are performed for this orientation. Additionally, for the coil embolization, a coil having suitable coiling packing density and porous medium approximation is assumed for the hemodynamic simulations. Following our recent study [23], a coil packing density (PD) of 20\(\%\) was found to be optimum. This PD was used in the present study.

Fig. 21
figure 21

Flow features for an embolic coil-filled aneurysm with the framing coil and porous domain during peak systole. (a) Normal component of flow velocity above FCLs (1.85 mm above the neck plane). (b) Residual flow volume greater than 10 mm/s

Full size image
Fig. 22
figure 22

Average velocity variation over a cardiac cycle for various coil configurations with the embolized coil accounted as a porous medium

Full size image

4.5.1 Flow features

At a section of 1.85 mm above the neck plane and into the aneurysm, the Y-component of velocity in Fig. 21(a) indicates a clear reduction in the normal component of flow velocity. This range is intentionally kept between 0 and 5 mm/s. Furthermore, complete coiling of the aneurysm with 20\(\%\) packing density reduced the inflow velocity considerably. The volume flow rate of above 10 mm/s is plotted in Fig. 21(b) to visualize the influence of residual flow volume. The aneurysm filled with 20\(\%\) packing density allows minimal inflow with a much lower velocity.

Apart from the qualitative description, velocity distribution inside the aneurysm dome is quantified for different cases. The average velocity normal to the cross-section inside the aneurysm dome as a function of the cardiac cycle is shown in Fig. 22. Although the orientation of coil X enables lower average velocity than other cases, its cylindrical rod-like shape is too idealized. When compared with the actual embolic coil shape, Coil A allows lesser averaged velocity inside the aneurysm. Further placement of coil inside the aneurysm with 20\(\%\) packing density results in a substantial reduction in the average velocity.

4.5.2 Oscillatory shear index

The influence of coil packing density and FCL orientation with their combined influence is plotted for the oscillatory shear effects of pulsatility as shown in Fig. 23. The plot clearly indicates that the hemodynamic parameter has a minimal influence. A comparative assessment of this visual against Fig. 20 reveals that oscillatory shear influences are negligible for this framing coil orientation with the embolized coil. When the aneurysm is filled with a coil of 20\(\%\) packing density, the OSI developed in the aneurysm dome reduced significantly.

Fig. 23
figure 23

Variation of OSI after the aneurysm is completely filled with embolic coil as a porous medium, with FCL A as its orientation

Full size image

5 Summary

5.1 Conclusions

Aneurysms are of serious concern in cerebral blood circulation and reduction of intra-aneurysmal flow velocity is the primary goal of coil embolization. While porous medium-based coil embolization simulations provide an integral picture of the flow resistance and its relation to thrombus formation, it is important to study the resistance to flow, encountered at the neck plane. Hence, in the present study, numerical simulations are performed to analyze the effects of different orientations of the framing coil loop (FCL) on the intra-aneurysmal hemodynamics. A simpler approach is used to represent the actual embolic coil shape used in clinical practice, consisting of both primary and secondary diameter, instead of considering the ideal embolic coil shape. Actual practice coil shape for an embolic coil simulation provides an accurate result than considering an ideal rod-like coil shape. From the present simulations, it was observed that the FCL orientation strongly influences the reduction of intra-aneurysmal flow velocity that facilitates thrombus formation. Reduction in velocity magnitude was higher in the case of Coil A orientation compared to B, C, D orientations. This was further corroborated through the momentum impeded by the framing coils, by plotting the volume flow rate inside the aneurysm and residual flow volume. Higher values of OSI were observed for Coil A orientation (highest for Coil X—ideal shape), which is indicative of better likelihood of thrombus formation. From the hemodynamic simulations performed on FCL’s (X, A, B, C, D), orientation of Coil A is recommended based on velocity, vorticity, volume flow rate, OSI etc. Furthermore, for the Coil A orientation, coil embolization effects are studied using the porous medium simulations. An optimal packing density of 20\(\%\) was assumed for the porous medium-based simulations using the FCL Coil A orientation. The findings from this study provide useful pointers to the clinicians in analyzing various FCLs to achieve a desired outcome on how to reduce intra-aneurysmal flow velocity.

5.2 Limitations

The CFD simulations performed in this study have several limitations when compared to real-life coil embolization and blood flow. The aneurysm wall and FCLs were assumed to be rigid. Placement of FCLs was designed in an orderly manner. However, while performing coil embolization, the neurosurgeon may not have such orderly and finer control on the FCL’s. Hence, the cases may be seen as particular instances of actual coil embolization. Interaction of blood flow with the framing coil was not considered during FCLs placement near the aneurysm neck region. Although the porous medium-based simulations overcome some of these limitations, this approach ignores the tortuous filling of the coil distribution. The above-mentioned limitations do not affect the investigation since the main goal of this work is to find out the framing coil orientation, which facilitates flow stasis.