Fast and accurate line detection with GPU-based least median of squares

Abstract

We propose an accurate and efficient 2D line detection technique based on the standard Hough transform (SHT) and least median of squares (LMS). We prove our method to be very accurate and robust to noise and occlusions by comparing it with state-of-the-art line detection methods using both qualitative and quantitative experiments. LMS is known as being very robust but also as having high computation complexity. To make our method practical for real-time applications, we propose a parallel algorithm for LMS computation which is based on point-line duality. We also offer a very efficient implementation of this algorithm for GPU on CUDA architecture. Despite many years since LMS methods have first been described and the widespread use of GPU technology in computer vision and image-processing systems, we are unaware of previous work reporting the use of GPUs for LMS and line detection. We measure the computation time of our GPU-accelerated algorithm and prove it is suitable for real-time applications. Our accelerated LMS algorithm is up to 40 times faster than the fastest single-threaded CPU-based implementation of the state-of-the-art sequential algorithm.

1 Introduction

Detecting lines in image data are a basic task in pattern recognition and computer vision, and it is used for both data reduction and pre-processing before higher level visual inference stages. Most existing line detection methods are variants of the SHT. The reader is referred to [22] for a recent survey on HT and its variants.

Despite its popularity, SHT has some well-known shortcomings in that quantization errors appear in both the input image and in the voting accumulator. The higher the resolution of the voting accumulator, the more adverse the effect of quantization errors will be [33]. In a high-resolution voting accumulator, each feature point votes for many cells. This causes the spreading of votes on a large area with no distinct single peak, which, in turn, leads to inaccurate peak detection. Many methods have been devised to overcome this problem (see Sect. 2 for more detail). High-resolution SHT also suffers from high memory and computation complexity. To address the time performance problem, several randomization variants have been suggested and special hardware has been used to ensure fast implementation.

Robust estimators are used to detect lines in noisy images due to their ability to handle outlying data points. The robustness of these estimators is measured by their breakdown point, which is the fraction of outlying data points that are required to corrupt the estimator’s accuracy. Least median of squares (LMS) is one such robust method. Intuitively, if more than half of the points are inliers, then LMS cannot be affected by the higher order statistics residuals. In this case, the outliers can be arbitrarily far from the estimate without disturbing the estimate. The LMS estimator has been used extensively in many applications in a wide range of fields and it is considered to be a standard technique in robust data analysis. To date, and despite the many years since its original release, the Rousseeuw LMS regression (line) estimator [27] remains the most popular and well-known $50\%$ breakdown-point estimator. Despite this robustness, LMS is seldom used in practical applications for line detection due to its high complexity requirements.

Our goal in this work is to overcome the limitations of SHT and to devise a line detection method that is fast, accurate, and resilient to noise. Our contribution is as follows: we suggest a novel 2D line detector based on low-resolution SHT and LMS. To make LMS practical in real world applications, we reduce its computation time dramatically using a parallel algorithm implemented on the graphical processing unit (GPU). We prove that our compute unified device architecture (CUDA)-based algorithm is faster than a single-thread CPU implementation of the fastest sequential algorithm, by up to a factor of 40. Beyond its use here for line detection, our fast LMS implementation is highly applicable on its own in a wide range of applications, for computer vision, image processing, and robust statistics. To encourage reproducible research, we have shared our implementation of the algorithm online https://github.com/ligaripash/CudaLMS2D.git

2 Related work

SHT high computational demand has led to an extensive effort to reduce its computational complexity by various means. Hardware acceleration of SHT is offered by many authors using various hardware architectures. For example, Refs. [21] and [15] suggest a HT system accelerated by FPGA and [17, 34] propose an acceleration algorithm based on the GPU. HT can also be accelerated using randomization: the two most popular variants are randomized HT [35] and probabilistic HT [18]. These methods trade a small amount of detection accuracy for improved computation speed. Although they are fast, these methods are not robust against noise (see [22]).

Sub-image methods have also been used to manage HT high computational demand. These methods increase the voting unit from one pixel in SHT to a collection of pixels, forming a sub-image; as in [14, 29]. Among this class of HT variants, the work by [11] stands out in both accuracy and speed. Consequently, we use this as a baseline method in our experiments.

SHT also suffers from an accumulator peak localization problem. Uniform parameter sampling along with image quantization, sensor noise, and optical distortion cause the votes in the accumulator to spread. Consequently, locating the peak becomes a challenging task. The problem is aggravated when $\delta \rho$ and $\delta \theta$ become smaller [22] (see Algorithm 1 for the definitions of these parameters). The accumulator votes tend to form a typical butterfly pattern and many scholars have tried to analyze this pattern and find the correct peak [1, 12, 16].

We call our method the Hough transform–Cuda-based least median of squares (HT–CLMS) line detection method. In our HT–CLMS solution, the accumulator resolution is defined by the line separation requirements and not by line accuracy as in SHT. This facilitates the use of a coarse HT accumulator that is fast, consumes a small amount of memory, and does not suffer from quantization problems.

LMS algorithms Stromberg [32] provided one of the early methods for exact LMS with a complexity of $O(n^{d+2}\log n)$, where d is the dimension of the points. More recently, Erickson et al. [9] describe a LMS algorithm with a running time of $O(n^d\log n)$.

Souvaine and Steele [30] designed two exact algorithms for LMS computation. Both algorithms are based on point-line duality. The first constructs the entire arrangement of the lines dual to the n points, and requires $O(n^2)$ time and memory space. The second sweeps the arrangement with a vertical line, and requires $O(n^2\log n)$ time and O(n) space. Edelsbrunner and Souvaine [8] have improved these results and give a topological sweep algorithm that computes the LMS in $O(n^2)$ time and O(n) space. To our knowledge, however, no GPU-based or other parallel algorithm for computing LMS regression has since been proposed.

Alongside these theoretical results, recent maturing technologies and plummeting hardware prices have led massively parallel GPUs to become standard components in consumer computer systems. Noting this, we propose an exact, fast, CUDA-based, parallel algorithm for 2D LMS computation. Our method provides a highly efficient and practical alternative to the traditional, computationally expensive LMS methods.

3 Our proposed line detection approach

Our proposed approach addresses the two basic problems with SHT:

• Its inaccuracy in high resolution due to peak spreading, and

• its high computational cost in the voting process when using a high-resolution accumulator.

We propose to address both of these issues by following up the process performed by the SHT with a LMS method, as described in Algorithm 1 and in Fig. 1

Fig. 1

Block diagram of our HT–CLMS (please see Algorithm 1). The input noisy meteor image is at the top left. The input image goes through the canny edge detector. At the next stage, a low-resolution SHT is applied and local maxima are located. For each maximum a matching sleeve is located in the edge map (right column, middle row). All edge points in the sleeve are extracted and fed to our fast parallel CLMS algorithm which recovers the correct meteor line in spite of many outliers

The rational here is simple: we use a low-resolution accumulator to avoid the peak splitting phenomenon that is attributed to high-resolution SHT [33]. Thus, each coarse cell will contain votes from all of the feature points that reside on this line, as well as point votes due to noise or other line structures. As long as the true line votes comprise the majority of the votes in that cell, LMS guarantees that none of the outlying data will corrupt the line estimate.

To illustrate this point, Fig. 2 shows a line segment sampled with probability 0.5 with random noise. The accumulator resolution is coarse with $\delta \rho = 20, \delta \theta = 20.$ All of the points that voted for the peak accumulator cell are marked in purple. Notice that the line could be accurately recovered in spite of many outliers.

The low resolution here determines the minimal separation between the lines and not the detection accuracy; that is, if two lines exist in the input image $(\rho _1, \theta _1)$ and $(\rho _2, \theta _2)$, and the accumulator bin size is $({\text {d}}\rho , {\text {d}}\theta )$, then if $|\rho _1 - \rho _2| < {\text {d}}\rho$ and $|\theta _1 - \theta _2| < {\text {d}}\theta$, and then both lines will cast votes to the same cell and after the LMS operation only one line will be detected.

HT–CLMS can be integrated with other HT variants that use accumulator peaks to recover the feature points voting for the line (e.g., the progressive probabilistic Hough transform (PPHT) [13]). This can be done by replacing the regular least square used by these methods with LMS.

Our experiments with this method show it to be very robust and accurate. The current state-of-the-art complexity for LMS computation, demonstrated by Eddelsbrunner and Souvaine [8], has $O(n^2)$ time complexity. Such computational load is inadequate for real-time applications, thereby prohibiting the use of LMS for line detection. To mitigate this problem, we show how LMS can be efficiently computed on a GPU.

Fig. 2

Synthetic image with random noise probability $= 0.002$ and line sampling probability $= 0.5$. The purple circles are points which voted for the Hough cell with maximum votes. $\delta \rho = 20$, $\delta \theta = 20$. The LMS line for the purple points is marked in red. The SHT line is marked in green. Less than half of the supporting features are attributed to noise and so our CLMS regression estimation is accurate

3.1 Fast CUDA method for 2D LMS (CLMS)

Our algorithm is based on point-line duality and searching line arrangements in the plane. Point-line duality has been shown to be very useful in many efficient algorithms for robust statistical estimation problems (e.g., [5, 6, 8, 9, 30]). We begin by offering a brief overview of these techniques and their relevance to the method presented in this paper.

Fig. 3

LMS geometric interpretation: computing an LMS regression line is equivalent to finding a slab that contains at least half the input points and whose intersection with the y-axis is the shortest. d denotes the LMS

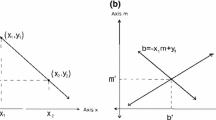
Geometric interpretation of LMS By definition, the LMS estimator minimizes the median of the squared residuals. Geometrically, this means that half of the points reside between two lines, parallel to the estimator. Assume d to be the least median of squares, one of the lines is in distance $\sqrt{d}$ above the estimator, and the other is in distance $\sqrt{d}$ below the estimator. The area enclosed between these lines is called a slab. Computing the LMS estimator is equivalent to computing a slab of minimum height. The LMS estimator is a line that bisects this slab, see Fig. 3. Steel and Steiger [31] showed that for the LMS slab, one of its bounding lines must contain at least two input points and the other must contain at least one input point. Based on this fact and point-line duality, finding the LMS slab dualizes to finding the minimum vertical segment which intersects n/2 lines and hangs on an intersection of two lines on one end and on a dual line on the other end [31]. Vertical segments in the dual are called bracelets and the minimum length bracelet that intersects n/2 lines is called the LMS bracelet (see Fig. 4 for an illustration of these concepts.)

Our proposed parallel LMS The current state-of-the-art algorithm for LMS computation was purposed by Eddelsbrunner and Souvaine [8]. They proposed a topological sweep approach which traverses the dual-line arrangements and finds the LMS bracelet in $O(n^2)$ and O(n) space. Noting that their sweep line technique is sequential by nature and that the computations of bracelets are independent on one another, we propose to compute all of the bracelets that hang on an intersection point in parallel, and we then use the parallel reduce operation to find the minimum length bracelet. The algorithm pseudo-code is presented in Algorithm 2.

Fig. 4

LMS in the dual plane. The bottom figure depicts the primal plane with a set of points and the LMS slab. The top figure depicts the dual plane. The black points dualize to black lines in the upper figure. The LMS slab passes through the red points in the primal which correspond to red lines in the dual plane. The intersection points of the red lines in the dual correspond to the LMS slab lines in the primal. Finding the LMS slab in the primal plane dualizes to finding the minimal vertical segment that intersects n/2 lines (the LMS bracelet)

Algorithm correctness As proven by Steel and Steiger [31], it is assured that the minimum bracelet has one end on the intersection of two lines. The algorithm exhaustively searches for all bracelets that have this property and, therefore, must find the global minimum bracelet. The algorithm is consequently correct.

Algorithm performance Assuming a parallel random access machine (PRAM) model [26] and a parallel machine with unbounded number of processors, parallel computation of all the points duals (lines 1–3 in Algorithm 2) takes O(1) time (each processor computes one point dual).

Computing the intersection points of all line pairs (lines 4–7) also requires O(1) time (each processor computes the intersection point of one pair of lines). For each intersection point, we find the intersection of all the lines with a vertical line that passes through the intersection point (lines 9–12). This is also a O(1) time task. A bitonic parallel sorter (line 13) takes $O({\log }^2n)$ (see Batcher [2]). On the final step, a parallel reduction (line 18) is performed on an array in the size of the number of intersection points, which is $O(n^2)$. This parallel reduction takes $O(\log n)$ time. The overall time complexity, therefore, equals the time of the bitonic sorter: $T_\infty = O({\log }^2n)$. This should be compared to the optimal sequential algorithm, which requires $O(n^2)$ time.

The total work required by the algorithm is sorting n elements for each of the $O(n^2)$ intersection points, which amounts to $O(n^3\log n)$ computations. This also equals the time complexity $T_1$ of the algorithm running on one processor. On a machine with a bounded number of processors, the time complexity is asymptotically equal to $T_1$; hence, for large input size, the parallel version is expected to do worse than the optimal $O(n^2)$ sequential algorithm but for practical input size for line detection we demonstrate that the parallel version is 20–40 times faster than the single threaded state-of-the-art.

Finally, the space complexity of our method is $O(n^2)$ because we must save all of the intersection points in an array. Depending on GPU memory, this currently restricts LMS computation to no more than a few thousand points. This limitation can be mitigated by working on small batches of intersection points. We leave this extension for future work.

3.2 Details of the CUDA implementation

In accordance with Sanders and Kandrot [28], we set the following design goals so that we can achieve optimal performance using the CUDA platform:

• Maximize occupancy,

• Memory coalescence—adjacent threads call adjacent memory locations, and

• bank conflict free, shared memory access pattern.

The first part of Algorithm 2 (line 8) requires us to calculate the intersection point of each pair of lines. To do that in CUDA, we create the following thread hierarchy. Each thread block contains $8\times 8$ threads and each grid contains a $\frac{\left| L \right| }{8}\times \frac{\left| L \right| }{8}$ thread block. This creates the thread structure that is displayed in Fig. 5.

Fig. 5

The thread grid for computing line intersections. Each thread block has $8\times 8$ threads. In the grid there are $\frac{n}{8}\times \frac{n}{8}$ thread blocks. Thread $t_{i,j}$ calculates the intersection of line i with line j. $n = \left| {\mathbf {L}}\right|$

Here, memory access is coalesced as thread $t_{i,j}$ reads line ${\mathbf {l}}_i$ and ${\mathbf {l}}_j$ while the next thread in the row $t_{i,j+1}$ reads ${\mathbf {l}}_i$ and ${\mathbf {l}}_{j+1}$, which resides right next to ${\mathbf {l}}_j$ in the line array. To prevent redundant access to global memory, threads in the first row and first column of each thread block read the respected lines from global memory to the shared memory of the block. This saves $2\times (64 - 2\times 8) = 96$ global memory access per block. To avoid computing the line intersections twice, only threads $t_{i,j}$, where $i> j$ perform the computation while the rest do nothing. Each thread computes the intersection of two lines in ${\mathbf {L}}$ with the vertical line passing through its intersection point. The intersection points are stored in shared memory.

In the second part of the algorithm, we compute the bracelet that hangs on every intersection point that we found earlier (see Algorithm 2, lines 8–17). To this end, we assign a thread block to compute each bracelet (see Fig. 6). Thread block dimension is set to $(1, \frac{\left| L \right| }{2})$. Each thread computes the intersection points of two lines from ${\mathbf {L}}$, where the vertical line which passes through the intersection point assigned to the thread block. Later, the thread block performs a fast parallel bitonic sort [24]. A parallel bitonic sort operates only on power of two data items and so we allow only power of two input size. When the input size does not meet this requirement, this limitation can be easily dealt with by padding. The thread grid has dimension (k, 1), where k is the number of point intersections ($k = \frac{n \times (n - 1)}{2}$).

Fig. 6

The thread structure for bracelet calculation per intersection point. Each thread block computes the bracelet for its designated intersection point. The thread grid contains $\frac{n\times (n-1)}{2}$ thread blocks. Each thread block contains n threads

4 Implementation and results

To evaluate our method, we performed four types of experiments:

• 1. Quantitative experiments to assess the accuracy of HT–CLMS recovered line parameters using synthetic images (Sect. 4.1).

• 2. Qualitative experiments with real world images and various line detection applications (Sect. 4.2)

• 3. Quantitative tests on real images (Sect. 4.3).

• 4. Runtime evaluation of CLMS (Sect. 4.4).

4.1 HT–CLMS accuracy on synthetic images

We have created four sets of images. Each set contains 500 binary, synthetic images with $200\times 200$ pixels. Each image contains one line segment with randomized end points. Random noise is added on various levels and used to perturb pixels on the lines. A varying fraction of the segment points are moved one pixel in a direction perpendicular to the segment. A sample input image is shown in Fig. 6. The normal parameters $(\theta , \rho )$ are calculated and saved as ground truth. Each set is characterized differently by a combination of three parameters:

• n: The number of noise pixels in the image

• q: Hough space quantization resolution ($\delta \rho = \delta \theta = q$),

• t: The fraction of point shifted one pixel in a direction perpendicular to the segment.

The input images are created with different amounts of random noise and line perturbations. We have created four noise categories:

• No noise ($n = 0$, $t = 0$),

• Low noise ($n = 400$, $t = 0.2$, $\hbox {PSNR}= 20.00$ dB),

• Medium noise ($n = 700$, $t = 0.25$, $\hbox {PSNR} = 17.57$ dB),

• High noise ($n = 1000$, $t = 0.3$, $\hbox {PSNR} = 16.02$ dB).

We compare four line detection methods:

• 1. SHT We measure the detection accuracy with three accumulator quantization values: low quantization ($q = 0.5$), medium quantization ($q = 1$) and high quantization ($q = 3$). We use the standard OpenCV implementation for this method [3].

• 2. Least square fitting (LSF) This methods uses ordinary least square to fit a line to the pixels which voted to the line defined by SHT. We use two quantization levels: $q = 1$ and $q = 3$.

• 3. KHT A popular HT-based line detection method [11]. The algorithm was tested with the parameters recommended by its authors. The implementation for this algorithm is supplied by others [10].

• 4. HT–CLMS Our proposed method.

Table 1 Comparison of the accuracy of the line detection methods

Table 2 p values of two-sample paired t test

We test all algorithms with a range of typical parameters. The line parameters estimated by each algorithm were compared with the ground truth, and the detection errors in both $\rho$ and $\theta$ were recorded. The results are given in Table 1. To statistically validate the superior accuracy of our method, we conduct a paired two-sample t-test between the $\rho$ error distribution of HT–CLMS and the $\rho$ error distribution of every other method. The null hypothesis is that the error distributions are the same. The p-values depicted in Table 2 show that given the null hypothesis the probability of the data is negligible, hence we reject the null hypothesis and conclude that HT–CLMS accuracy is significantly higher than the accuracy of every other method in every noise level.

Several interesting observations can be made from our results.

First, for an image with no noise, LSF is the most accurate. This is probably due to the fact that line quantization errors spread evenly with respect to the ideal line thus errors cancel out resulting in a very accurate line estimation. Second, KHT is less accurate than SHT with ${q}=1$. Next, the accuracy of LSF (${q}=1$) degrades severely as noise level increases. Also, high-resolution HT (${q}=0.5$) has comparable accuracy to HT (${q}=1$) due to peak spreading. Finally, our HT–CLMS is the most accurate method when adding noise in all levels. In fact, robustness to noise and line estimation parameters hardly changes with respect to noise levels.

To better illustrate our findings, we show the accuracy measured on 50 lines in high- and medium-noise conditions. Specifically, Fig. 7 provides detection errors for high-noise images and Fig. 8 for medium-noise images.

Real-time applications optimize for both accuracy and computation time. Figure 9 illustrates the joint accuracy and computation time for the various algorithms. From this diagram, it is evident that HT–CLMS exhibits good trade-off between computation time and accuracy.

4.2 Qualitative results on real world images

We test our line detection method on the following three applications. In all of these applications, ground truth was not available for measuring performances.¹ For all of these applications, the accumulator cell radial size (${\text {d}}\rho$) and polar size (${\text {d}}\theta$) were chosen using the following rational: as explained in Sect. 3, the points taken for CLMS regression are the points that voted for an accumulator cell. If the cell is large (a low-resolution accumulator) more points could fall into any one call and vice versa. If the cell is too large (resolution is too low) a single cell may be assigned points from separate lines and this will corrupt the LMS estimate. If the cell is too small then cells may not be assigned sufficiently many points to produce an accurate LMS line estimate. In our tests, we, therefore, set the accumulator resolution values (accumulator cell size upper bound) to be the minimal radial and polar distances between the lines we wish to detect.

• Perseids meteor detection This is a problem of interest to the planetary and space communities [23]. Meteor images typically suffer from low-light conditions. To locate the trail of light left by meteorite, we threshold the input image and then detect the longest line in the image. The meteor images contain one meteor per image hence ${N}=1$. Perseids images usually contain only one line (perseid) per image so the ${\text {d}}\rho$ and ${\text {d}}\theta$ can be arbitrarily large. The values ${\text {d}}\rho = 2 \,\, {\text{and}}\,\, {\text {d}}\theta = 2$ were used as they are high enough to capture all the pixels which belong to the perseids but higher values work equally well. Our results are provided in Fig. 10.

• Horizon detection This problem often occurs when analyzing maritime video data. The input image is pre-processed with the Canny edge detector and only the longest line is reported (${N}=1$). As in the Perseids application these images contain only one true line (the horizon line). and hence the values ${\text {d}}\rho = 2\,\, {\text{and}}\,\, {\text {d}}\theta = 2$ were chosen by the same considerations. The results are provided in Fig. 11. The proposed line detection method finds horizon lines robust despite sea waves and other sources of noise which can clutter image edges.

• Road lane detection in low-light conditions To report our results for this important application, we used the image sequence published as Set 1 in EISATS [19]. This set is a night vision image sequence taken from a moving car. As expected, this night vision sequence is characterized by low light and high noise. Its images are, therefore, challenging test cases for our robust line detection method. For this application, we used the canny edge detector on the bottom half of the image (which typically contains the road) and then extracted the four longest lines (${N}=4$) using our HT–CLMS method. We have found that for this application the polar and radial distances between the closest lines we wish to detect is more than (${\text {d}}\rho = 2, {\text {d}}\theta = 2$) so these values were chosen. The results are depicted in Fig. 12

Fig. 7

Comparison of detection error in high-noise images

Fig. 8

Comparison of detection error in medium-noise images

Fig. 9

Average error in $\theta$ vs. computation time for various line detection algorithms on images with high-noise values. HT–CLMS is both fast and accurate

Fig. 10

Examples for Perseids meteorite detection in noisy images

Fig. 11

Examples for horizon detection

Fig. 12

Examples for lane detection in low-light conditions

4.3 Quantitative real world results

We used two data sets to quantitatively test out HT–CLMS. The first data set was provided by Candamo et al. [4]. It contains 5576 manually annotated images of thin obstacles such as cable power lines and wires. Some of the samples are challenging as can be seen in Fig. 13. We tested both our HT–CLMS and the popular KHT algorithm on this data set. We consider a ground truth line as detected by an algorithm if its normal parameters error $\theta _{\text {err}}$ and $\rho _{\text {err}}$ are below a fixed threshold. We collected line errors only when the line has been detected by both HT–CLMS and KHT. The cumulative error distribution (CED) graph for $\theta _{\text {err}}$ is shown in Fig. 14. HT–CLMS is more accurate than KHT on this dataset.

Fig. 13

Sample from the thin obstacle dataset [4]

Fig. 14

Cumulative error distribution of $\theta _{\text {err}}$ for HT-CLMS and KHT for the thin obstacle dataset [4]

The second data set we used is the York Urban Line Segment Database [20]. These images include both indoor and outdoor scenes. In each image, the vertical and horizontal lines are manually labeled. Note that manual labeling has some discrepancy relative to the edges found by an edge detector, as demonstrated in Fig. 15, the main discrepancy is shown to be in the radial direction. To facilitate meaningful measurements we manually re-annotated the ground truth data.

Figure 16 provides an example test image with the ground truth line segments marked in blue and estimated lines in red. We test HT–CLMS on this image and compare the results with those published by Xu et al. [35] using their statistical line segment method (SLS) for line detection. Notice that some ground truth lines are not detected, typically due to of weak edges. Also, some detected lines are not marked as ground truth (only horizontal and vertical lines are marked). To evaluate accuracy, we, therefore, compare only lines that are both labeled as ground truth and which are detected by both HT–CLMS and SLS.

For each labeled line segment, we recover its normal line parameters, $(\rho , \theta )$, and compare them to the line parameters estimated by HT–CLMS and SLS. The results are given in Table 3. Our HT–CLMS method performs much better than SLS with average $\theta$ error of 0.11 compared with 0.35 of SLS and average $\rho$ error of 0.99 compared with 2.92 of SLS.

Fig. 15

Ground truth labeling error. The blue GT is shifted one pixel in the $\rho$ direction relative to the true edge. HT–CLMS compute accurate estimate

Fig. 16

Sample image from the York Urban Line Segment Database. HT–CLMS lines are marked in red. Ground truth line segment is marked in blue

Table 3 Comparison of HT–CLMS line detection method for the image in Fig. 16 versus the marked ground truth and the line segment computed by the SLS method by Xu at al. [35]

4.4 Runtime evaluation of the CLMS

Our line detection algorithm is based on a fast computation of LMS using the CLMS method. Our implementation of the CLMS method, described in Algorithm 2, is publicly available online.² We have compared it with the state-of-the-art, topological sweep algorithm of Eddelsbrunner and Souviene [8]. A software implementation of a variant of this algorithm is given by Rafalin [25]. In our comparison, both algorithms were provided with the same random point set of sizes 128, 256, and 512 points. The correctness of our algorithm is quantitatively verified by comparing its output for each point set with the output of the topological sweep method.

Table 4 Performance comparison between the sequential topological sweep algorithm of [8] implemented by [25] (Top Sweep), and our own CLMS implementation

Fig. 17

Runtime comparison between Top Sweep [25]—the state-of-the-art LMS, sequential algorithm—running on a CPU and our parallel algorithm, CLMS, running on a GPU. Dashed lines represent theoretical, best case, estimates of computation time for the Top Sweep, if it were parallelized to the use of two, four, or eight threads. Importantly, as far as we know, Top Sweep has not been parallelized and cannot be executed by more than a single thread

Our results are reported in Table 4 and Fig. 17. Evidently, in all cases the speedup factor of our proposed method was substantial. Note how the speedup factor decreases as input point set size increases. This occurs because the Top Sweep algorithm has an asymptotically lower complexity (see Sect. 19). These results suggest robust estimation is completely feasible in real-time, image-processing applications.

5 Conclusions and future work

Despite the ubiquitous use of line detection methods in image processing and computer vision systems, and the many years since these methods were first introduced, very little has changed in how lines are detected or the runtime of line detection implementations. In this paper, we propose a method which is both more robust (higher breaking point) and faster than existing methods. Key to our approach is the observation that the GPU processors—now standard fixtures in many computer systems—are well suited for efficient LMS computation.

Based on this observation, we propose a line detection algorithm designed using SHT and LMS. We show that our algorithm is very robust to noise. Using CUDA, we describe an LMS implementation that is 20–40 times faster than a single-threaded CPU implementation of the fastest LMS algorithm described in the literature. We tested HT–CLMS extensively and compared its results with a variety of existing line detection algorithms. Our results demonstrate that accurate and highly robust line detection are both feasible even for real-time applications. Importantly, the properties of LMS have been well known for some time and GPU hardware is widespread in standard computer vision and image-processing systems. Still, we are unaware of previous reports demonstrating the use of GPUs for accelerated line detection using accurate LMS methods.

Future work A natural extension of this work is the detection of 3D lines in a 3D point cloud. The concept of point-line duality used as a the foundation for our CLMS algorithm can be easily extended to point-plane duality in 3D space. This extension can have important applications in computer graphics systems, where 3D point cloud data are commonplace.

Another interesting direction for future work is the application of the idea of fast searching in the line arrangement of the dual space to solve the maximal margin clustering problem: At the core of our CLMS algorithm, we conduct a parallel search for the minimal bracelet in the dual plane—a minimum length slab that intersects n/2 lines. If we search for a minimal slab that intersects no lines at all, we find a solution to the maximal margin clustering problem which plays a significant role in unsupervised learning and has high computational complexity. This problem can thus benefit from a parallel acceleration approach similar to the one proposed here.

Finally, our accelerated CLMS algorithm can be also be used as a building block for other applications where fast robust regression is needed. We plan to explore such applications in future work.