Abstract
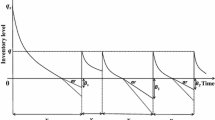
Common characteristics of inventory systems include uncertain demand and restrictions such as budgetary and storage space constraints. Several authors have examined budget constrained multi-item stochastic inventory systems controlled by continuous review policies without considering marginal review shortage costs. Existing models assume that purchasing costs are paid at the time an order is placed, which is not always the case since in some systems purchasing costs are paid when order arrive. In the latter case the maximum investment in inventory is random since the inventory level when an order arrives is a random variable. Hence payment of purchasing costs on delivery yields a stochastic budget constraint for inventory. In this paper with mixture of back orders and lost sales, we assume that mean and variance of lead time demand are known but their probability distributions are unknown. After that, we apply the minimax distribution free procedure to find the minimum expected value of the random objective function with budget constraint. The random budget constraint is transformed to crisp budget constraint by chance-constraint technique. Finally, the model is illustrated by a numerical example.
Similar content being viewed by others
References
Ben-Daya M., Hariga M.: Integrated single vendor single buyer model with stochastic demand and variable lead-time. Int J. Product. Econ. 92, 75–80 (2004)
Burgin T.A.: Inventory control with normal demand and gamma lead time. Oper. Res. Quart. 23(1), 73–80 (2007)
Ben-Daya M., Raouf A.: Inventory models involving lead time as a decision variable. J. Oper. Res. Soc. 45(5), 579–582 (1994)
Craven B.D.: Modelling inventories in a network. Optim. Lett. 1(4), 401–406 (2007)
Carlson P.G.: An alternative model for lead-time demand: continuous review inventory systems. Decision Sci. 13, 120–128 (1982)
Chu P., Yang K.L., Chen P.S.: Improved inventory model with service level and lead time. Comput. Oper. Res. 32, 285–296 (2005)
Chang H.C., Ouang L.Y., We K.S., Ho C.H.: Integrated vendor–buyer cooperative inventory models with controllable lead time and ordering cost reduction. Eur. J. Oper. Res. 170, 481–495 (2006)
Chen C.K., Chang H.C., Ouyang L.Y.: A continuous review inventory model with ordering cost dependent on lead time. Int. J. Inform. Manage. Sci. 12(3), 1–13 (2001)
Yano C.A.: New algorithms for (Q,r) system with complete backordering using a fill-rate criterion. Naval Res. Logistics Quart. 32, 675–688 (1985)
Charnes A., Cooper W.W.: Chance constrained programming. Manage. Sci. 6, 73–79 (1959)
Das C.: Explicit formulas for the order size and reorder point in certain inventory problems. Naval Logistics Quart. 23, 120–128 (1976)
Eryan A., Kropp D.H.: Effective and simple EOQ-like solutions for stochastic demand periodic review systems. Eur. J. Oper. Res. 180, 1135–1143 (2007)
Encyclopedia of Optimization, 2nd edn. An online version is available at http://www.springer.com/mathematics/book/978-0-387-74760-6
Hadley G., Whitin T.M.: Analysis of Inventory Systems. Prentice-Hall, Englewood Cliffs (1963)
Tinarelli G.U.: Inventory control: models and problems. Eur. J. Oper. Res. 14, 1–12 (1983)
Gallego G., Moon I.: The distribution free newsboy problem review and extension. J. Opl. Res. Soc 44(8), 825–834 (1993)
Haris F.: Operations and cost (Factory Management Series). A.w Shaw Co., Chicago (1915)
Wagner H.M.: Research portfolio for inventory management and production planning systems. Oper. Res. 28(3), 445–475 (1980)
Geunes J., Pardalos P., Romeijn E.: Supply Chain Optimization: Applications and Algorithms. Kluwer, Dordrecht (2002)
Parker L.L.: Economical Reorder quantities and reorder points with uncertain demand. Naval Res. Logistics Quart. 11(4), 351–358 (1964)
Liao C.J., Shyu C.H.: An analytical determination of lead time with normal demand. Int. J. Oper. Product. Manage. 11, 72–78 (1991)
Mood A.M., Graubill F.A., Boes D.C.: Introduction to the Theory of Statistics. Mc Graw-Hill Book Co, New York (1974)
Mayer P.L.: Introductory Probability and Statistics Application, pp. 241–242. Addison-Wesley, New York (1965)
Ord J.K., Bagchi U.: The truncated normal-gamma mixture as a distribution of lead time demand. Naval Res. Logistics Quart. 30, 359–365 (2006)
Ouyang L.Y, Yeh N.C., Wu K.S.: Mixture inventory modelwith backorders and lost sales for variable lead time. J. Oper. Res. Soc. 47, 829–832 (1996)
Ouyang L.Y., Chuang B.R.: Mixture inventory model involving variable lead time and controllable backorder rate. Comput. Indust. Eng. 40, 339–348 (2001)
Park C.: An analysis of the lead time demand distribution derivation in stochastic inventory systems. Int. J. Prod. Econ. 105, 263–272 (2007)
Pardalos, P.M., Resende, M. (eds): Handbook of Applied Optimization. Oxford University Press, Oxford (2002)
Pardalos P.M., Tsitsiringos V.: Financial Engineering, Supply Chain and E-commerce. Kluwer, Dordrecht (2002)
Brown R.G., Gerson G.: Decision Rules for Inventory Management. Holt, Rinehart and Winston, New York (1967)
Ağralı S., Geunes J.: A single-resource allocation problem with Poisson resource requirements. Optim. Lett. 3(4), 559–571 (2009)
Tersine R.J.: Principles of Inventory and Materials Management. North Holland, New York (1982)
Bagchi U., Hayya J., Chu C.: The effect of lead-time variability: the case of independent demand. J. Oper. Manage. 6(2), 159–177 (1986)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Kundu, A., Chakrabarti, T. A multi-product continuous review inventory system in stochastic environment with budget constraint. Optim Lett 6, 299–313 (2012). https://doi.org/10.1007/s11590-010-0245-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11590-010-0245-3