Skip to main content
Springer Nature Link
Log in

Convergence analysis for the modified spectral projected subgradient method

  • Original Paper
  • Published:
Optimization Letters Aims and scope Submit manuscript

Abstract

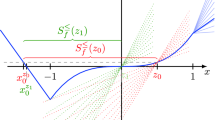
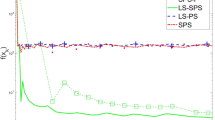
In a recent paper, the spectral projected subgradient (SPS) method was introduced by Loreto et al. for the minimization of a non-differentiable convex piece-wise function, and extensive numerical experimentation showed that this method was very efficient. However, no theoretical convergence was shown. In this paper, a modified version of the spectral projected subgradient (MSPS) is presented. The MSPS is the result of applying to SPS the direction approach used by spectral projected gradient version one (SPG1) proposed by Raydan et al. MSPS presents stronger convergence properties than SPS. We give a comprehensive theoretical analysis of the MSPS and its convergence is shown under some mild assumptions. The proof uses the traditional scheme of descent distance to the optimal value set, and a non-monotone globalization condition is used to get that distance instead of the subgradient definition. To illustrate the behavior of MSPS we present and discuss numerical results for set covering problems.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Barzilai, J., Borwein, J.M.: Two point step size gradient methods. IMA J. Numer. Anal. 8, 141–148 (1988)

    Article  MATH  MathSciNet  Google Scholar 

  2. Beasley, J.E.: Or-library: distributing test problems by electronic mail. J. Oper. Res. Soc. 41, 1069–1072 (1990)

    Article  Google Scholar 

  3. Bertsekas, D.P.: On the Goldstein–Levitin–Polyak gradient projection method. IEEE Trans. Autom. Control 21, 174–184 (1976)

    Article  MATH  MathSciNet  Google Scholar 

  4. Bertsimas, D., Tsitsiklis, J.N.: Introduction to Linear Optimization. Athena Scientific, Belmont (1997)

    Google Scholar 

  5. Birgin, E.G., Martinez, J.M., Raydan, M.: Nonmonotone spectral projected gradient methods on convex set. SIAM J. Opt. 10, 1196–1211 (2000)

    Article  MATH  MathSciNet  Google Scholar 

  6. Birgin, E.G., Martinez, J.M., Raydan, M.: Algorithm 813: SPG-software for convex-constrained optimization. ACM Trans. Math. Softw. 27, 340–349 (2001)

    Article  MATH  Google Scholar 

  7. Birgin, E.G., Martinez, J.M., Raydan, M.: Spectral projected gradient methods. Encycl. Optim. 1, 3652–3659 (2009)

    Article  Google Scholar 

  8. Boyd, S., Mutapcic, A.: Subgradient methods. Notes for EE364b, Stanford University (2008)

  9. Caprara, A., Fischetti, M., Toth, P.: A heuristic method for the set covering problem. Oper. Res. 47, 730–743 (1999)

    Article  MATH  MathSciNet  Google Scholar 

  10. Crema, A., Loreto, M., Raydan, M.: Spectral projected subgradient with a momentum term for the lagrangean dual approach. Comput. Oper. Res. 34, 3174–3186 (2007)

    Article  MATH  MathSciNet  Google Scholar 

  11. La Cruz, W., Martinez, J.M., Raydan, M.: Spectral residual method without gradient information for solving large-scale nonlinear systems. Math. Comput. 75, 1449–1466 (2006)

    Article  Google Scholar 

  12. Geoffrion, A.M.: Lagrangean relaxation for integer programing. Math. Progr. Study 2, 82–114 (1974)

    Article  MathSciNet  Google Scholar 

  13. Goldstein, A.A.: Convex programming in Hilbert space. Bull. Am. Math. Soc. 70, 709–710 (1964)

    Article  MATH  Google Scholar 

  14. Grippo, L., Lampariello, F., Lucidi, S.: A nonmonotone line search technique for Newton’s method. SIAM J. Numer. Anal. 23, 707–716 (1986)

    Article  MATH  MathSciNet  Google Scholar 

  15. Held, M., Wolfe, P., Crowder, H.: Validation of subgradient optimization. Math. Progr. 6, 62–88 (1974)

    Article  MATH  MathSciNet  Google Scholar 

  16. Levitin, E.S., Polyak, B.T.: Constrained minimization problems. USSR Comput. Math. Math. Phys. 6, 1–50 (1966)

    Article  Google Scholar 

  17. Plaut, D., Nowlan, S., Hinton, G.E.: Experiments on learning by back propagation. Technical Report CMU- CS- 86-126, Department of Computer Science, Carnegie Mellon University, Pittsburgh, PA (1986)

  18. Polyak, B.T.: A general method of solving stremum problems. Sov. Math. Dokl. 8, 593–597 (1967)

    MATH  Google Scholar 

  19. Raydan, M.: On the Barzilai and Borwein choice of steplength for the gradient method. IMA J. Numer. Anal. 13, 321–326 (1993)

    Article  MATH  MathSciNet  Google Scholar 

  20. Raydan, M.: The Barzilai and Borwein gradient method for the large scale unconstrained minimization problem. SIAM J. Opt. 7, 26–33 (1997)

    Article  MATH  MathSciNet  Google Scholar 

  21. Shor, N.Z.: Minimization Methods for Non-differentiable Functions. Springer Series in Computational Mathematics. Springer, Berlin (1985)

    Book  MATH  Google Scholar 

Download references

Acknowledgments

The authors thank to José Mario Martínez for his constructive suggestions and to two anonymous referees whose comments helped us to improve the quality of this paper.

Author information

Authors and Affiliations

  1. School of Science, Technology, Engineering, and Mathematics (STEM), University of Washington Bothell, 18115 Campus Way NE, Bothell, WA, 90011-8246, USA

    Milagros Loreto

  2. Departamento de Computación, Facultad de Ciencias, Universidad Central de Venezuela, Ap. 47002, Caracas, 1041-A, Venezuela

    Alejandro Crema

Authors
  1. Milagros Loreto
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Alejandro Crema
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Milagros Loreto.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Loreto, M., Crema, A. Convergence analysis for the modified spectral projected subgradient method. Optim Lett 9, 915–929 (2015). https://doi.org/10.1007/s11590-014-0792-0

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11590-014-0792-0

Keywords