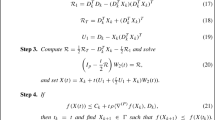Abstract
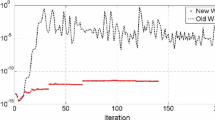
Newton’s method for unconstrained optimization problems on the Euclidean space can be generalized to that on Riemannian manifolds. The truncated singular value problem is one particular problem defined on the product of two Stiefel manifolds, and an algorithm of the Riemannian Newton’s method for this problem has been designed. However, this algorithm is not easy to implement in its original form because the Newton equation is expressed by a system of matrix equations which is difficult to solve directly. In the present paper, we propose an effective implementation of the Newton algorithm. A matrix-free Krylov subspace method is used to solve a symmetric linear system into which the Newton equation is rewritten. The presented approach can be used on other problems as well. Numerical experiments demonstrate that the proposed method is effective for the above optimization problem.




Similar content being viewed by others
References
Absil, P.-A., Mahony, R., Sepulchre, R.: Optimization Algorithms on Matrix Manifolds. Princeton University Press, Princeton (2008)
Edelman, A., Arias, T.A., Smith, S.T.: The geometry of algorithms with orthogonality constraints. SIAM J. Matrix Anal. Appl. 20, 303–353 (1998)
Eisenstat, S.C., Elman, H.C., Schultz, M.H.: Variational iterative methods for nonsymmetric systems of linear equations. SIAM J. Numer. Anal. 20, 345–357 (1983)
Golub, G.H., Van Loan, C.F.: Matrix Computations, 3rd edn. The Johns Hopkins University Press, Baltimore and London (1996)
Huang, W., Absil, P.-A., Gallivan, K.: Intrinsic representation of tangent vectors and vector transport on matrix manifolds. Universite Catholique de Louvain, Tech. report-UCL-INMA-2016.08 (2016)
Saad, Y.: Iterative Methods for Sparse Linear Systems, 2nd edn. SIAM, Philadelphia (2003)
Sato, H., Iwai, T.: A Riemannian optimization approach to the matrix singular value decomposition. SIAM J. Optim. 23, 188–212 (2013)
Acknowledgments
The authors would like to thank the reviewers for their careful reading and constructive comments. The present study was supported in part by JSPS KAKENHI Grant Numbers 15K17498 and 16K17647.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Aihara, K., Sato, H. A matrix-free implementation of Riemannian Newton’s method on the Stiefel manifold. Optim Lett 11, 1729–1741 (2017). https://doi.org/10.1007/s11590-016-1090-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11590-016-1090-9