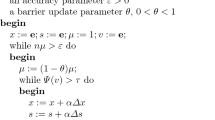Abstract
The introduction of kernel function in primal-dual interior point methods represents not only a measure of the distance between the iterate and the central path, but also plays an important role in the amelioration of the computational complexity of an interior point algorithm. In this work, we present a primal-dual interior point method for linear optimization problems based on a new kernel function with an efficient logarithmic barrier term. We derive the complexity bounds for large and small-update methods respectively. We obtain the best known complexity bound for large-update given by Peng et al., which improves significantly the so far obtained complexity results based on a logarithmic kernel function given by El Ghami et al. The results obtained in this paper are the first with respect to the kernel function with a logarithmic barrier term.

Similar content being viewed by others
References
Karmarkar, N.K.: A new polynomial-time algorithm for linear programming. In: Proceedings of the 16th Annual ACM Symposium on Theory of Computing, vol. 4, pp. 373–395 (1984)
Peng, J., Roos, C., Terlaky, T.: Self-Regularity: A New Paradigm for Primal-Dual Interior Point Algorithms. Princeton University Press, Princeton (2002)
Roos, C., Terlaky, T., Vial, J.P.: Theory and Algorithms for Linear Optimization, An Interior Point Approach. Wiley, Chichester (1997)
Ye, Y.: Interior Point Algorithms, Theory and Analysis. Wiley, Chichester (1997)
El Ghami, M.: New Primal-Dual Interior-Point Methods Based on Kernel Functions. PhD Thesis, TU Delft, The Netherlands (2005)
Peng, J., Roos, C., Terlaky, T.: A new and efficient large-update interior point method for linear optimization. J. Comput. Technol. 6, 61–80 (2001)
Bai, Y.Q., El Ghami, M., Roos, C.: A comparative study of kernel functions for primal-dual interior point algorithms in linear optimization. SIAM J. Optim. 15(1), 101–128 (2004)
El Ghami, M., Ivanov, I.D., Roos, C., Steihaug, T.: A polynomial-time algorithm for \(\text{ LO }\) based on generalized logarithmic barrier functions. Int. J. Appl. Math. 21, 99–115 (2008)
Bai, Y.Q., Lesaja, G., Roos, C., Wang, G.Q., El Ghami, M.: A class of large-update and small-update primal-dual interior-point algorithms for linear optimization. J. Optim. Theory Appl. 138, 341–359 (2008)
Bai, Y.Q., Roos, C.: A polynomial-time algorithm for linear optimization based on a new simple kernel function. Optim. Methods Softw. 18, 631–646 (2003)
El Ghami, M., Guennoun, Z.A., Bouali, S., Steihaug, T.: Interior point methods for linear optimization based on a kernel function with a trigonometric barrier term. J. Comput. Appl. Math. 236, 3613–3623 (2012)
Bouafia, M., Benterki, D., Yassine, A.: Complexity analysis of interior point methods for linear programming based on a parameterized kernel function. RAIRO Oper. Res. 50, 935–949 (2016)
Bouafia, M., Benterki, D., Yassine, A.: An efficient primal-dual interior point method for linear programming problems based on a new kernel function with a trigonometric barrier term. J. Optim. Theory Appl. 170, 528–545 (2016)
Peyghami, M.R., Hafshejani, S.F., Shirvani, L.: Complexity of interior point methods for linear optimization based on a new trigonometric kernel function. J. Comput. Appl. Math. 255, 74–85 (2014)
Peyghami, M.R., Hafshejani, S.F.: Complexity analysis of an interior point algorithm for linear optimization based on a new proximity function. Numer. Algoritm. 67, 33–48 (2014)
Cai, X.Z., Wang, G.Q., El Ghami, M., Yue, Y.J.: Complexity analysis of primal-dual interior-point methods for linear optimization based on a new parametric Kernel function with a trigonometric barrier term. Abstr. Appl. Anal., pages Art. ID 710158, 11, (2014)
Kheirfam, B., Moslem, M.: A polynomial-time algorithm for linear optimization based on a new kernel function with trigonometric barrier term. YUJOR 25(2), 233–250 (2015)
Li, X., Zhang, M.: Interior-point algorithm for linear optimization based on a new trigonometric kernel function. Oper. Res. Lett 43(5), 471–475 (2015)
Bai, Y. Q., Roos, C.: A primal-dual interior point method based on a new kernel function with linear growth rate. In: Proceedings of the 9th Australian Optimization Day, Perth, Australia (2002)
Megiddo, N.: Pathways to the optimal set in linear programming. In: Megiddo, N. (ed.) Progress in Mathematical Programming: Interior Point and Related Methods, pp. 131–158. Springer, New York (1989)
Sonnevend, G.: An “analytic center” for polyhedrons and new classes of global algorithms for linear (smooth, convex) programming. In: Prekopa, A., Szelezsan, J., Strazicky, B. (eds.) System Modelling and Optimization: Proceedings of the 12th IFIP-Conference, Budapest, Hungary, 1985, Lecture Notes in Control and Inform. Sci, vol. 84, pp. 866–876. Springer, Berlin (1986)
Acknowledgements
The authors are very grateful and would like to thank the anonymous referees for their suggestions and helpful comments which significantly improved the presentation of this paper.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Bouafia, M., Benterki, D. & Yassine, A. An efficient parameterized logarithmic kernel function for linear optimization. Optim Lett 12, 1079–1097 (2018). https://doi.org/10.1007/s11590-017-1170-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11590-017-1170-5