Ratcheting with a bliss level of consumption

Abstract

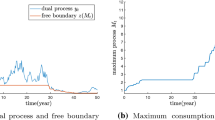
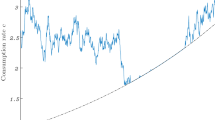
In this paper we study the portfolio selection problem of an agent who has a bliss point of consumption and does not tolerate a decline in consumption. We show that the optimal consumption process exhibits ratcheting and, as time elapses, the agent’s consumption approaches but never reaches the bliss level and her/his optimal investment in the risky asset approaches zero if the initial wealth level is not sufficient to maintain it. We use the martingale method and study the dual problem, which is similar to an incremental irreversible investment problem. We transform the dual problem into an optimal stopping problem, which has the same characteristic as finding the optimal exercise time of a perpetual American put option. We recover the value function by establishing a duality relationship and obtain a closed-form solution for the optimal consumption and portfolio strategy.

Appendix A derivation of the variational inequality (24)

We consider the optimal stopping problem

$$\begin{aligned} \begin{aligned} Q(y_t)=\max _{\tau \in \mathcal{S}_t}\mathbb {E}\left[ \left. e^{-\beta (\tau -t)}H(y_\tau )\right| \mathcal {F}_t \right] , \end{aligned}\end{aligned}$$

(36)

where $\mathcal{S}_t$ is the set of ${\mathcal {F}}$-stopping times $\tau \ge t$ and

$$\begin{aligned} H(z)=\dfrac{1}{\beta }-\dfrac{z}{r}. \end{aligned}$$

It is clear that

$$\begin{aligned} Q(y_t)\ge H(y_t). \end{aligned}$$

(37)

From the optimal stopping problem (36), for any $h>0$, the inclusion $\mathcal{S}_t\supset \mathcal{S}_{t+h}$ gives

$$\begin{aligned} \begin{aligned} e^{-\beta t}Q(y_t)=&\max _{\tau \in \mathcal {S}_t}\mathbb {E}\left[ \left. e^{-\beta \tau }H(y_{\tau })\right| \mathcal {F}_t\right] \\ =&\max _{\tau \in \mathcal {S}_t}\mathbb {E}\left[ \left. \mathbb {E}\left[ \left. e^{-\beta \tau } H(y_{\tau })\right| \mathcal {F}_{t+h}\right] \right| \mathcal {F}_t\right] \\ \ge&\mathbb {E}\left[ \left. \max _{\tau \in \mathcal {S}_{t+h}}\mathbb {E}\left[ \left. e^{-\beta \tau }H(y_\tau )\right| \mathcal {F}_{{t}+h}\right] \right| \mathcal {F}_t\right] \\ =&\mathbb {E}\left[ \left. e^{-\beta (t+h)}{Q}(y_{t+h})\right| \mathcal {F}_t\right] , \end{aligned} \end{aligned}$$

(38)

and the inequality (38) implies that $e^{-\beta t}Q(y_t)$ is a supermartingale under $\mathbb {P}$.

It follows that, by Itô’s Lemma

$$\begin{aligned} \dfrac{1}{2}\theta ^2y_t^2Q''(y_t) + (\beta -r)y_t Q'(y_t) - \beta Q(y_t) \le 0. \end{aligned}$$

(39)

When $Q(y_t) >H(y_t)$ which implies there exists $h>0$ small enough such that the optimal stopping time $\tau ^* \in \mathcal {S}_{t+h}$. Thus,

$$\begin{aligned} \begin{aligned} e^{-\beta t}Q(y_t)=&\,\max _{\tau \in \mathcal {S}_t}\mathbb {E}\left[ \left. e^{-\beta \tau }H(y_\tau )\right| \mathcal {F}_t\right] \\ =&\,\mathbb {E}\left[ \left. e^{-\beta \tau ^*}H(y_{\tau ^*}) \right| \mathcal {F}_t\right] \\ =&\,\mathbb {E}\left[ \left. {\max _{\tau \in \mathcal {S}_{t+h}}}\mathbb {E}\left[ \left. e^{-\beta \tau }H(y_\tau )\right| \mathcal {F}_{t+h}\right] \right| \mathcal {F}_t\right] \\ =&\,\mathbb {E}\left[ \left. e^{-\beta (t+h)}Q(y_{t+h})\right| \mathcal {F}_t\right] . \end{aligned} \end{aligned}$$

(40)

Hence, we can deduce that $e^{-\beta (\tau ^*\wedge t)}Q(y_{\tau ^*\wedge t})$ is a martingale under $\mathbb {P}$.

By applying Itô’s Lemma, we have

$$\begin{aligned} \dfrac{1}{2}\theta ^2y_t^2Q''(y_t) + (\beta -r)y_t Q'(y_t) - \beta Q(y_t) =0. \end{aligned}$$

(41)

Hence, (37), (39) and (41) imply that Q(z) satisfies

$$\begin{aligned} \begin{aligned} {\left\{ \begin{array}{ll} &{}Q(z)\ge H(z),\\ &{}\dfrac{1}{2}\theta ^2z^2Q''(z) + (\beta -r)z Q'(z) - \beta Q(z)\le 0,\\ &{}\left[ \dfrac{1}{2}\theta ^2z^2Q''(z) + (\beta -r)z Q'(z) - \beta Q(z)\right] \cdot [Q(z)-H(z)]=0. \end{array}\right. } \end{aligned} \end{aligned}$$

(42)