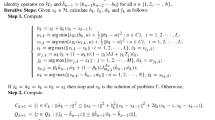Skip to main content
Springer Nature Link
Log in

Shrinking approximants for fixed point problem and generalized split null point problem in Hilbert spaces

  • Original Paper
  • Published:
Optimization Letters Aims and scope Submit manuscript

Abstract

This paper deals with the convergence analysis of a shrinking approximants for the computation of a common solution associated with the fixed point problem of \(\eta \)-demimetric operator and the generalized split null point problem in Hilbert spaces. The considered sequence of approximants is a variant of the parallel hybrid shrinking projection algorithm that converges strongly to the optimal common solution under suitable set of control conditions. The viability of the approximants with parallel implementation is demonstrated for various theoretical as well as numerical results. The results presented in this paper improve various existing results in the current literature.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

Availability of Data and Material

Data sharing not applicable to this article as no data-sets were generated or analysed during the current study.

References

  1. Agarwal, R.P., O’Regan, D., Sahu, D.R.: Fixed Point Theory for Lipschitzian-Type Mappings with Applications. Springer, New York (2009)

  2. Arfat, Y., Kumam, P., Ngiamsunthorn, P.S., Khan, M.A.A.: An inertial based forward–backward algorithm for monotone inclusion problems and split mixed equilibrium problems in Hilbert spaces. Adv. Differ. Equ. 2020, 453 (2020)

    Article  MathSciNet  Google Scholar 

  3. Arfat, Y., Kumam, P., Ngiamsunthorn, P.S., Khan, M.A.A., Sarwar, H., Din, H.F.: Approximation results for split equilibrium problems and fixed point problems of nonexpansive semigroup in Hilbert spaces. Adv. Differ. Equ. 2020, 512 (2020)

    Article  MathSciNet  Google Scholar 

  4. Arfat, Y., Kumam, P., Khan, M.A.A., Ngiamsunthorn, P.S., Kaewkhao, A.: An inertially constructed forward–backward splitting algorithm in Hilbert spaces. Adv. Differ. Equ. 2021, 124 (2021)

    Article  MathSciNet  Google Scholar 

  5. Arfat, Y., Kumam, P., Ngiamsunthorn, P.S., Khan, M.A.A.: An accelerated projection based parallel hybrid algorithm for fixed point and split null point problems in Hilbert spaces. Math. Methods Appl. Sci. (2021). https://doi.org/10.1002/mma.7405

    Article  Google Scholar 

  6. Bauschke, H.H., Matou\(\check{s}kov\acute{a}\), E., Reich, S.: Projection and proximal point methods: convergence results and counterexamples. Nonlinear Anal. 56, 715–738 (2004)

  7. Bauschke, H.H., Combettes, P.L.: Convex Analysis and Monotone Operator Theory in Hilbert Spaces, 2nd edn. Springer, Berlin (2017)

    Book  Google Scholar 

  8. Boyd, S., Ghaoui, L.E.I., Feron, E., Balakrishnan, V.: Linear matrix inequalities in system and control theory. SIAM Rev. 6, 66 (1995)

    MATH  Google Scholar 

  9. Browder, F.E., Petryshyn, W.V.: Construction of fixed points of nonlinear mappings in Hilbert spaces. J. Math. Anal. Appl. 20, 197–228 (1967)

    Article  MathSciNet  Google Scholar 

  10. Byrne, C.: A unified treatment of some iterative algorithms in signal processing and image reconstruction. Inverse Probl. 20(1), 103–120 (2004)

    Article  MathSciNet  Google Scholar 

  11. Censor, Y., Elfving, T.: A multiprojection algorithm using Bregman projections in a product space. Numer. Algorithms 8, 221–239 (1994)

    Article  MathSciNet  Google Scholar 

  12. Censor, Y., Elfving, T., Kopf, N., Bortfeld, T.: The multiple-sets split feasibility problem and its applications. Inverse Probl. 21, 2071–2084 (2005)

    Article  MathSciNet  Google Scholar 

  13. Censor, Y., Gibali, A., Reich, S.: Algorithms for the split variational inequality problem. Numer. Algorithms 59, 301–323 (2012)

    Article  MathSciNet  Google Scholar 

  14. Combettes, P.L.: The convex feasibility problem in image recovery. Adv. Imaging Electron Phys. 95, 155–453 (1996)

    Article  Google Scholar 

  15. Combettes, P.L., Pesquet, J.C.: Proximal splitting methods in signal processing. Fixed-Point Algorithms Inverse Prob. Sci. Eng. 66, 185–212 (2011)

    Article  MathSciNet  Google Scholar 

  16. Cui, H., Su, M.: On sufficient conditions ensuring the norm convergence of an iterative sequence to zeros of accretive operators. Appl. Math. Comput. 258, 67–71 (2015)

    MathSciNet  MATH  Google Scholar 

  17. Duchi, J., Shalev-Shwartz, S., Singer, Y., Chandra, T.: Efficient projections onto the l1-ball for learning in high dimensions. In: Proceedings of the 25th International Conference on Machine Learning, Helsinki, Finland (2008)

  18. Engl, H.W., Hanke, M., Neubauer, A.: Regularization of Inverse Problems. Kluwer, Dordrecht (2000)

    MATH  Google Scholar 

  19. Gibali, A., Küfer, K.H., Süss, P.: Successive linear programing approach for solving the nonlinear split feasibility problem. J. Nonlinear Convex A. 15(2), 345–353 (2014)

    MathSciNet  MATH  Google Scholar 

  20. Gibali, A.: A new split inverse problem and an application to least intensity feasible solutions. Pure Appl. Func. Anal. 2, 243–258 (2017)

    MathSciNet  MATH  Google Scholar 

  21. Gibali, A., Reich, S., Zalas, R.: Outer approximation methods for solving variational inequalities in Hilbert space. Optimization 66, 417–437 (2017)

    Article  MathSciNet  Google Scholar 

  22. Gibali, A., Sabach, S., Voldman, S.: Non-convex split feasibility problems: models, algorithms and theory. Open J. Math. Optim. 1, 1–15 (2020)

    Article  MathSciNet  Google Scholar 

  23. Goebel, K., Kirk, W.A.: Topics in Metric Fixed Point Theory, Cambridge Studies in Advanced Mathematics, vol. 28. Cambridge University Press, Cambridge (1990)

    Book  Google Scholar 

  24. Halpern, B.: Fixed points of nonexpansive maps. Bull. Am. Math. Soc. 73, 957–961 (1967)

    Article  Google Scholar 

  25. Herman, G.T.: Image Reconstruction from Projections: The Fundamentals of Computerized Tomography. Computer Science Applied Mathematics. Academic Press, New York (1980)

  26. Khan, M.A.A.: Convergence characteristics of a shrinking projection algorithm in the sense of Mosco for split equilibrium problem and fixed point problem in Hilbert spaces. Linear Nonlinear Anal. 3, 423–435 (2017)

    MathSciNet  MATH  Google Scholar 

  27. Khan, M.A.A., Arfat, Y., Butt, A.R.: A shrinking projection approach to solve split equilibrium problems and fixed point problems in Hilbert spaces. UPB. Sci. Bull. Ser. A 80(1), 33–46 (2018)

    MATH  Google Scholar 

  28. Phuangphoo, P., Kumam, P.: Two block hybrid projection method for solving a common solution for a system of generalized equilibrium problems and fixed point problems for two countable families. Optim. Lett. 7, 1745–1763 (2013)

    Article  MathSciNet  Google Scholar 

  29. Reich, S., Tuyen, T.M.: Iterative methods for solving the generalized split common null point problemin Hilbert spaces. Optimization 69, 1013–1038 (2019)

    Article  Google Scholar 

  30. Reich, S., Tuyen, T.M.: Parallel iterative methods for solving the generalized split common null point problem in Hilbert spaces. RACSAM 114, 180 (2020)

    Article  MathSciNet  Google Scholar 

  31. Takahashi, S., Takahashi, W.: The split common null point problem and the shrinking projection method in Banach spaces. Optimization 65, 281–287 (2016)

    Article  MathSciNet  Google Scholar 

  32. Takahashi, W.: The split common fixed point problem and the shrinking projection method in Banach spaces. J. Conv. Anal. 24, 1015–1028 (2017)

    MathSciNet  MATH  Google Scholar 

  33. Takahashi, W.: Strong convergence theorem for a finite family of demimetric mappings with variational inequality problems in a Hilbert space. Jpn. J. Ind. Appl. Math. 34, 41–57 (2017)

    Article  MathSciNet  Google Scholar 

  34. Takahashi, W.: Weak and strong convergence theorems for new demimetric mappings and the split common fixed point problem in Banach spaces. Numer. Funct. Anal. Optim. 39(10), 1011–1033 (2018)

    Article  MathSciNet  Google Scholar 

  35. Takahashi, W., Wen, C.F., Yao, J.C.: The shrinking projection method for a finite family of demimetric mappings with variational inequality problems in a Hilbert space. Fixed Point Theory 19, 407–419 (2018)

    Article  MathSciNet  Google Scholar 

  36. Vogel, C.R.: Computational Methods for Inverse Problems. SIAM, Philadelphia (2002)

    Book  Google Scholar 

Download references

Acknowledgements

The authors wish to thank the anonymous referees for their comments and suggestions. The authors (Y. Arfat, P. Kumam and P.S. Ngiamsunthorn) acknowledge the financial support provided by the Center of Excellence in Theoretical and Computational Science (TaCS-CoE), KMUTT. Moreover, this research project is supported by Thailand Science Research and Innovation (TSRI) Basic Research Fund: Fiscal year 2021 under project number 64A306000005. The author Yasir Arfat was supported by the Petchra Pra Jom Klao Ph.D Research Scholarship from King Mongkut’s University of Technology Thonburi, Thailand(Grant No.16/2562). Moreover, this project is funded by National Council of Thailand (NRCT) under Research Grants for Talented Mid-Career Researchers (Contract No. N41A640089).

Author information

Authors and Affiliations

  1. KMUTT Fixed Point Research Laboratory, KMUTT-Fixed Point Theory and Applications Research Group, Department of Mathematics, Faculty of Science, King Mongkut’s University of Technology Thonburi (KMUTT), 126 Pracha-Uthit Road, Bang Mod, Thung Khru, Bangkok, 10140, Thailand

    Yasir Arfat & Poom Kumam

  2. Center of Excellence in Theoretical and Computational Science (TaCS-CoE), SCL 802 Fixed Point Laboratory, Science Laboratory Building, King Mongkut’s University of Technology Thonburi (KMUTT), 126 Pracha-Uthit Road, Bang Mod, Thung Khru, Bangkok, 10140, Thailand

    Poom Kumam

  3. Research Center for Interneural Computing, China Medical University Hospital, China Medical University, Taichung, 40402, Taiwan

    Poom Kumam

  4. Department of Mathematics, COMSATS University Islamabad, Lahore Campus, Lahore, 54000, Pakistan

    Muhammad Aqeel Ahmad Khan

  5. Department of Mathematics, Faculty of Science, King Mongkut’s University of Technology Thonburi (KMUTT), 126 Pracha-Uthit Road, Bang Mod, Thung Khru, Bangkok, 10140, Thailand

    Parinya Sa Ngiamsunthorn

Authors
  1. Yasir Arfat
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Poom Kumam
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Muhammad Aqeel Ahmad Khan
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. Parinya Sa Ngiamsunthorn
    View author publications

    You can also search for this author inPubMed Google Scholar

Contributions

All authors contributed equally and significantly in writing this article. All authors read and approved the final manuscript.

Corresponding authors

Correspondence to Poom Kumam or Muhammad Aqeel Ahmad Khan.

Ethics declarations

Competing interests

The authors declare that they have no competing interests.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Arfat, Y., Kumam, P., Khan, M.A.A. et al. Shrinking approximants for fixed point problem and generalized split null point problem in Hilbert spaces. Optim Lett 16, 1895–1913 (2022). https://doi.org/10.1007/s11590-021-01810-4

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11590-021-01810-4

Keywords