A polynomial-time algorithm for a nonconvex chance-constrained program under the normal approximation

Abstract

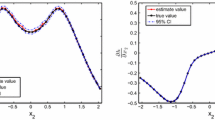
We study a chance-constrained optimization problem where the random variable appearing in the chance constraint follows a normal distribution whose mean and variance both depend linearly on the decision variables. Such structure may arise in many applications, including the normal approximation to the Poisson distribution. We present a polynomial-time algorithm to solve the resulting nonconvex optimization problem, and illustrate the efficacy of our method using a numerical experiment.

Appendices

Appendix A Solution to the single-edge subproblem

We now derive a solution for the single-edge subproblem (6), which is solved repeatedly in Algorithm 1. For the remainder of the section, we fix $i\in {N}$ and ${\hat{a}},{\hat{b}},{\hat{c}}\in {\mathbb {R}}$. We are interested in solving $\displaystyle \max _{\gamma \in [0,1]}\{c_i\gamma \mid {g(\gamma )\le 0}\}$ where

$$\begin{aligned} g(\gamma )=a_i\gamma +{\hat{a}}+\phi \sqrt{b_i\gamma +{\hat{b}}}-r. \end{aligned}$$

The function g is only defined for $\gamma \ge \gamma _0=-{\hat{b}}/b_i$, and is differentiable only for $\gamma >\gamma _0$, with derivative $g'(\gamma )=a_i+\tfrac{1}{2}\phi {b_i}/\sqrt{b_i\gamma +{\hat{b}}}$. From the form of the derivative, we see that if $a_i\ge 0$, the function g is monotonically increasing on its domain, and if $a_i<0$, g increases monotonically up to a point $\gamma _{\mathrm {max}}$, before decreasing monotonically as $\gamma \rightarrow \infty$. Hence, there are several cases, depending on whether $a_i\ge 0$ and $g(\gamma _0)>0$:

• Case 1 $a_i\ge 0$ and $g(\gamma _0)>0$. Then $g(\gamma )>0$ for all $\gamma \in [\gamma _0,\infty )$, and thus (6) is infeasible.

• Case 2 $a_i\ge 0$ and $g(\gamma _0)\le 0$. Then g has a single root $r_0$ that can be computed with the quadratic formula, and $g(\gamma )\le 0$ for all $\gamma \in [\gamma _0,r_0]$. If $r_0<0$, then (6) is infeasible. Otherwise $r_0\ge 0$, and the the optimal solution to (6) is

  $$\begin{aligned} \gamma ^*={\left\{ \begin{array}{ll} \min \{1,r_0\},&{}c_i>0,\\ 0,&{}{\text {otherwise}}. \end{array}\right. } \end{aligned}$$

• Case 3 $a_i<0$ and $g(\gamma _0)>0$. Then g has a single root $r_0$, and $g(\gamma )\le 0$ for all $\gamma \in [r_0,\infty )$. If $r_0>1$, then (6) is infeasible. Otherwise $r_0\le 1$, and the optimal solution is

  $$\begin{aligned} \gamma ^*={\left\{ \begin{array}{ll} 1,&{}c_i>0,\\ \max \{0,r_0\},&{}{\text {otherwise}}. \end{array}\right. } \end{aligned}$$

• Case 4 $a_i<0$ and $g(\gamma _0)\le 0$. In this case, the function g has a single local maximum at $\gamma _{\mathrm {max}}=-\big ({\hat{b}}-\tfrac{1}{4}(\phi {b_i}/a_i)^2\big )/b_i$.

  • Case 4a $g(\gamma _{\mathrm {max}})>0$. Then g has two roots $r_0$ and $r_1$, and $g(\gamma )\le 0$ for all $\gamma \in [\gamma _0,r_0]\cup [r_1,\infty )$. If $r_0<0<1<r_1$, then (6) is infeasible. If $c_i>0$, then

    $$\begin{aligned} \gamma ^*={\left\{ \begin{array}{ll} r_0,&{}r_0<1<r_1,\\ 1,&{}{\text {otherwise}}. \end{array}\right. } \end{aligned}$$

    Otherwise, if $c_i\le 0$, then

    $$\begin{aligned} \gamma ^*={\left\{ \begin{array}{ll} r_1,&{}r_0<0<r_1,\\ 0,&{}{\text {otherwise}}. \end{array}\right. } \end{aligned}$$

  • Case 4b $g(\gamma _{\mathrm {max}})\le 0$. Then $g(\gamma )\le 0$ for all $\gamma \ge \gamma _0$, and

    $$\begin{aligned} \gamma ^*={\left\{ \begin{array}{ll} 1,&{}c_i>0,\\ 0,&{}{\text {otherwise}}. \end{array}\right. } \end{aligned}$$

Appendix B Proof of Proposition 5

Lemma 13

Fix $y\in [0,{\bar{b}}]$ such that (5) is feasible, and let $\ell \in \{0,\dots ,L\}$ such that $y\in [y_\ell ,y_{\ell +1}]$. Then there exists an optimal solution $x^*$ for (5) such that $x_i^*=0$ for all $i\in N^0_\ell$ and $x_i^*=1$ for all $i\in {N^1_\ell }$.

Proof

Fix $y\in [0,{\bar{b}}]$ such that (5) is feasible, and let $\ell \in \{0,\dots ,L\}$ such that $y\in [y_\ell ,y_{\ell +1}]$. Let $x'$ be an optimal solution for (5). Suppose that $x'_i>0$ for some $i\in {N^0_\ell }$. The vector obtained by decreasing $x'_i$ to 0 (and leaving all other coordinates unchanged) is feasible, because $p_i(y)\ge 0$, and produces an objective value no worse than $x'$, because $c_i\le 0$. We conclude that this modified point is also optimal for (5). Repeating this argument for $i\in {N^0_\ell }$ such that $x'_i>0$, we obtain an optimal solution with ${\hat{x}}_i=0$ for all $i\in {N^0_\ell }$. Now suppose that ${\hat{x}}_i<1$ for some $i\in {N^1_\ell }$. If we increase ${\hat{x}}_i$ to 1, the resulting vector remains feasible (because $p_i(y)\le 0$) and produces an objective value no worse than ${\hat{x}}$ (because $c_i\ge 0$). Repeating this procedure for all $i\in {N^1_\ell }$ such that ${\hat{x}}_i=1$, we obtain a solution ${\tilde{x}}$ such that ${\tilde{x}}_i=0$ for all $i\in {N^0_\ell }$ and ${\tilde{x}}_i=1$ for all $i\in {N^1_\ell }$, as desired. $\square$

Now consider the following fractional knapsack problem, parameterized by $y\ge 0$,

$$\begin{aligned}&\max \;\sum _{i\in {N_\ell ^+\cup N_\ell ^-}}|c_i|v_i \end{aligned}$$

(B1a)

$$\begin{aligned}&{\mathrm {s.t.}}\;\sum _{i\in {N_\ell ^+\cup N_\ell ^-}}|p_i(y)|v_i\le r\sqrt{y}-\tfrac{1}{2}\phi y+\sum _{i\in N_\ell ^1\cup N_\ell ^-}|p_i(y)|\end{aligned}$$

(B1b)

$$\begin{aligned}&0\le v_i\le 1\;\forall \; i\in {N_\ell ^+}\cup N_\ell ^-, \end{aligned}$$

(B1c)

where $\ell \in \{0,\dots ,L\}$ such that $y\in [y_\ell ,y_{\ell +1}]$.

Lemma 14

Suppose that $v^*\in {\mathbb {R}}^{n_\ell }$ is optimal for (B1). Then the vector $x^*\in {\mathbb {R}}^n$ given by

$$\begin{aligned} x^*_i={\left\{ \begin{array}{ll} 1,&{}i\in {N^1_\ell },\\ 0,&{}i\in {N^0_\ell },\\ v^*_i,&{}i\in {N^+_\ell },\\ 1-v^*_i,&{}{\text {otherwise }}(i\in {N^-_\ell }) \end{array}\right. } \end{aligned}$$

is optimal for (5).

Proof

For brevity, in the proof, we drop the subscript $\ell$ on the index sets $N^+$, $N^-$, etc. Suppose that $v^*\in {\mathbb {R}}^{n_\ell }$ is optimal for (B1), and consider the optimization problem obtained from (B1) by replacing the variables $v_i$ for $i\in {N^-}$ with $1-v_i$:

$$\begin{aligned}&\max \;\sum _{i\in {N^+}}|{c_i}|{v_i}+\sum _{i\in {N^-}}|{c_i}|(1-v_i) \end{aligned}$$

(B2a)

$$\begin{aligned}&{\mathrm {s.t.}}\;\sum _{i\in {N^+}}|{p_i(y)}|{v_i}+\sum _{i\in {N^-}}|{p_i(y)}|(1-v_i)\le {r}\sqrt{y}-\tfrac{1}{2}\phi {y}+\sum _{i\in {N^1}\cup {N^-}}|{p_i(y)}|\end{aligned}$$

(B2b)

$$\begin{aligned}&0\le v_i\le 1\;\forall \;i\in {N^+\cup N^-} \end{aligned}$$

(B2c)

By applying the variable transformation $v_i\mapsto 1-v_i$ for $i\in {N^-}$, we have that the vector $v'\in {\mathbb {R}}^{n_\ell }$ given by

$$\begin{aligned} v'_i={\left\{ \begin{array}{ll} v^*_i,&{}i\in {N^+},\\ 1-v^*_i,&{}{\text {otherwise }}(i\in {N^-}), \end{array}\right. } \end{aligned}$$

is optimal for (B2). Next, using the fact that $c_i>0$, $p_i(y)\ge 0$ for all $i\in {N^+}$ and $c_i<0$, $p_i(y)\le 0$ for all $i\in {N^-}$, the problem (B2) can be equivalently expressed as

$$\begin{aligned}&\max \;\sum _{i\in {N^+}\cup {N^-}}c_iv_i \end{aligned}$$

(B3a)

$$\begin{aligned}&{\mathrm {s.t.}}\;\sum _{i\in {N^+}\cup {N^-}}p_i(y)v_i\le {r}\sqrt{y}-\tfrac{1}{2}\phi {y}+\sum _{i\in {N^1}}|p_i(y)|\end{aligned}$$

(B3b)

$$\begin{aligned}&0\le v_i\le 1\;\forall \;i\in {N^+\cup N^-} \end{aligned}$$

(B3c)

and thus $v'$ is optimal for (B3). The optimization problem (B3) may be equivalently expressed as

$$\begin{aligned}&\max \;\sum _{i\in {N}}c_iv_i \end{aligned}$$

(B4a)

$$\begin{aligned}&{\mathrm {s.t.}}\;\sum _{i\in N}p_i(y)v_i\le {r}\sqrt{y}-\tfrac{1}{2}\phi {y} \end{aligned}$$

(B4b)

$$\begin{aligned}&0\le v_i\le 1\;\forall \;i\in {N} \end{aligned}$$

(B4c)

$$\begin{aligned}&v_i=0\;\forall \;i\in {N^0} \end{aligned}$$

(B4d)

$$\begin{aligned}&v_1=1\;\forall \;i\in {N^1} \end{aligned}$$

(B4e)

and thus the vector $v''\in {\mathbb {R}}^n$ given by

$$\begin{aligned} v''_i={\left\{ \begin{array}{ll} 1,&{}i\in {N^1},\\ 0,&{}i\in {N^0},\\ v'_i=v^*_i,&{}i\in {N^+},\\ v'_i=1-v^*_i,&{}{\text {otherwise }}(i\in {N^-}), \end{array}\right. } \end{aligned}$$

is optimal for (B4). Note that (B4) is exactly (5), with the additional constraints (B4d) and (B4e). Consequently, the vector $v''$ is feasible for (5). We now show that $v''$ is optimal for (5). Suppose not. Then by Lemma 13, there exists ${\hat{v}}\in {\mathbb {R}}^n$ such that $c^\top {\hat{v}}>c^\top v''$ and ${\hat{v}}_i=0$ for all $i\in {N^0}$ and ${\hat{v}}_i=1$ for all $i\in {N^1}$. Hence, the vector ${\hat{v}}$ is feasible for (B4), and produces a strictly better objective value than $v''$. This contradicts the optimality of $v''$ for (B4), and we conclude that $v''$ is optimal for (5), as desired. $\square$

Note that, for all $i\in {N^+}\cup {N^-}$ and $y\not \in {Y^1}$, $p_i(y)/c_i>0$, and thus $|p_i(y)/c_i|=p_i(y)/c_i$. Lemma 15 follows immediately from the well-known greedy algorithm for fractional knapsack problems with strictly positive weight and cost coefficients, and its proof is omitted.

Lemma 15

For all $\ell \in \{0,\dots ,L\}$ and $y\in [y_\ell ,y_{\ell +1}]{\setminus} Y^1$, there exists $v^*\in {\mathbb {R}}^{n_\ell }$ and $k\in \{1,\dots ,n_\ell \}$ such that $v^*$ is optimal for (B1), and

$$\begin{aligned} v_i^*\in {\left\{ \begin{array}{ll} \{1\},&{}\pi _\ell ^{-1}(i)<k,\\ {[}0,1],&{}\pi _\ell ^{-1}(i)=k,\\ \{0\},&{}{\text {otherwise }}(\pi _\ell ^{-1}(i)>k). \end{array}\right. } \end{aligned}$$

(*)

Proof of Proposition 5

Fix $\ell \in \{0,\dots ,L\}$ and $y'\in [y_\ell ,y_{\ell +1}]{\setminus} {Y^1}$. By Lemma 15, there exists a vector $v^*\in {\mathbb {R}}^{n_\ell }$ and an index $k\in \{1,\dots ,n_\ell \}$ satisfying $(*)$ such that $v^*$ is optimal for (B1) with $y=y'$. Hence, by Lemma 14, the vector $x^*\in {\mathbb {R}}^n$ given by

$$\begin{aligned} x_i^*={\left\{ \begin{array}{ll} 1,&{}i\in {N_\ell ^1},\\ 0,&{}i\in {N_\ell ^0},\\ v_i^*,&{}i\in {N_\ell ^+},\\ 1-v_i^*,&{}{\text {otherwise }}(i\in {N_\ell ^-}) \end{array}\right. } \end{aligned}$$

is optimal for (5). To complete the proof, it suffices to show that $x^*\in {E^k_\ell }$. By construction, we have that $x^*_{\pi _\ell (k)}\in [0,1]$. Also, $x^*_i=0$ for all $i\in {N_\ell ^0}$, and $x^*_i=1$ for all $i\in {N_\ell ^1}$. If $i\in N_\ell ^+$ and $\pi _\ell ^{-1}(i)>k$, then $x^*_i=v_i^*=0$. If $i\in {N_\ell ^-}$ and $\pi _\ell ^{-1}(i)<k$, then $v_i^*=1$, so $x_i^*=1-v_i^*=0$. Similarly, if $i\in {N_\ell ^+}$ and $\pi _\ell ^{-1}(i)<k$, then $x_i^*=v_i^*=1$. Lastly, if $i\in {N_\ell ^-}$ and $\pi _\ell ^{-1}(i)>k$, then $v_i^*=0$, so $x_i^*=1-v_i^*=1$. We conclude that $x^*\in E^k_\ell$, as desired. $\square$