Skip to main content
Springer Nature Link
Log in

Numerical solution of delay fractional optimal control problems with free terminal time

  • Original Paper
  • Published:
Optimization Letters Aims and scope Submit manuscript

Abstract

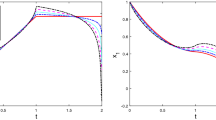
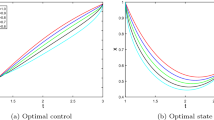
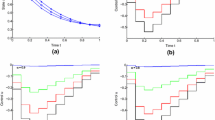
This paper considers a class of delay fractional optimal control problems with free terminal time. The fractional derivatives in this class of problems are described in the Caputo sense and they can be of different orders. We first show that for this class of problems, the well-known time-scaling transformation for mapping the free time horizon into a fixed time interval yields a new fractional-order system with variable time-delay. Then, we propose an explicit numerical scheme for solving the resulting fractional time-delay system, which gives rise to a discrete-time optimal control problem. Furthermore, we derive gradient formulas of the cost and constraint functions with respect to decision variables. On this basis, a gradient-based optimization approach is developed to solve the resulting discrete-time optimal control problem. Finally, an example problems is solved to demonstrate the effectiveness of our proposed solution approach.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2

Similar content being viewed by others

References

  1. Agrawal, O.: A general formulation and solution scheme for fractional optimal control problems. Nonlinear Dyn. 38, 323–337 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  2. Boccia, A., Falugi, P., Maurer, H., Vinter, R.B.: Free time optimal control problems with time delays. In: Proceedings of the 52nd IEEE CDC. pp. 520–525, Florence, Italy (2013)

  3. Caponetto, R., Dongola, G., Fortuna, L.: Fractional Order Systems: Modeling and Control Applications. World Scientific, London (2010)

    Book  MATH  Google Scholar 

  4. Chai, Q., Wang, W.: A computational method for free terminal time optimal control problem governed by nonlinear time delayed systems. Appl. Math. Model. 53, 242–250 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  5. Cong, N., Tuan, H.: Existence, uniqueness, and exponential boundedness of global solution to delay fractional differential equations. Mediter. J. Math. 14, 193 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  6. Debeljković, D.: Time-Delay Systems. InTech, Rijeka (2011)

    Book  Google Scholar 

  7. Gong, Z., Liu, C., Teo, K., Wang, S., Wu, Y.: Numerical solution of free final time fractional optimal control problems. Appl. Math. Comput. 405, 126270 (2021)

    MathSciNet  MATH  Google Scholar 

  8. Hosseinpour, S., Nazemi, A., Tohidi, E.: Müntz-Legendre spectral collocation method for solving delay fractional optimal control problems. J. Comput. Appl. Math. 351, 344–363 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  9. Hull, D.: Sufficient conditions for a minimum of the free-final-time optimal control problem. J. Optim. Theory Appl. 68, 275–286 (1991)

    Article  MathSciNet  MATH  Google Scholar 

  10. Kibass, A., Srivastava, A., Trujillo, I.: Theory and Application of Fractional Differential Equations. Elseveier, New York (2006)

    Google Scholar 

  11. Kumar, M.: Optimal design of fractional delay FIR filter using cuckoo search algorithm. Int. J. Circuit Theory Appl. 46, 2364–2379 (2018)

    Article  Google Scholar 

  12. Liu, C., Gong, Z., Teo, K., Sun, J., Caccetta, L.: Robust multi-objective optimal switching control arising in 1,3-propanediol microbial fed-batch process. Nonlinear Anal. Hybrid Syst. 25, 1–20 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  13. Liu, C., Gong, Z., Yu, C., Wang, S., Teo, K.: Optimal control computation for nonlinear fractional time-delay systems with state inequality constraints. J. Optim. Theory Appl. 191, 83–117 (2021)

    Article  MathSciNet  MATH  Google Scholar 

  14. Liu, C., Loxton, R., Teo, K.: A computational method for solving time-delay optimal control problems with free terminal time. Syst. Control Lett. 72, 53–60 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  15. Marzban, H., Malakoutikhah, F.: Solution of delay fractional optimal control problems using a hybrid of block-pulse functions and orthonormal Taylor polynomials. J. Frankl. Inst. 356, 8182–8251 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  16. Maurer, H.: Second order sufficient conditions for optimal control problems with free final time: the Ricati approach. SIAM J. Control Optim. 41, 380–403 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  17. Maurer, H., Osmolovskii, N.: Second order sufficient conditions for time-optimal bang-bang control. SIAM J. Control Optim. 42, 2239–2263 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  18. Monje, C., Chen, Y., Vinagre, B., Xue, D., Feliu, V.: Fractional-order Systems and Controls. Springer-Verlag, London (2010)

    Book  MATH  Google Scholar 

  19. Nocedal, J., Wright, S.J.: Numerical Optimization. Springer-Verlag, New York (2006)

    MATH  Google Scholar 

  20. Pooseh, S., Almeida, R., Torres, D.: Fractional order optimal control problems with free terminal time. J. Ind. Manag. Optim. 10, 363–381 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  21. Safaie, E., Farahi, M., Ardehaie, M.: An approximate method for numerically solving multi-dimensional delay fractional optimal control problems by Bernstein polynomials. Comput. Appl. Math. 34, 831–846 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  22. Salati, A., Shamsi, M., Torres, D.: Direct transcription methods based on fractional integral approximation formulas for solving nonlinear fractional optimal control problems. Commun. Nonlinear Sci. Numer. Simul. 67, 334–350 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  23. Sweilam, N., AL-Mekhlafi, S.: Optimal control for a time delay multi-strain tuberculosis fractional model: a numerical approach. IMA J. Math. Control Inform. 36, 317–340 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  24. Teo, K., Goh, C., Lim, C.: A computational method for a class of dynamical optimization problems in which the terminal time is conditionally free. IMA J. Math. Control Inform. 6, 81–95 (1989)

    Article  MathSciNet  MATH  Google Scholar 

  25. Teo, K., Li, B., Yu, C., Rehbock, V.: Applied and Computational Optimal Control: A Control Parametrization Approach. Springer, Cham (2021)

    Book  MATH  Google Scholar 

  26. Wang, Z., Hong, X., Shi, G.: Analysis of nonlinear dynamics and chaos in a fractional order financial system with time delay. Comput. Math. Appl. 62, 1531–1539 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  27. Yu, Y.: Optimal control of a nonlinear time-Delay system in batch fermentation process. Math. Probl. Eng. (2014). https://doi.org/10.1155/2014/478081

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

This work was supported by the National Natural Science Foundation of China (Nos. 12271307 and 11771008), the Australian Research Council (No. DP190103361), the China Scholarship Council (No. 201902575002), and the Natural Science Foundation of Shandong Province, China (Nos. ZR2017MA005 and ZR2019MA031).

Author information

Authors and Affiliations

  1. School of Mathematics and Information Science, Shandong Technology and Business University, Yantai, 264005, China

    Chongyang Liu & Zhaohua Gong

  2. School of Electrical Engineering, Computing, and Mathematical Sciences, Curtin University, Perth, 6845, Australia

    Chongyang Liu & Song Wang

  3. School of Mathematical Sciences, Sunway University, 47500, Kuala Lumpur, Malaysia

    Kok Lay Teo

  4. Coordinated Innovation Center for Computable Modeling in Management Science, Tianjin University of Finance and Economics, Tianjin, 300222, China

    Kok Lay Teo

Authors
  1. Chongyang Liu
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Zhaohua Gong
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Song Wang
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. Kok Lay Teo
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Chongyang Liu.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Liu, C., Gong, Z., Wang, S. et al. Numerical solution of delay fractional optimal control problems with free terminal time. Optim Lett 17, 1359–1378 (2023). https://doi.org/10.1007/s11590-022-01926-1

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11590-022-01926-1

Keywords