Skip to main content

Advertisement

Springer Nature Link
Log in

Crosscumulants based approaches for the structure identification of Volterra models

  • Published:
International Journal of Automation and Computing Aims and scope Submit manuscript

Abstract

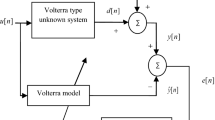
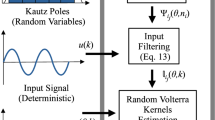
In this paper, we address the problem of structure identification of Volterra models. It consists in estimating the model order and the memory length of each kernel. Two methods based on input-output crosscumulants are developed. The first one uses zero mean independent and identically distributed Gaussian input, and the second one concerns a symmetric input sequence. Simulations are performed on six models having different orders and kernel memory lengths to demonstrate the advantages of the proposed methods.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Explore related subjects

Discover the latest articles and news from researchers in related subjects, suggested using machine learning.

References

  1. V. J. Mathews, G. L. Sicuranza. Polynomial Signal Processing, Wiley InterScience, 2000.

  2. T. Ogunfunmi. Adaptive Nonlinear System Identification: The Volterra and Wiener Model Approaches, Springer, 2007.

  3. O. M. Mohamed Vall, R. M’hiri. An Approach to Polynomial NARX/NARMAX Systems Identification in a Closed-loop with Variable Structure Control. International Journal of Automation and Computing, vol. 5, no. 3, pp. 313–318, 2005.

    Article  Google Scholar 

  4. S. A. Billings. Identification of Nonlinear Systems — A Survey. IEE Proceedings Part D: Control Theory and Applications, vol. 127, no. 6, pp. 272–285, 1980.

    Article  MathSciNet  Google Scholar 

  5. O. Nelles. Nonlinear System Identification, Springer, Berlin Heidelberg, Germany, 2001.

    MATH  Google Scholar 

  6. M. Schetzen. The Volterra and Wiener Theories of Nonlinear Systems, John Wiley and Sons Inc., New York, USA, 1980.

    MATH  Google Scholar 

  7. Y. Li, H. Kashiwagi. High-order Volterra Model Predictive Control and Its Application to a Nonlinear Polymerisation Process. International Journal of Automation and Computing, vol. 2, no. 2, pp. 208–214, 2005.

    Article  Google Scholar 

  8. P. Koukoulas, N. Kalouptsidis. Nonlinear System Identification Using Gaussian Inputs. IEEE Transactions on Signal Processing, vol. 43, no. 8, pp. 1831–1841, 1995.

    Article  MathSciNet  Google Scholar 

  9. P. Koukoulas, N. Kalouptsidis. Third order Volterra System Identification. In Proceedings of IEEE International Conference on Acoustics, Speech, and Signal Processing, IEEE Computer Society, vol. 3, pp. 2405–2408, 1997.

  10. P. Koukoulas, N. Kalouptsidis. Second-order Volterra System Identification. IEEE Transactions on Signal Processing, vol. 48, no. 12, pp. 3574–3577, 2000.

    Article  MATH  MathSciNet  Google Scholar 

  11. P. Koukoulas, N. Kalouptsidis. Blind Identification of Second Order Hammerstein Series. Signal Processing, vol. 83, no. 1, pp. 213–234, 2003.

    Article  MATH  Google Scholar 

  12. N. Kalouptsidis, P. Koukoulas. Blind Identification of Volterra — Hammerstein Systems. IEEE Transactions on Signal Processing, vol. 53, no. 8, pp. 2777–2787, 2005.

    Article  MathSciNet  Google Scholar 

  13. P. Koukoulas, V. Tsoulkas, N. Kalouptsidis. A Cumulant Based Algorithm for the Identification of Input-output Quadratic Systems. Automatica, vol. 38, no. 3, pp. 391–407, 2002.

    Article  MATH  MathSciNet  Google Scholar 

  14. E. J. Powers, C. P. Ritz, C.K. An, S.B. Kim, R.W. Miksad, S. W. Nam. Applications of Digital Polyspectral Analysis to Nonlinear Systems Modelling and Nonlinear Wave Phenomena. In Proceedings of Workshop on Higher-order Spectral Analysis, IEEE Press, Vail, Colorado, USA, pp. 73–77, 1989.

    Chapter  Google Scholar 

  15. J. M. Le Caillec, R. Garello. Time Series Nonlinearity Modelling: A Giannakis Formula Type Approach. Signal Processing, vol. 83, no. 8, pp. 1759–1788, 2003.

    Article  MATH  Google Scholar 

  16. G. H. Golub, C. F. Van Loan. Matrix Computations, The Johns Hopkins University Press, USA, 1996.

    MATH  Google Scholar 

  17. C. L. Nikias, A. P. Petropulu. Higher-order Spectra Analysis: A Nonlinear Signal Processing Framework, Prentice-Hall, Englewood Cliffs, New Jersey, USA, 1993.

    MATH  Google Scholar 

  18. J. L. Lacoume, P. O. Amblard, P. Comon. Statistiques d’ordre suprieur pour le traitement du signal, Masson, Paris, France, 1997. (in French)

    Google Scholar 

  19. J. M. Mendel. Tutorial on Higher Order Statistics (Spectra) in Signal Processing and System Theory: Theorical Results and Some Applications. Proceedings of the IEEE, vol. 79, no. 3, pp. 278–305, 1991.

    Article  Google Scholar 

  20. C. L. Nikias, J. M. Mendel. Signal Processing with Higher-order Spectra. IEEE Signal Processing Magazine, vol. 10, no. 3, pp. 10–37, 1993.

    Article  Google Scholar 

  21. G. Favier, Estimation paramètrique de modèles entresortie. In Signaux aléatoires: modélisation, estimation, détection, Traité IC2, chapitre 7, M. Gugliemi (ed.), Lavoisier, Hermes Science Publications, Paris, France, 2004. (in French)

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. National School of Engineers of Gabes, Route de Medenine, 6029, Gabes, Tunisia

    Houda Mathlouthi & Kamel Abederrahim

  2. National School of Engineers of Monastir, Avenue Ibn Jazzar, 5019, Monastir, Tunisia

    Faouzi Msahli

  3. I3S Laboratory, UNSA/CNRS, 2000 Route des Lucioles, Batiment Algorithmes Euclide, Sophia-Antipolis, Biot, France

    Gerard Favier

Authors
  1. Houda Mathlouthi
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Kamel Abederrahim
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Faouzi Msahli
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. Gerard Favier
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Houda Mathlouthi.

Additional information

Houda Mathlouthi received the engineering diploma in electrical engineering from the Ecole Nationale d’Ingenieurs de Gabes (ENIG), Tunisia in 2002, and the master degree in automatic control from the Ecole Nationale d’Ingenieurs de Sfax (ENIS), Tunisia. She is a member of Laboratory of Numerical Control of Industrial Processes (LACONPRI) at the ENIG from 2003. Currently, she is a Ph.D. candidate at the ENIS, and is an assistant at the ENIG.

Her research interests include linear and nonlinear process modeling and identification using higher-order statistics.

Kamel Abederrahim received the engineering diploma in electrical engineering from the Ecole Nationale d’Ingenieurs de Gabes (ENIG), Tunisia in 1992, and the master degree in automatic control from the Ecole Superieure des Sciences et Techniques de Tunis (ESSTT), Tunisia in 1995 and the Doctorate degree in electrical engineering from the Ecole Nationale d’Ingenieurs de Tunis (ENIT), Tunisia in 2000. He is a member of Laboratory of Numerical Control of Industrial Processes (LACONPRI) at the ENIG from 1995. He joined the ENIG as an assistant professor in 2000. From 2002 to 2005, he was the director of the Electrical Engineering Department at the ENIG, and now he is the director of the Institut Superieur des Systemes Industriels de Gabes (ISSIG), Tunisia.

His research interests include nonlinear process modeling, identification, and control.

Faouzi Msahli received the M. Sc. in electrical engineering from the Ecole Normale Suprieure de l’Enseignement Technique de Tunis (ENSET), Tunisia in 1987, and the Doctorate degree in electrical engineering from the Ecole Nationale d’Ingenieurs de Tunis (ENIT), Tunisia in 1996, and the Habilitation in electrical engineering from the Ecole Nationale d’Ingenieurs de Sfax (ENIS), Tunisia in 2002. He is a member of Laboratory of Numerical Control of Industrial Processes (LACONPRI) at the ENIG from 1988. He joined the ENIG as an assistant professor from 1989 to 1999, and now he works as a professor and an assistant director at the Ecole Nationale d’Ingenieurs de Monastir (ENIM), Tunisia.

His present research interests include nonlinear process modeling and identification, and predictive control.

Gerard Favier received the engineering diplomas from École Nationale Suprieure de Chronomtrie et de Micromcanique (ENSCM), Besanon, France and École Nationale Suprieure de l’Aronautique et de l’Espace (ENSAE), Toulouse, France and the engineering doctorate and state doctorate degrees from the University of Nice Sophia Antipolis, France in 1973, 1974, 1977, and 1981, respectively. In 1976, he joined the Centre National de la Recherche Scientifique (CNRS), France and now he works as a research director of CNRS at the I3S Laboratory, Sophia Antipolis. From 1995 to 1999, he was the director of the I3S Laboratory.

His research interests include nonlinear process modeling and identification, tensor modeling of wireless communication systems, nonlinear and blind equalization, and predictive control.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Mathlouthi, H., Abederrahim, K., Msahli, F. et al. Crosscumulants based approaches for the structure identification of Volterra models. Int. J. Autom. Comput. 6, 420–430 (2009). https://doi.org/10.1007/s11633-009-0420-0

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11633-009-0420-0

Keywords