1 Introduction

Complex dynamical networks (CDNs) are widespread in nature and human society, such as biological neural network, food web, Internet, world wide web, wireless communication network, power grid, citation network[1, 2]. Because of its broad background, CDN has attracted great interest of scientists in different fields. Since small world networks and scale-free networks were discovered, many interesting results have been got[3–15].

Synchronization is the basic property yet the most important one of CDN. It can be found everywhere, such as the phenomenon that fireflies glow at the same time, traffic jams, and network congestion. In the existing literature, there are many kinds of synchronization schemes for different needs. Dörfler and Bullo[3] explored different approaches to phase and frequency synchronization for complex oscillator networks. Cluster synchronization in a complex dynamical network with two-clusters was investigated in [4]. Also, Guo and Li[5] proposed asymptotic synchronization and synchronization in \(L_T^2\) norm, respectively.

In the real world, many networks are very large and it is almost impossible to get their global information. Distributed control scheme, for the absence of global information, has become more popular than centralized control scheme. Recently, distributed scheme have been widely concerned for synchronization of CDN[6–9]. In [6], the CDN with system delay and multiple coupling delays was studied via impulsive distributed control. The distributed consensus problem was considered in [7] for multi-agent systems with general continuous time linear dynamics. In [8], the filtering problem for sensor networks was investigated and a new type of distributed consensus filters was designed, where each sensor can communicate with the neighboring sensors, and filtering can be performed in a distributed way. General higher order distributed consensus protocols in multi-agent dynamical systems were studied in [9].

It is well-known that adaptive method can effectively deal CDN with unknown parameters. For example, synchronization of an uncertain dynamical network with time-varying delay was investigated by means of adaptive control schemes in [10]. Adaptive method combines naturally with distributed scheme for solving practical problems. An adaptive synchronization controller for distributed systems was presented in [11]. Yu et al.[12] designed an effective distributed adaptive strategy to tune the coupling weights of a network. An adaptive control strategy was developed in [13] for complex delayed dynamical networks with time-varying coupling strength and time-varying delays. By extending the result of [13], an adaptive synchronization was proposed for a class of nonlinearly parameterized complex dynamical networks with unknown time-varying parameters in [14]. Further, Shi et al.[15] designed the distributed adaptive learning laws of network with both periodically time-varying and constant parameters. This control scheme ensures synchronization no matter with or without derivative couplings. However, these results only considered the case of CDN with unknown time-varying coupling strength. The CDN with unknown time-varying coupling weights is not investigated yet.

Motivated by the above results, in this paper, we focus on the synchronization of a class of CDNs with unknown time-varying coupling weights. A distributed controller is proposed and edge-based adaptive update laws are designed to make the CDN achieve complete synchronization. Moreover, all the closed-loop signals are bounded.

The rest of the paper is organized as follows. The problem formulation and preliminaries are given in Section 2. In Section 3, the distributed controller and adaptive update laws are presented. Main results are displayed in Section 4. Simulation and conclusion are given in Section 5 and Section 6 respectively.

2 Formulation and preliminaries

Consider a dynamical network consisting of N identical nodes with unknown time-varying weights. Each node is an n dimensional dynamical system, and the state equation of the i-th node is

$$\matrix{{{{\dot x}_i} = f\left({{x_i}(t)} \right) +} \hfill \cr{\quad \quad \sum\limits_{j = 1,j \neq i}^N {{\eta _{ij}}(t){c_{ij}}\Gamma \left({{x_j}(t) - {x_i}(t)} \right),\quad i = 1,\;2,\; \cdots ,\;N}} \hfill \cr}$$
(1)

where x i = (x i 1, x i 2, ⋯,x in )T ∈ Rn represents the state vector of the i-th node, f: Rn → Rn is a smooth nonlinear vector-valued function, n ij (t) = a ij (t) + θ ij is the unknown time-varying weight, a ij (t) is an unknown time-varying continuous periodic function that with a known periodic T, and θ ij is unknown constant. a ij (t) > 0 if there exists a connection from node i to node j (j ≠ i), otherwise a ij (t) = 0. c ij is the coupling element, c ij = 1 if there exists a connection from node i to node j (j = i), otherwise c ij = 0. Γ = diag{γ1, γ2, ⋯,γ n } represents the inner coupling matrix with γ i > 0.

  • Definition 1. The network (1) is said to achieve asymptotic synchronization if

    $$\mathop {\lim}\limits_{t \rightarrow \infty} \left\Vert {{x_i}(t) - s(t)} \right\Vert = 0,\;i = 1,\;2,\; \cdots ,\;N$$
    (2)

    where ∥·∥ stands for the Euclidean vector norm. Let \(M = \{{[x_1^{\rm{T}},x_2^{\rm{T}} \cdots ,x_{\rm{N}}^{\rm{T}}]^{\rm{T}}}:{x_1}(t) = {x_2}(t) = \cdots = {x_N}(t) = s(t)\}\) be the synchronization manifold. s(t) satisfies s(t) = f(s(t)) and it can be an equilibrium point, periodic orbit, or even chaotic attractor.

  • Assumption 1. Suppose that there exists l i > 0, satisfying

    $$\matrix{{{{\left({{x_i}(t) - s(t)} \right)}^{\rm{T}}}\left({f({x_i}(t)) - f(s(t))} \right) \leq} \hfill \cr{\quad \quad \quad \quad \quad {l_i}{{\left({{x_i}(t) - s(t)} \right)}^{\rm{T}}}\left({{x_i}(t) - s(t)} \right)} \hfill \cr}$$
    (3)

    where x i (t) and s(t) are time varying vectors.

  • Lemma 1 (Young’s inequality). For any vectors x, y ∈ Rn, and any constant c > 0, the following matrix inequality holds:

    $${x^{\rm{T}}}y \leq c{x^{\rm{T}}}x + {{{y^{\rm{T}}}y} \over {4c}}.$$
    (4)

  • Lemma 2[16]. If e(t): [0, ∞) → R is square integrable, i.e., \({\lim _{t \to \infty}}\int_0^t {{e^2}(\tau){\rm{d}}\tau {\rm{<}}\infty}\), and ė(t) is bounded on [0, ∞), then limt→∞ e(t) = 0.

In this paper, a ij (t) is unknown periodic time-varying nonnegative parameters, the objective is to design a distributed adaptive controller under which the solutions of network (1) globally synchronize to s(t).

3 Distributed controller and adaptive update laws

In order to achieve the synchronization objective, we design a distributed adaptive controller for nodes in the network (1). Then, the controlled network is given by

$${\dot x_i}(t) = f\left({{x_i}(t)} \right) + \sum\limits_{j = 1,j \neq i}^N {{\eta _{ij}}(t){c_{ij}}\Gamma \left({{x_j}(t) - {x_i}(t)} \right) + {u_i}(t)}$$
(5)

where u i (t) = (u i 1(t), u i 2(t), ⋯, u in (t))T, i = 1, 2,⋯, N, are the distributed adaptive controllers to be designed.

A distributed controller is designed as

$$\matrix{{{u_i}(t) = - k\left({{x_i}(t) - s(t)} \right) +} \hfill \cr{\quad \quad \sum\limits_{j = 1,j \neq i}^N {{c_{ij}}\left({{{\hat a}_{ij}}(t) + {{\hat \theta}_{ij}}(t)} \right)\Gamma \left({{x_i}(t) - {x_j}(t)} \right)}} \hfill \cr}$$
(6)

where i = 1, 2, ⋯, N, a ij (t) and \({\hat \theta _{ij}}(t)\) are the estimation of a ij (t) and θ ij corresponding to those c ij = 1. In other word, we estimate those weights η ij (t) only when there exists a connection between nodes i and j (j ≠ i). â ij (t) and \({\hat \theta _{ij}}(t)\) satisfy the update laws as

$${\hat a_{ij}}(t) = \left\{{\matrix{{{{\hat a}_{ij}}(t - T) + {q_{ij}}{c_{ij}}e_i^{\rm{T}}(t)\Gamma \left({{e_j}(t) - {e_i}(t)} \right),} \hfill \cr{{\rm{if}}\quad t \in [T,\infty),\;j \neq i} \hfill \cr{{q_{ij0}}(t){c_{ij}}e_i^{\rm{T}}(t)\Gamma \left({{e_j}(t) - {e_i}(t)} \right),} \hfill \cr{{\rm{if}}\quad {{\rm{c}}_{ij}} = 1,\;t \in [0,T),\;j \neq i} \hfill \cr{0,\;{\rm{if}}\;t \in [ - T,0)} \hfill \cr}} \right.$$
(7)
$${\dot \hat \theta _{ij}} = {r_{ij}}{c_{ij}}e_i^{\rm{T}}(t)\Gamma \left({{e_j}(t) - {e_i}(t)} \right),\;j \neq i,\;{c_{ij}} = 1$$
(8)

where â ij (t) and \({\hat \theta _{ij}}(t)\) are the estimation of a ij (t) and θ ij . r ij and q ij are positive constants, q ij 0(t) are monotonically increasing functions on the interval [0, T] and satisfy q ij 0(T) = q ij .

The state error and the parameter estimation error are denoted by

$$\matrix{{{e_i}(t) = {x_i}(t) - s(t)} \hfill \cr{{{\tilde a}_{ij}}(t) = {a_{ij}}(t) - {{\hat a}_{ij}}(t)} \hfill \cr{{{\tilde \theta}_{ij}} = {\theta _{ij}} - {{\hat \theta}_{ij}}(t).} \hfill \cr}$$

. Then, we have the error system as

$$\matrix{{{{\dot e}_i}(t) = - {k_i}{e_i}(t) + f\left({{x_i}(t)} \right) - f\left({s(t)} \right) +} \hfill \cr{\quad \quad \sum\limits_{j = 1,j \neq i}^N {{c_{ij}}\left({{{\tilde a}_{ij}}(t) + {{\tilde \theta}_{ij}}(t)} \right)\Gamma \left({{e_j}(t) - {e_i}(t)} \right).}} \hfill \cr}$$
(9)

4 Main result

  • Theorem 1. Under Assumption 1, the distributed control law (6) with periodic adaptive law (7) and update law (8), guarantee the asymptotic synchronization of the controlled network (5), i.e.,

    $$\mathop {\lim}\limits_{t \rightarrow \infty} \Vert {{x_i}(t) - s(t)} \Vert = 0,\;i = 1,2, \cdots .N.$$
    (10)

    Moreover, all closed-loop signals are bounded.

  • Proof. We choose a Lyapunov-Krasovskii function as

    $$\matrix{{V(t) = {1 \over 2}\sum\limits_{i = 1}^N {e_i^{\rm{T}}(t){e_i}(t) + {1 \over 2}\sum\limits_{i = 1}^N {\sum\limits_{j = 1,j \neq i}^N {\int\limits_{t - T}^t {q_{ij}^{- 1}\tilde a_{ij}^2(\tau){\rm{d}}\tau {\rm{+}}}}}}} \hfill \cr{\quad \quad {1 \over 2}\sum\limits_{i = 1}^N {\sum\limits_{j = 1,j \neq i}^N {r_{ij}^{- 1}\tilde \theta _{ij}^2(t),\;t \in [0,\infty).}}} \hfill \cr}$$
    (11)

The proof process consists of two parts. Firstly, we prove the boundedness of V(t) on [0, T]. Secondly, the asymptotic synchronization will be achieved according to Lemma 2, and boundedness of all closed-loop signals will be proved.

At first, because â ij (t) has different expressions on [0, T] and [T, ∞), the proof procedure of the boundedness of V(t) is divided into two phases. When t ∈ [0, T], â ij (t) and \({\hat \theta _{ij}}(t)\) are continuous. From (6)–(8), one can obtain that the right-hand side of (9) is continuous. According to the existence theorem of solutions of differential equations, (9) has unique solution in interval [0, T1] ⊂ [0, T], with 0 < T1 ≤ T. Therefore, the boundedness of V(t) over [0, T1] can be guaranteed and we need only focus on the interval [T1, T).

The time derivative of V(t) on [T1, T] is given by

$$\matrix{{\dot V(t) = \sum\limits_{i = 1}^N {e_i^{\rm{T}}(t){{\dot e}_i}(t) + {1 \over 2}\sum\limits_{i = 1}^N {\sum\limits_{j = 1,j \neq i}^N {q_{ij}^{- 1} \times}}}} \hfill \cr{\quad \left({\tilde a_{ij}^2(t) - \tilde a_{ij}^2(t - T)} \right) - \sum\limits_{i = 1}^N {\sum\limits_{j = 1,j \neq i}^N {r_{ij}^{- 1}{{\tilde \theta}_{ij}}(t)}} \dot \hat \theta (t).} \hfill \cr}$$
(12)

Combining with (9) and Assumption 1, the first term on the right-hand side of (12) is

$$\matrix{{\sum\limits_{i = 1}^N {e_i^{\rm{T}}(t){{\dot e}_i}(t) =}} \hfill \cr{\quad \sum\limits_{i = 1}^N {e_i^{\rm{T}}(t)\left[ {f\left({{x_i}(t)} \right) - f\left({s(t)} \right) - {k_i}\left({{x_i}(t) - s(t)} \right)} \right] +}} \hfill \cr{\quad \sum\limits_{i = 1}^N {e_i^{\rm{T}}(t)\sum\limits_{j = 1,j \neq i}^N {{c_{ij}}\left({{{\tilde a}_{ij}}(t) + {{\tilde \theta}_{ij}}(t)} \right)\Gamma \left({{x_j}(t) - {x_i}(t)} \right) \leq}}} \hfill \cr{\quad \sum\limits_{i = 1}^N {({l_i} - {k_i})e_i^{\rm{T}}(t){e_i}(t) +}} \hfill \cr{\quad \sum\limits_{i = 1}^N {\sum\limits_{j = 1,j \neq i}^N {{c_{ij}}\left({{{\tilde a}_{ij}}(t) + {{\tilde \theta}_{ij}}(t)} \right)e_i^{\rm{T}}(t)\Gamma \left({{e_j}(t) - {e_i}(t)} \right) =}}} \hfill \cr{\quad \sum\limits_{i = 1}^N {({l_i} - {k_i})e_i^{\rm{T}}(t){e_i}(t) +}} \hfill \cr{\quad \sum\limits_{i = 1}^N {\sum\limits_{j = 1,j \neq i}^N {{c_{ij}}{{\tilde a}_{ij}}(t)e_i^{\rm{T}}(t)\Gamma \left({{e_j}(t) - {e_i}(t)} \right) +}}} \hfill \cr{\quad \sum\limits_{i = 1}^N {\sum\limits_{j = 1,j \neq i}^N {{c_{ij}}{{\tilde \theta}_{ij}}(t)e_i^{\rm{T}}(t)\Gamma \left({{e_j}(t) - {e_i}(t)} \right).}}} \hfill \cr}$$

By the periodic adaptive law (7), we have

$$\matrix{{\sum\limits_{i = 1}^N {e_i^{\rm{T}}(t){{\dot e}_i}(t) =}} \hfill \cr{\quad \sum\limits_{i = 1}^N {({l_i} - {k_i})e_i^{\rm{T}}(t){e_i}(t) + \sum\limits_{i = 1}^N {\sum\limits_{j = 1,j \neq i}^N {{{\tilde a}_{ij}}(t){{{{\hat a}_{ij}}(t)} \over {{q_{ij0}}(t)}}}} +}} \hfill \cr{\quad \sum\limits_{i = 1}^N {\sum\limits_{j = 1,j \neq i}^N {{c_{ij}}{{\tilde \theta}_{ij}}(t)e_i^{\rm{T}}(t)\Gamma \left({{e_j}(t) - {e_i}(t)} \right) =}}} \hfill \cr{\quad \sum\limits_{i = 1}^N {({l_i} - {k_i})e_i^{\rm{T}}(t){e_i}(t) +}} \hfill \cr{\quad \sum\limits_{i = 1}^N {\sum\limits_{j = 1,j \neq i}^N {{{\tilde a}_{ij}}(t){{{{\hat a}_{ij}}(t) - {a_{ij}}(t) + {a_{ij}}(t)} \over {{q_{ij0}}(t)}} +}}} \hfill \cr{\quad \sum\limits_{i = 1}^N {\sum\limits_{j = 1,j \neq i}^N {{c_{ij}}{{\tilde \theta}_{ij}}(t)e_i^{\rm{T}}(t)\Gamma \left({{e_j}(t) - {e_i}(t)} \right) =}}} \hfill \cr{\quad \sum\limits_{i = 1}^N {({l_i} - {k_i})e_i^{\rm{T}}(t){e_i}(t) - \sum\limits_{i = 1}^N {\sum\limits_{j = 1,j \neq i}^N {{{\tilde a_{ij}^2(t)} \over {{q_{ij0}}(t)}} +}}}} \hfill \cr{\quad \sum\limits_{i = 1}^N {\sum\limits_{j = 1,j \neq i}^N {{{{{\tilde a}_{ij}}(t){a_{ij}}(t)} \over {{q_{ij0}}(t)}} +}}} \hfill \cr{\quad \sum\limits_{i = 1}^N {\sum\limits_{j = 1,j \neq i}^N {{c_{ij}}{{\tilde \theta}_{ij}}(t)e_i^{\rm{T}}(t)\Gamma \left({{e_j}(t) - {e_i}(t)} \right).}}} \hfill \cr}$$

.

Then apply Lemma 1, for positive constant c and ε, ε is the lower bound of q ij 0(t) on interval [T1, T], we get

$$\matrix{{{{{{\tilde a}_{ij}}(t){a_{ij}}(t)} \over {{q_{ij}}(t)}} \leq {1 \over {{q_{ij0}}(t)}}[c\tilde a_{ij}^2(t) + {1 \over {4c}}a_{ij}^2(t)] \leq} \hfill \cr{\quad \;{c \over \varepsilon}\tilde a_{ij}^2(t) + {1 \over {4c\varepsilon}}a_{ij}^2(t)} \hfill \cr}$$

and

$$\matrix{{\sum\limits_{i = 1}^N {e_i^{\rm{T}}(t){{\dot e}_i}(t) \leq}} \hfill \cr{\quad \sum\limits_{i = 1}^N {({l_i} - {k_i})e_i^{\rm{T}}(t){e_i}(t) - \sum\limits_{i = 1}^N {\sum\limits_{j = 1,j \neq i}^N {{{\tilde a_{ij}^2(t)} \over {{q_{ij0}}(t)}} +}}}} \hfill \cr{\quad \sum\limits_{i = 1}^N {\sum\limits_{j = 1,j \neq i}^N {{c \over \varepsilon}\tilde a_{ij}^2(t) + \sum\limits_{i = 1}^N {\sum\limits_{j = 1,j \neq i}^N {{1 \over {4c\varepsilon}}a_{ij}^2(t) +}}}}} \hfill \cr{\quad \sum\limits_{i = 1}^N {\sum\limits_{j = 1,j \neq i}^N {{c_{ij}}{{\tilde \theta}_{ij}}(t)\Gamma \left({{e_j}(t) - {e_i}(t)} \right).}}} \hfill \cr}$$
(13)

By (12) and (13), we have

$$\matrix{{\dot V(t) \leq \sum\limits_{i = 1}^N {({l_i} - {k_i})e_i^{\rm{T}}(t){e_i}(t) - \sum\limits_{i = 1}^N {\sum\limits_{j = 1,j \neq i}^N {{{\tilde a_{ij}^2(t)} \over {{q_{ij0}}(t)}} +}}}} \hfill \cr{\quad \;\;\sum\limits_{i = 1}^N {\sum\limits_{j = 1,j \neq i}^N {{c \over \varepsilon}\tilde a_{ij}^2(t) + \sum\limits_{i = 1}^N {\sum\limits_{j = 1,j \neq i}^N {{1 \over {4c\varepsilon}}a_{ij}^2(t) +}}}}} \hfill \cr{\quad \;\sum\limits_{i = 1}^N {\sum\limits_{j = 1,j \neq i}^N {{c_{ij}}{{\tilde \theta}_{ij}}(t)e_i^{\rm{T}}(t)\Gamma \left({e_i^{\rm{T}}(t){e_i}(t)} \right) +}}} \hfill \cr{\quad \;{1 \over 2}\sum\limits_{i = 1}^N {\sum\limits_{j = 1,j \neq i}^N {q_{ij}^{- 1}\tilde a_{ij}^2(t) - \sum\limits_{i = 1}^N {\sum\limits_{j = 1,j \neq i}^N {r_{ij}^{- 1}{{\tilde \theta}_{ij}}(t){{\dot \hat \theta}_{ij}}(t).}}}}} \hfill \cr}$$

Substituting (8) into the above inequality, we have

$$\matrix{{\dot V(t) \leq \sum\limits_{i = 1}^N {({l_i} - {k_i})e_i^{\rm{T}}(t){e_i}(t) +}} \hfill \cr{\quad \;\;\sum\limits_{i = 1}^N {\sum\limits_{j = 1,j \neq i}^N {\left({{1 \over {2{q_{ij}}}} - {1 \over {{q_{ij0}}}}(t) + {c \over \varepsilon}} \right)\tilde a_{ij}^2(t) +}}} \hfill \cr{\quad \sum\limits_{i = 1}^N {\sum\limits_{j = 1,j \neq i}^N {{1 \over {4c\varepsilon}}a_{ij}^2(t).}} \;} \hfill \cr}$$
(14)

We chose k i and c such that \({l_i} - {k_i} < 0,{1 \over {2{q_{ij}}}} - {1 \over {{q_{ij}}_0}}(t) + {c \over \varepsilon} < 0\) for i, j = 1, 2,⋯, N, i ≠ j, then

$$\dot V(t) \leq \sum\limits_{i = 1}^N {\sum\limits_{j = 1,j \neq i}^N {{1 \over {4c\varepsilon}}a_{ij}^2(t).}}$$
(15)

As a ij (t) is continuous periodic function, we can see that a ij (t) is bounded. Therefore, \(\dot V(t)\) is bounded in [T1, T], and V(t) is bounded in interval [0, T].

When t ∈ [T, ∞], the derivative of V(t) is

$$\begin{array}{*{20}c} {\dot V(t) = \sum\limits_{i = 1}^N {e_i^T (t)\dot e_i (t) + } } \\ {\frac{1} {2}\sum\limits_{i = 1}^N {\sum\limits_{j = 1,j \ne 1}^N {\left[ {\tilde a_{ij}^2 (t) - \tilde a_{ij}^2 (t - T)} \right]q_{ij}^{ - 1} + } } } \\ {\sum\limits_{i = 1}^N {\sum\limits_{j = 1,j \ne i}^N {r_{ij}^{ - 1} \tilde \theta _{ij} (t)\dot \tilde \theta _{ij} (t) = } } } \\ {\sum\limits_{i = 1}^N {\left( {l_i - k_i } \right)e_i^T (t)e_i (t) + } } \\ {\sum\limits_{i = 1}^N {\sum\limits_{j = 1,j = 1}^N {c_{i\tilde jij} (t)e_i^T (t)\Gamma \left( {e_j (t) - e_i (t)} \right) + } } } \\ {\frac{1} {2}\sum\limits_{i = 1}^N {\sum\limits_{j = 1,j \ne 1}^N {\left[ {\tilde a_{ij}^2 (t) - \tilde a_{ij}^2 (t - T)} \right]q_{ij}^{ - 1} = } } } \\ {\sum\limits_{i = 1}^N {\left( {l_i - k_i } \right)e_i^T (t)e_i (t) + } } \\ {\sum\limits_{i = 1}^N {\sum\limits_{j = 1,j \ne 1}^N {c_{ij} \tilde a_{ij} (t)e_i^T (t)\Gamma \left( {e_j (t) - e_i (t)} \right) + } } } \\ {\frac{1} {2}\sum\limits_{i = 1}^N {\sum\limits_{j = 1,j \ne 1}^N {q_{ij}^{ - 1} \left( {\hat a_{ij} (t - T) - \hat a_{ij} (t)} \right)(2(a_{ij} (t) - } } } \\ {\hat a_{ij} (t)) + \hat a_{ij} (t) - \hat a_{ij} (t - T)) = } \\ {\sum\limits_{i = 1}^N {\left( {l_i - k_i } \right)e_i^T (t)e_i (t) + } } \\ {\sum\limits_{i = 1}^N {\sum\limits_{j = 1,j \ne 1}^N {c_{ij} \tilde a_{ij} (t)e_i^T (t)\Gamma \left( {e_j (t) - e_i (t)} \right) - } } } \\ {\sum\limits_{i = 1}^N {\sum\limits_{j = 1,j \ne 1}^N {c_{ij} \tilde a_{ij} (t)e_i^T (t)\Gamma \left( {e_j (t) - e_i (t)} \right) - } } } \\ {\frac{1} {2}\sum\limits_{i = 1}^N {\sum\limits_{j = 1,j \ne 1}^N {q_{ij}^{ - 1} \left( {\hat a_{ij} (t - T) - \hat a_{ij} (t)} \right)^2 = } } } \\ {\sum\limits_{i = 1}^N {\left( {l_i - k_i } \right)e_i^T (t)e_i (t) - } } \\ {\frac{1} {2}\sum\limits_{i = 1}^N {\sum\limits_{j = 1,j \ne 1}^N {q_{ij}^{ - 1} \left( {\hat a_{ij} (t - T) - \hat a_{ij} (t)} \right)^2 \leqslant } } } \\ {\sum\limits_{i = 1}^N {\left( {l_i - k_i } \right)e_i^T (t)e_i (t).} } \\ \end{array} $$
(16)

By the above equation, we have

$$V(t) - V(T) \leq \sum\limits_{i = 1}^N {\int\limits_T^t {({l_i} - {k_i})e_i^T(\tau){e_i}(\tau)d\tau \leq 0.}}$$
(17)

It can be derived naturally that V(t) ≤ V(T), i.e., V(t) is bounded in [T, ∞), so we get that V(t) is bounded in [0, ∞).

Secondly, we shall prove the asymptotical synchronization. For the sake of simplicity, the boundedness of all closed-loop signals is shown firstly, then the asymptotical synchronization is shown. By the boundedness of V(t), we can obtain that e i (t), ã ij (t) and \({\tilde \theta _{ij}}(t)\) are all bounded, and with the boundedness of a ij (t) and θ ij (t), we can see that â ij (t) and \({\hat \theta _{ij}}(t)\) are bounded too. Therefore, u i (t) and ė i (t) are bounded, respectively. By (17), we get \({\lim _{t \to \infty}}\int_0^t {e_i^{\rm{T}}(\tau){e_i}(\tau){\rm{d}}\tau {\rm{<}}\infty}\).

According to Lemma 2, we have limt→∞e i (t)=0, i = 1, 2,⋯, N, i.e., the controlled network (5) achieves asymptotic synchronization and all the closed-loop signals are bounded.

  • Remark 1. Generally speaking, the design of a distributed controller for network will use the coupling weights. That is why we use the adaptive method to estimate a ij (t).

  • Remark 2. Notice that the coupling matrix is not assumed to be symmetric or irreducible as compared to the assumptions in [9, 12], and the graph of network is not required to be connected. So our result is more general.

  • Remark 3. The control gain k i should be chosen as large as possible so that it can satisfy k i > l i to guarantee the boundedness of V(t). The initial states of nodes can be selected randomly from the whole Euclidean space noting that Assumption 1 is a globally Lipchitz condition.

  • Remark 4. In this paper, the distributed adaptive synchronization strategy can be seen as an edge-based version, which is different with the node-based one that has been discussed in many literatures[7, 13–15]. Authors in [7] proposed two distributed adaptive dynamic consensus protocols: One protocol assigns an adaptive coupling weight to each edge in the communication graph while the other uses an adaptive coupling strength for each node. Both of them guarantee consensus under the assumption that the communication graph G is connected, which can be omitted in our result. In [13], synchronization of complex delayed dynamical networks with time-varying coupling strength and time-varying delayed was investigated via adaptive control strategy. A new adaptive learning control approach is proposed for a class of nonlinearly parameterized complex dynamical networks with unknown time-varying parameters in [14]. Complex dynamical network model with both non-derivative and derivative couplings was considered in [15]. At the same time, the distributed adaptive learning laws of periodically time-varying parameters and constant parameters along with distributed adaptive control were designed. However, all the adaptive update laws in [13–15] are node-based and the synchronization in [14, 15] are both under \(L_T^2\) norm sense, while our adaptive update law is edge-based and we achieve an asymptotic synchronization.

5 Numerical simulation

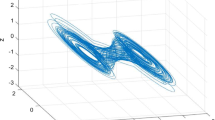
To demonstrate the theoretical result obtained in Section 4, the Chua’s chaotic circuit[14] is used as a dynamical node of the network.

Chua’s chaotic circuit is described by

$$\left\{{\matrix{{{{\dot x}_1} = p\left({- {x_1} + {x_2} - g({x_1})} \right)} \hfill \cr{{{\dot x}_2} = {x_1} + {x_2} + {x_3}} \hfill \cr{{{\dot x}_3} = - q{x_2}} \hfill \cr}} \right.$$
(18)

where \(g({x_1}) = {m_0}{x_1} + {1 \over 2}({m_1} - {m_0})(|{x_1} + 1| - |{x_1} - 1|),p = 10,q = 14.7,{m_0} = - 0.68\), p = 10, q = 14.7, m0 = −0.68, and m1 = −1.27.

The whole network is given by

$$\begin{array}{*{20}c} {\left( {\begin{array}{*{20}c} {\dot x_{i1} } \\ {\dot x_{i2} } \\ {\dot x_{i3} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {p\left( { - x_{i1} + x_{i2} - g\left( {x_{i1} } \right)} \right)} \\ {x_{i1} - x_{i2} + x_{i3} } \\ { - qx_{i2} } \\ \end{array} } \right) + \sum\limits_{j = 1,j \ne i}^N {\left( {a_{ij} \left( t \right) + \theta _{ij} } \right)c_{ij} \Gamma \left( {x_j \left( t \right) - x_i \left( t \right)} \right) + u_i \left( t \right),} } \\ {i = 1,2,3,4,5.} \\ \end{array} $$
(19)

The parameters are selected as

$$\matrix{{{r_{12}} = 0.4,\;{r_{14}} = 0.02,\;{r_{25}} = 0.5,\;{r_{35}} = 0.06,\;{r_{21}} = 0.1,} \hfill \cr{{r_{41}} = 0.2,\;{r_{52}} = 0.12,\;{r_{53}} = 0.32,\;{q_{12}} = 0.06,\;{q_{14}} = 0.08,} \hfill \cr{{q_{25}} = 0.09,\;{q_{35}} = 0.08,\;{q_{21}} = 0.06,\;{q_{41}} = 0.02,\;{q_{52}} = 0.04,} \hfill \cr{{q_{53}} = 0.06,\;{k_1} = {k_2} = {k_3} = {k_4} = {k_5} = 0.9,} \hfill \cr{{q_{ij0}}(t) = {{t{q_{ij}}} \over 6},\quad i = 1,2, \cdots ,5,\quad j = 1,2, \cdots ,5.} \hfill \cr}$$

The initial states are chosen as

$$\begin{array}{*{20}c} {x_1 (0) = (2,0, - 1)^T ,x_2 (0) = (3,1, - 2)^T } \\ {x_3 (0) = ( - 3, - 2,1)^T ,x_4 (0) = ( - 1,0, - 2)^T } \\ {x_5 (0) = ( - 1,1,0)^T ,s(0) = ( - 0.2,0.2,0.5)^T } \\ {C = \left( {\begin{array}{*{20}c} 0 & 1 & 0 & 1 & 0 \\ 1 & 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 & 1 \\ 1 & 0 & 0 & 0 & 0 \\ 0 & 1 & 1 & 0 & 0 \\ \end{array} } \right)} \\ {\Xi = \left( {\begin{array}{*{20}c} 0 & 3 & 0 & 2 & 0 \\ 3 & 0 & 0 & 0 & {0.7} \\ 0 & 0 & 0 & 0 & {1.2} \\ 2 & 0 & 0 & 0 & 0 \\ 0 & {0.7} & {1.2} & 0 & 0 \\ \end{array} } \right)} \\ {\Gamma = diag\{ 1,1,1\} } \\ {A_{12} (t) = \sin ^2 \left( {\frac{{2\pi t}} {6}} \right),A_{14} (t) = \left| {0.3\sin \left( {\frac{{2\pi t}} {3}} \right)} \right|} \\ {A_{21} (t) = \left| {\sin \left( {\frac{{2\pi t}} {6}} \right)} \right|,A_{25} (t) = \left( {0.7\cos \left( {\frac{{2\pi t}} {6}} \right)} \right)^2 } \\ {A_{35} (t) = \left| {\cos \left( {\frac{{2\pi t}} {3}} \right)} \right|,A_{41} (t) = \left( {0.3\sin \left( {\frac{{2\pi t}} {3}} \right)} \right)^2 } \\ {A_{52} (t) = \left| {0.7\cos \left( {\frac{{2\pi t}} {6}} \right)} \right|,A_{53} (t) = \cos ^2 \left( {\frac{{2\pi t}} {3}} \right).} \\ \end{array} $$

.

The first, second and third component of errors (inputs) are shown in the diagrams Fig. 1 (a) (Fig. 2 (a)), Fig. 1 (b) (Fig. 2 (b)) and Fig.1(c) (Fig. 2 (c)), respectively. From Fig. 1 we can see clearly that network (19) achieves asymptotic synchronization (for the sake of brevity, we only paste a part of figures here).

Fig. 1
figure 1

The evolution of error over time

Full size image
Fig. 2
figure 2

The response of control inputs

Full size image

Fig. 3 and Fig. 4 show that the estimations of both periodic parameters and constant parameters are bounded.

Fig. 3
figure 3

The evolution of estimation of periodic parameter

Full size image
Fig. 4
figure 4

The evolution of estimation of constant parameter

Full size image

6 Conclusions and Prospects

In this paper, we proposed a distributed adaptive control method to synchronize the complex dynamical network with unknown time-varying parameters. This method is applicable to more general cases, where the coupling matrix may be not symmetric or irreducible and the graph of network may be disconnected. To the best of our knowledge, both edge-based distributed adaptive synchronization strategy and node-based version are based on the known structure of topology of the complex dynamical network, the work about complex dynamical network with unknown structure of topology has not been reported as yet. It is an interesting and challenging problem about how to synchronize a network when its structure of topology cannot be achieved, and this is one problem for us to consider in the future.