Abstract
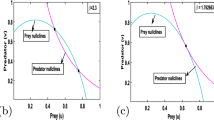
In this paper, effects of environmental and hunting parameters on the interspecific interacting populations are considered by applying the Rosenzweig-MacArthur model with the Holling type II functional response. Attenuating functions of the carrying capacity are introduced with a concern on the hunting parameters. We carry out numerical study to investigate how the population densities behave when environmental quantities change. We obtain the Hopf bifurcation diagrams from numerical results.
Similar content being viewed by others
Explore related subjects
Discover the latest articles and news from researchers in related subjects, suggested using machine learning.References
A. Hastings. Population Biology: Concepts and Models, New York, USA: Springer, 1998.
L. L. Rockwood. Introduction to Population Ecology, Malden, USA: Blackwell Publishing, 2006.
P. Turchin. Complex Population Dynamics: A Theoretical/Empirical Synthesis, Princeton, USA: Princeton University Press, 2003.
D. E. Huff, J. D. Varley. Natural regulation in Yellowstone National Park’s northern range. Ecological Applications, vol. 9, no. 1, pp. 17–29, 1999.
R. M. May. Stability and Complexity in Model Ecosystems, 2nd ed., Princeton, USA: Princeton University Press, 1975.
C. S. Holling. The functional response of invertebrate predators to prey density. Memoirs of the Entomological Society of Canada, vol. 98, no. S48, pp. 5–86, 1966.
M. L. Rosenzweig, R. H. MacArthur. Graphical representation and stability conditions of predator-prey interaction. American Naturalist, vol. 97, no. 895, pp. 209–223, 1963.
A. D. Bazykin. Nonlinear Dynamics of Interacting Populations, Singapore: World Scientific, 1998.
J. Hofbauer, K. Sigmund. Evolutionary Games and Population Dynamics, Cambridge, UK: Cambridge University Press, 1998.
J. D. Meiss. Differential Dynamical Systems, Philadelphia, USA: SIAM, 2007.
J. D. Murray. Mathematical Biology: I. An Introduction, 3rd ed., New York, USA: Springer, 2002.
J. D. Murray. Mathematical Biology: II. Spatial Models and Biomedical Applications, 3rd ed., New York, USA: Springer, 2003.
K. S. Cheng. Uniqueness of a limit cycle for a predator-prey system. SIAM Journal on Mathematical Analysis, vol. 12, no. 4, pp. 541–548, 1981.
Y. A. Kuznetsov. Elements of Applied Bifurcation Theory, 3rd ed., New York, USA: Springer-Verlag, 2004.
J. Sugie, Y. Saito. Uniqueness of limit cycles in a Rosenzweig-MacArthur model with prey immigration. SIAM Journal on Applied Mathematics, vol. 72, no. 1, pp. 299–316, 2012.
V. R. Alekseev, B. T. D. Stasio, J. J. Gilbert. Diapause in Aquatic Invertebrates: Theory and Human Use, Netherlands: Kluwer Academic Publishers, 2007.
M. Kuwamura, T. Nakazawa, T. Ogawa. A minimum model of prey-predator system with dormancy of predators and the paradox of enrichment. Journal of Mathematical Biology, vol. 58, no. 3, pp. 459–479, 2009.
M. Kuwamura, T. Nakazawa. Dormancy of predators dependent on the rate of variation in prey density. SIAM Journal on Applied Mathematics, vol. 71, no. 1, pp. 169–179, 2011.
Q. Fang, X. Y. Zhang. Effect of environment on preypredator systems with numerical simulation. In Proceedings of the 2014 International Conference on Life System Modeling and Simulation and 2014 International Conference on Intelligent Computing for Sustainable Energy and Environment: Communications in Computer and Information Science, Heidelberg, Germany: Springer, vol. 461, pp. 420–423, 2014.
Author information
Authors and Affiliations
Corresponding author
Additional information
This work was supported by National Natural Science Foundation of China (No. 11501032), and Scientific Research Grant-in-Aid from JSPS (No. 15K04987).
Recommended by Guest Editor Yang Song
Xiao-Yu Zhang received the B. Sc. degree in fundamental mathematics from Inner Mongolia University, China in 2005, the M. Sc. degree in fundamental mathematics from Fujian Normal University, China in 2009, and the Ph.D. degree in applied mathematics from Yamagata University, Japan in 2011. She is currently a lecture at Department of Mathematics, Beijing Forestry University. She is a member of MSJ and JSIAM.
Her research interests include complex analysis, numerical analysis, differential equations, dynamical systems, and mathematical modeling.
ORCID iD: 0000-0002-2794-3848
Qing Fang received the B. Sc. degree in fundamental mathematics from University of Science and Technology of China, China in 1985, the M. Sc. and Ph.D. degrees in applied mathematics from Hiroshima University, Japan in 1989 and 1992, respectively. He is currently a professor at Department of Mathematical Sciences, Yamagata University, Japan. He is a member of MSJ and JSIAM.
His research interests include numerical analysis, scientific computing, differential equations, dynamical systems and mathematical modeling.
Rights and permissions
About this article
Cite this article
Zhang, XY., Fang, Q. Numerical evaluation of external effects on interspecific interacting populations. Int. J. Autom. Comput. 13, 133–141 (2016). https://doi.org/10.1007/s11633-015-0938-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11633-015-0938-2