Abstract
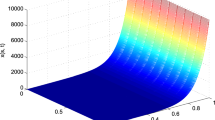
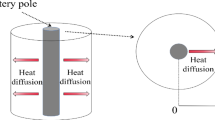
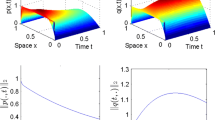
Boundary control for a class of partial integro-differential systems with space and time dependent coefficients is considered. A control law is derived via the partial differential equation (PDE) backstepping. The existence of kernel equations is proved. Exponential stability of the closed-loop system is achieved. Simulation results are presented through figures.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.References
J. Smoller. Shockwave and Reaction-diffusion Equations, Berlin, Germany: Springer-Verlag, pp. 12–24, 1994.
A. Smyshlyaev, M. Krstic. Explicit state and output feedback boundary controllers for partial differential equations. Journal of Automatic Control, vol. 13, no. 2, pp. 1–9, 2003.
A. Smyshlyaev, M. Krstic. Closed form boundary state feedbacks for a class of 1-D partial integro-differential equations. IEEE Transactions on Automatic Control, vol. 49, no. 12, pp. 2185–2202, 2004.
M. Krstic. Control of an unstable reaction-diffusion PDE with long input delay. System & Control Letters, vol. 58, no. 10–11, pp. 773–782, 2009.
M. Krstic, A. Smyshlyaev. Boundary Control of PDEs: A Course on Backstepping Designs, Philadelphia, USA: SIAM, pp. 29–50, 2008.
A. Smyshlyaev, M. Krstic. Adaptive Control of Parabolic PDEs, Princeton and Oxford, USA: Princeton University Press, pp. 30–60, 2010.
A. Smyshlyaev, M. Krstic. On control design for PDEs with space-dependent diffusivity or time-dependent reactivity. Automatica, vol. 41, no. 9, pp. 1601–1608, 2005.
T. Meurer, A. Kugi. Tracking control for boundary controlled parabolic PDEs with varying parameters: Combining backstepping and differential flatness. Automatica, vol. 45, no. 5, pp. 1182–1194, 2009.
B. Wang, J. Y. Zhai, S. M. Fei. Output feedback tracking control for a class of switched nonlinear systems with time-varying delay. International Journal of Automation and Computing, vol. 11, no. 6, pp. 605–612, 2014.
L. P. Liu, Z. M. Fu, X. N. Song. Tracking control of a class of differential inclusion systems via sliding mode technique. International Journal of Automation and Computing, vol. 11, no. 3, pp. 308–312, 2014.
Z. C. Zhou. Stabilization for boundary controlled cascaded heat-ODE system with time-dependent coefficient. In Proceedings of the 26th Chinese Control and Decision Conference, IEEE, Changsha, China, pp. 3744–3748, 2014.
X. Yu, C. Xu, J. Chu. Local exponential stabilization of Fisher’s equation using the backstepping technique. System & Control Letters, vol. 74, pp. 1–7, 2014.
K. Morton, D. Mayers. Numerical Solution of Partial Differential Equations, England: Post & Telecom Press, pp. 7–64, 2006.
D. Colton. Integral operators and reflection principles for parabolic equations in one space variable. Journal of Differential Equations, vol. 15, no. 3, pp. 551–559, 1974.
M. Krstic. Lyapunov stability of linear predictor feedback for time-varying input delay. IEEE Transactions on Automatic Control, vol. 55, no. 2, pp. 554–559, 2010.
Author information
Authors and Affiliations
Corresponding author
Additional information
Recommended by Associate Editor Zheng-Tao Ding
Yuan-Chao Si received the B. Sc. degree in mathematics and applied mathematics from University of Science and Technology Beijing, China in 2012, and received the M. Sc. degree in operational research and cybernetics from Southwest University, China in 2015.
His research interests include the boundary control of partial differential systems, nonlinear systems, coupled ordinary differential equation and partial differential equation systems.
Cheng-Kang Xie received the B. Sc. degree in mathematics from Southwest University, China, and received the M. Sc. degree in applied mathematics from Yunnan University, China, and received the Ph.D. degree in control engineering from University of Southampton, UK in 2004. He has published more than 50 papers on Systems & Control Letters, International Journal of Control, International Journal of Robust and Nonlinear Control, etc. He is with the School of Mathematics and System Science, Southwest University. He is the head of the Department of Applied Mathematics.
His research interests include distributed parametric systems, especially the boundary control of partial differential systems, and nonlinear systems.
Na Zhao received the B. Sc. degree in mathematics and applied mathematics from Shanxi Normal University, China in 2012, and now is a master student in cybernetics at Southwest University, China.
Her research interests include the boundary control of partial differential systems, coupled ordinary differential equation and partial differential equation systems.
Rights and permissions
About this article
Cite this article
Si, YC., Xie, CK. & Zhao, N. Boundary control for a class of reaction-diffusion systems. Int. J. Autom. Comput. 15, 94–102 (2018). https://doi.org/10.1007/s11633-016-1012-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11633-016-1012-4