Abstract
Cause-specific hazard models are a popular tool for the analysis of competing risks data. The classical modeling approach in discrete time consists of fitting parametric multinomial logit models. A drawback of this method is that the focus is on main effects only, and that higher order interactions are hard to handle. Moreover, the resulting models contain a large number of parameters, which may cause numerical problems when estimating coefficients. To overcome these problems, a tree-based model is proposed that extends the survival tree methodology developed previously for time-to-event models with one single type of event. The performance of the method, compared with several competitors, is investigated in simulations. The usefulness of the proposed approach is demonstrated by an analysis of age-related macular degeneration among elderly people that were monitored by annual study visits.








Similar content being viewed by others
References
Austin PC, Lee DS, Fine JP (2016) Introduction to the analysis of survival data in the presence of competing risks. Circulation 133:601–609
Berger M, Schmid M (2018) Semiparametric regression for discrete time-to-event data. Stat Model 18:1–24
Beyersmann J, Allignol A, Schumacher M (2011) Competing risks and multistate models with R. Springer, New York
Binder H, Allignol A, Schumacher M, Beyersmann J (2009) Boosting for high-dimensional time-to-event data with competing risks. Bioinformatics 25:890–896
Bou-Hamad I, Larocque D, Ben-Ameur H, Mâsse LC, Vitaro F, Tremblay RE (2009) Discrete-time survival trees. Can J Stat 37:17–32
Bou-Hamad I, Larocque D, Ben-Ameur H (2011) Discrete-time survival trees and forests with time-varying covariates: application to bankruptcy data. Stat Model 11:429–446
Breiman L (1996) Technical note: some properties of splitting criteria. Mach Learn 24:41–47
Breiman L, Friedman JH, Olshen RA, Stone JC (1984) Classification and regression trees. Wadsworth, Monterey
Cieslak DA, Chawla NV (2008) Learning decision trees for unbalanced data. In: Daelemans W, Goethals B, Morik K (eds) Machine learning and knowledge discovery in databases. Springer, Berlin, pp 241–256
Cieslak DA, Hoens TR, Chawla NV, Kegelmeyer WP (2012) Hellinger distance decision trees are robust and skew-insensitive. Data Min Knowl Discov 24:136–158
Cox DR (1972) Regression models and life-tables (with discussion). J R Stat Soc Series B 34:187–220
Doove LL, Dusseldorp E, Deun KV, Mechelen IV (2014) A comparison of five recursive partitioning methods to find person subgroups involved in meaningful treatment–subgroup interactions. Adv Data Anal Classif 8:403–425
Ferri C, Flach PA, Hernández-Orallo J (2003) Improving the AUC of probabilistic estimation trees. In: Lavrač N, Blockeel DGH, Todorovski L (eds) European conference on machine learning. Springer, Berlin, pp 121–132
Hastie T, Tibshirani R, Friedman J (2009) The elements of statistical learning, 2nd edn. Springer, New York
Hoens TR, Qian Q, Chawla NV, Zhou ZH (2012) Building decision trees for the multi-class imbalance problem. In: Tan P, Chawla S, Ho C, Bailey J (eds) Advances in knowledge discovery and data mining. Springer, Berlin, pp 122–134
Ibrahim NA, Kudus A, Daud I, Bakar MRA (2008) Decision tree for competing risks survival probability in breast cancer study. Int J Biol Med Sci 3:25–29
Ishwaran H, Gerds TA, Kogalur UB, Moore RD, Gange SJ, Lau BM (2014) Random survival forests for competing risks. Biostatistics 15:757–773
Janitza S, Tutz G (2015) Prediction models for time discrete competing risks. Ludwig-Maximilians-Universität München, Department of Statistics Technical Report, p 177
Lau B, Cole SR, Gange SJ (2009) Competing risk regression models for epidemiologic data. Am J Epidemiol 170:244–256
Luo S, Kong X, Nie T (2016) Spline based survival model for credit risk modeling. Eur J Oper Res 253:869–879
Meggiolaro S, Giraldo A, Clerici R (2017) A multilevel competing risks model for analysis of university students’ careers in italy. Stud High Educ 42:1259–1274
Mingers J (1989) An empirical comparison of pruning methods for decision tree induction. Mach Learn 4:227–243
Möst S, Pößnecker W, Tutz G (2016) Variable selection for discrete competing risks models. Qual Quant 50:1589–1610
Pößnecker W (2014) MRSP: multinomial response models with structured penalties. R package version 0.4.3. http://CRAN.R-project.org/package=MRSP
Prentice RL, Kalbfleisch JD, Peterson AV Jr, Flournoy N, Farewell VT, Breslow NE (1978) The analysis of failure times in the presence of competing risks. Biometrics 34:541–554
Provost F, Domingos P (2003) Tree induction for probability-based ranking. Mach Learn 52:199–215
Putter H, Fiocco M, Geskus RB (2007) Tutorial in biostatistics: competing risks and multi-state models. Stat Med 26:2389–2430
Quinlan JR (1986) Induction of decision trees. Mach Learn 1:81–106
Ripley BD (1996) Pattern recognition and neural networks. University Press, Cambridge
Schmid M, Küchenhoff H, Hörauf A, Tutz G (2016) A survival tree method for the analysis of discrete event times in clinical and epidemiological studies. Stat Med 35:734–751
Schmid M, Tutz G, Welchowski T (2018) Discrimination measures for discrete time-to-event predictions. Econ Stat 7:153–164
Steinberg JS, Göbel AP, Thiele S, Fleckenstein M, Holz FG, Schmitz-Valckenberg S (2016) Development of intraretinal cystoid lesions in eyes with intermediate age-related macular degeneration. Retina 36:1548–1556
Tapak L, Saidijam M, Sadeghifar M, Poorolajal J, Mahjub H (2015) Competing risks data analysis with high-dimensional covariates: an application in bladder cancer. Genomics Proteomics Bioinformatics 13:169–176
Tutz G (1995) Competing risks models in discrete time with nominal or ordinal categories of response. Qual Quant 29:405–420
Tutz G (2012) Regression for categorical data. University Press, Cambridge
Tutz G, Schmid M (2016) Modeling discrete time-to-event data. Springer, New York
Tutz G, Pößnecker W, Uhlmann L (2015) Variable selection in general multinomial logit models. Comput Stat Data Anal 82:207–222
Vallejos CA, Steel MFJ (2017) Bayesian survival modelling of university outcomes. J R Stat Soc Series A Stat Soc 180:613–631
Welchowski T, Schmid M (2017) discSurv: discrete time survival analysis. R package version 1.1.7. http://CRAN.R-project.org/package=discSurv
Xu W, Che J, Kong Q (2016) Recursive partitioning method on competing risk outcomes. Cancer Inform 15:CIN–S39364
Yee TW (2010) The VGAM package for categorical data analysis. J Stat Softw 32:1–34
Yee TW (2017) VGAM: vector generalized linear and additive models. R package version 1.0-4. https://CRAN.R-project.org/package=VGAM
Zahid FM, Tutz G (2013) Multinomial logit models with implicit variable selection. Adv Data Anal Classif 7:393–416
Acknowledgements
Support by the German Research Foundation (DFG), Grant SCHM 2966/1-2 and SCHM 2966/2-1, is gratefully acknowledged. The MODIAMD study is funded by the German Ministry of Education and Research (BMBF), Funding Number 13N10349.
Author information
Authors and Affiliations
Corresponding author
Appendix: Further simulation results
Appendix: Further simulation results
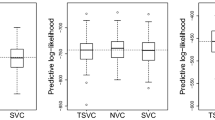
Results of the simulation study. The boxplots visualize the predictive log-likelihood values obtained from the various tree-based approaches for the six scenarios with \(n=500\). Dark gray boxplots refer to the results with splitting by Gini impurity (GI), light gray boxplots refer to the results with splitting by Hellinger distance (HD). High values of the predictive log-likelihood correspond to good model fits, and vice versa
Results of the simulation study. The boxplots visualize the predictive log-likelihood values obtained from various modeling approaches for the six scenarios with \(n=500\). The first two boxplots (GI and HD) obtained from the tree-based models refer to the results with tuning by the predictive log-likelihood (ll), respectively. The sixth boxplot in each of the six panels contains the true log-likelihood values of the 100 test data sets (True), based on the true hazards defined in (18). Dashed lines refer to the median values of the best-performing tree-based model
Rights and permissions
About this article
Cite this article
Berger, M., Welchowski, T., Schmitz-Valckenberg, S. et al. A classification tree approach for the modeling of competing risks in discrete time. Adv Data Anal Classif 13, 965–990 (2019). https://doi.org/10.1007/s11634-018-0345-y
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11634-018-0345-y
Keywords
- Discrete time-to-event data
- Competing risks
- Recursive partitioning
- Cause-specific hazards
- Regression modeling