Skip to main content

Advertisement

Springer Nature Link
Log in

Enhancing subspace clustering based on dynamic prediction

  • Research Article
  • Published:
Frontiers of Computer Science Aims and scope Submit manuscript

Abstract

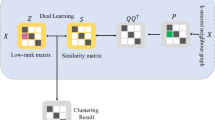
In high dimensional data, many dimensions are irrelevant to each other and clusters are usually hidden under noise. As an important extension of the traditional clustering, subspace clustering can be utilized to simultaneously cluster the high dimensional data into several subspaces and associate the low-dimensional subspaces with the corresponding points. In subspace clustering, it is a crucial step to construct an affinity matrix with block-diagonal form, in which the blocks correspond to different clusters. The distance-based methods and the representation-based methods are two major types of approaches for building an informative affinity matrix. In general, it is the difference between the density inside and outside the blocks that determines the efficiency and accuracy of the clustering. In this work, we introduce a well-known approach in statistic physics method, namely link prediction, to enhance subspace clustering by reinforcing the affinity matrix.More importantly,we introduce the idea to combine complex network theory with machine learning. By revealing the hidden links inside each block, we maximize the density of each block along the diagonal, while restrain the remaining non-blocks in the affinity matrix as sparse as possible. Our method has been shown to have a remarkably improved clustering accuracy comparing with the existing methods on well-known datasets.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Vidal R. Subspace clustering. IEEE Signal Processing Magazine, 2010, 28(2): 52–68

    Article  Google Scholar 

  2. Ng A Y, Jordan M I, Weiss Y. On spectral clustering: analysis and an algorithm. Advances in Neural Information Processing Systems, 2002, 2: 849–856

    Google Scholar 

  3. Von L U. A tutorial on spectral clustering. Statistics and Computing, 2007, 17(4): 395–416

    Article  MathSciNet  Google Scholar 

  4. Shi J, Malik J. Normalized cuts and image segmentation. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2000, 22(8): 888–905

    Article  Google Scholar 

  5. Costeira J, Kanade T. A multi-body factorization method for motion analysis. In: Proceedings of the 5th International Conference on Computer Vision. 1995, 1071–1076.

    Chapter  Google Scholar 

  6. Clauset A, Moore C, Newman M E J. Hierarchical structure and the prediction of missing links in networks. Nature, 2008, 453(7191): 98–101

    Article  Google Scholar 

  7. Lü L, Medo M, Yeung C H, Zhang Y C, Zhang Z K, Zhou T. Recommender systems. Physics Reports, 2012, 519(1): 1–49

    Article  Google Scholar 

  8. Liben-Nowell D, Kleinberg J. The link-prediction problem for social networks. Journal of the Association for Information Science and Technology, 2007 58(7): 1019–1031

    Google Scholar 

  9. Elhamifar E, Vidal R. Sparse subspace clustering. In: Proceeding of IEEE Conference on Computer Vision and Pattern Recognition. 2009, 2790–2797

    Google Scholar 

  10. Elhamifar E, Vidal R. Sparse subspace clustering: algorithm, theory, and applications. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2013, 35(11): 2765–2781

    Article  Google Scholar 

  11. Liu G, Lin Z, Yu Y. Robust subspace segmentation by low-rank representation. In: Proceedings of the 27th International Conference on Machine Learnin. 2010, 663–670

    Google Scholar 

  12. Liu G, Lin Z, Yan S, Sun J, Yu Y, Ma Y. Robust recovery of subspace structures by low-rank representation. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2013, 35(1): 171–184

    Article  Google Scholar 

  13. Wei S, Yu Y. Subspace segmentation with a minimal squared frobenius norm representation. In: Proceeding of International Conference on Pattern Recognition. 2012, 3509–3512

    Google Scholar 

  14. Zhang H, Yi Z, Peng X. fLRR: fast low-rank representation using Frobenius-norm. Electronics Letters, 2014, 5013: 936–938

    Article  Google Scholar 

  15. Michael G, Stephen B. CVX: Matlab software for disciplined convex programming, version 2.1, Recent Advances in Learning and Control, 2008

    Google Scholar 

  16. Michael G, Stephen B. Graph Implementations for Nonsmooth Convex Programs. Recent Advances in Learning and Control, London: Springer-Verlag Limited, 2008, 95–110

    Google Scholar 

  17. Liu J, Ji S, Ye J. SLEP: sparse learning with efficient projections. Arizona State University, 2009, 6(491): 7

    Google Scholar 

  18. Cai J F, Candès E J, Shen Z. A singular value thresholding algorithm for matrix completion. SIAM Journal on Optimization, 2010, 20(4): 1956–1982

    Article  MathSciNet  MATH  Google Scholar 

  19. Wright J, Ganesh A, Rao S, Peng Y, Ma Y. Robust principal component analysis: exact recovery of corrupted low-rank matrices via convex optimization. Advances in Neural Information Processing Systems, 2009, 2080–2088

    Google Scholar 

  20. Lin Z, Ganesh A, Wright J, Wu L, Chen M, Ma Y. Fast convex optimization algorithms for exact recovery of a corrupted low-rank matrix. Computational Advances in Multi-Sensor Adaptive Processing, 2009, 61(6): 1–18

    Google Scholar 

  21. Lin Z, Chen M, Ma Y. The augmented lagrange multiplier method for exact recovery of corrupted low-rank matrices. UIUC Technical Report UILU-ENG-09-2215, 2010

    Google Scholar 

  22. Carlson F D, Sobel E, Watson G S. Linear relationships between variables affected by errors. Biometrics, 1966, 252–267

    Google Scholar 

  23. Tikhonov A. Solution of incorrectly formulated problems and the regularization method. Soviet Math., 1963, 4: 1035–1038

    MATH  Google Scholar 

  24. Chen Y, Zhang L, Yi Z. A Novel low rank representation algorithm for subspace clustering. International Journal of Pattern Recognition and Artificial Intelligence, 2016, 30(4): 1650007

    Article  MathSciNet  Google Scholar 

  25. Feng J, Lin Z, Xu H, Yan S. Robust subspace segmentation with blockdiagonal prior. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. 2014, 3818–3825

    Google Scholar 

  26. Liu G, Yan S. Latent low-rank representation for subspace segmentation and feature extraction. In: Proceedings of the IEEE International Conference on Computer Vision. 2011, 1615–1622

    Google Scholar 

  27. Liu R, Lin Z, De la Torre F, Su Z. Fixed-rank representation for unsupervised visual learning. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. 2012, 598–605

    Google Scholar 

  28. Lü L, Zhou T. Link prediction in complex networks: a survey. Physica A: Statistical Mechanics and its Applications, 2011, 390(6): 1150–1170

    Article  Google Scholar 

  29. Casella G, Berger R L. Statistical Inference, Pacific Grove, CA: Duxbury, 2002.

    MATH  Google Scholar 

  30. Redner S. Networks: teasing out the missing links. Nature, 2008, 453(7191): 47–48

    Article  Google Scholar 

  31. Sales-Pardo M, Guimera R, Moreira A A, Amaral L A N. Extracting the hierarchical organization of complex systems. Proceedings of the National Academy of Sciences, 2007, 104(39): 15224–15229

    Article  Google Scholar 

  32. Getoor L, Friedman N, Koller D, Pfeffer A. Learning Probabilistic Relational Models. Relational Data Mining, Springer, Berlin, Hedelberg, 2001, 307–335

    Chapter  Google Scholar 

  33. Heckerman D, Chickering D M, Meek C, Rounthwaite R, Kadie C. Dependency networks for inference, collaborative filtering, and data visualization. Journal of Machine Learning Research, 2000, 1(Oct): 49–75

    MATH  Google Scholar 

  34. Taskar B, Abbeel P, Koller D. Discriminative probabilistic models for relational data. In: Proceedings of the 18th Conference on Uncertainty in Artificial Intelligence. 2002, 485–492

    Google Scholar 

  35. Leicht E A, Holme P, Newman M E J. Vertex similarity in networks. Physical Review E, 2006, 73(2): 026120

    Article  Google Scholar 

  36. Ravasz E, Somera A L, Mongru D A, Oltvai Z N, Barabási A L. Hierarchical organization of modularity in metabolic networks. Science, 2002, 297(5586): 1551–1555

    Article  Google Scholar 

  37. Sørensen T. A method of establishing groups of equal amplitude in plant sociology based on similarity of species and its application to analyses of the vegetation on Danish commons. Biologiske Skrifter, 2984, 5: 1–34

    Google Scholar 

  38. Zhou T, Lü L, Zhang Y C. Predicting missing links via local information. The European Physical Journal B-Condensed Matter and Complex Systems, 2009, 71(4): 623–630

    Article  MATH  Google Scholar 

  39. Pech R, Hao D, Pan L, Cheng H, Zhou T. Link prediction via matrix completion. EPL (Europhysics Letters), 2017, 117(3): 38002

    Article  Google Scholar 

  40. Jeh G, Widom J. SimRank: a measure of structural-context similarity. In: Proceedings of the 8th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. 2002, 538–543

    Google Scholar 

  41. Katz L. A new status index derived from sociometric analysis. Psychometrika, 1953, 18(1): 39–43

    Article  MATH  Google Scholar 

  42. Liu W, Lü L. Link prediction based on local random walk. EPL (Europhysics Letters), 2010, 89(5): 58007

    Article  Google Scholar 

  43. Lü L, Jin C H, Zhou T. Similarity index based on local paths for link prediction of complex networks, Physical Review E, 2009, 80(4): 046122

    Article  Google Scholar 

  44. Newman M E J. Clustering and preferential attachment in growing networks. Physical Review E, 2001, 64(2): 025102

    Article  Google Scholar 

  45. Murata T, Moriyasu S. Link prediction of social networks based on weighted proximity measures. In: Proceedings of the IEEE/WIC/ACM International Conference on Web Intelligence. 2007, 85–88

    Chapter  Google Scholar 

  46. Peng X, Zhang L, Yi Z. Constructing l2-graph for subspace learning and segmentation. 2012, arXiv preprint arXiv:1209.0841

    Google Scholar 

  47. Zheng X, Cai D, He X, Ma W Y, Lin X. Locality preserving clustering for image database. In: Proceedings of the 12th Annual ACM International Conference on Multimedia. 2004, 885–891

    Chapter  Google Scholar 

  48. Lee K C, Ho J, Kriegman D J. Acquiring linear subspaces for face recognition under variable lighting. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2005, 27(5): 684–698

    Article  Google Scholar 

  49. Hull J J. A database for handwritten text recognition research. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1994, 16(5): 550–554

    Article  Google Scholar 

  50. Street W N, Wolberg W H, Mangasarian O L. Nuclear feature extraction for breast tumor diagnosis. In: Proceedings of International Society for Optics and Photonics on Biomedical Image Processing and Biomedical Visualization. 1993, 861–870

    Chapter  Google Scholar 

  51. Siebert J P. Vehicle recognition using rule based methods. Project Report, 1987

    Google Scholar 

  52. Madeo R C B, Lima C A M, Peres S M. Gesture unit segmentation using support vector machines: segmenting gestures from rest positions. In: Proceedings of the 28th Annual ACM Symposium on Applied Computing. 2013, 46–52

    Google Scholar 

  53. Zhao Y, Karypis G. Criterion functions for document clustering: experiments and analysis. Citeseer: Technical Report, 2001

    MATH  Google Scholar 

  54. Cai D, He X, Han J. Document clustering using locality preserving indexing. IEEE Transactions on Knowledge and Data Engineering, 2005, 17(12): 1624–1637

    Article  Google Scholar 

Download references

Acknowledgements

The authors would like to thank the anonymous reviewers for the constructive comments and suggestions. This work was partially supported by the National Natural Science Foundation of China (Grant Nos. 61433014 and 71601029).

Author information

Authors and Affiliations

  1. Complex Lab, University of Electronic Science and Technology of China, Chengdu, 611731, China

    Ratha Pech, Dong Hao & Tao Zhou

  2. Big Data Research Center, University of Electronic Science and Technology of China, Chengdu, 611731, China

    Ratha Pech, Dong Hao & Tao Zhou

  3. Center for Robotics, University of Electronic Science and Technology of China, Chengdu, 611731, China

    Hong Cheng

Authors
  1. Ratha Pech
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Dong Hao
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Hong Cheng
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. Tao Zhou
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Tao Zhou.

Additional information

Ratha Pech received his MS degree in computer science from Sichuan University, China in 2013. He is currently working on his PhD in computer science in Complex Lab at University of Electronic Science and Technology of China. His research interests include graph mining, link prediction, and machine learning.

Dong Hao is an associate professor of Computer Science and Engineering at University of Electronic Science and Technology of China. He obtained his PhD in School of Informatics, Kyushu University, Japan. His research interests are topics in artificial intelligence, algorithmic game theory and social and economic networks. He mainly focus on reinforcement learning, games with Imperfect information, control in dynamic games and algorithmic mechanism design.

Hong Cheng is a full professor of University of Electronic Science and Technology of China, school of Automation and Engineering. He serves as an executive director of the Center for Robotics since 2014. He was a visiting scholar at School of Computer Science, Carnegie Mellon University, USA from 2006 to 2009. He received his PhD degree in Pattern Recognition and Intelligent Systems from Xi’an Jiaotong University in 2003 and became an associate Professor of Xi’an Jiaotong University since 2005. He joined UESTC since 2010. His current research interests include machine learning in human robot hybrid systems. He has over 100 academic publications including three books - Digital Signal Processing (Tsinghua University Press, Sep. 2007), Autonomous Intelligent Vehicles: Theory, Algorithms and Implementation (Springer, Dec. He served/is serving as a General Chair of VALSE 2015, Program Chair of CCPR 2016, and a General Chair for CCSR 2016). Now, he is a senior member of IEEE.

Tao Zhou is a full professor of University of Electronic Science and Technology of China. He is the director of Big Data Research Center. His research interests include big data, statistical physics, complex network, data science, sociology, economics, and human mobility. He has published more than 200 SCI papers, which are cited more than 10 000 times, H index more than 50.

Electronic supplementary material

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Pech, R., Hao, D., Cheng, H. et al. Enhancing subspace clustering based on dynamic prediction. Front. Comput. Sci. 13, 802–812 (2019). https://doi.org/10.1007/s11704-018-7128-7

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11704-018-7128-7

Keywords