Skip to main content
SpringerLink
Log in

Ordinal factorization machine with hierarchical sparsity

  • Research Article
  • Published:
Frontiers of Computer Science Aims and scope Submit manuscript

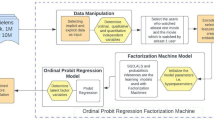
Abstract

Ordinal regression (OR) or classification is a machine learning paradigm for ordinal labels. To date, there have been a variety of methods proposed including kernel based and neural network based methods with significant performance. However, existing OR methods rarely consider latent structures of given data, particularly the interaction among covariates, thus losing interpretability to some extent. To compensate this, in this paper, we present a new OR method: ordinal factorization machine with hierarchical sparsity (OFMHS), which combines factorization machine and hierarchical sparsity together to explore the hierarchical structure behind the input variables. For the sake of optimization, we formulate OFMHS as a convex optimization problem and solve it by adopting the efficient alternating directions method of multipliers (ADMM) algorithm. Experimental results on synthetic and real datasets demonstrate the superiority of our method in both performance and significant variable selection.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Liu T Y. Learning to rank for information retrieval. Foundations and Trends in Information Retrieval, 2009, 3(3): 225–331

    Article  Google Scholar 

  2. Lee S K, Cho Y H, Kim S H. Collaborative filtering with ordinal scalebased implicit ratings for mobile music recommendations. Information Sciences, 2010, 180(11): 2142–2155

    Article  Google Scholar 

  3. Kim M, Pavlovic V. Structured output ordinal regression for dynamic facial emotion intensity prediction. In: Proceedings of European Conference on Computer Vision. 2010, 649–662

    Google Scholar 

  4. Rudovic O, Pavlovic V, Pantic M. Multi-output laplacian dynamic ordinal regression for facial expression recognition and intensity estimation. In: Proceedings of the the 2012 IEEE Conference on Computer Vision and Pattern Recognition. 2012, 2634–2641

    Chapter  Google Scholar 

  5. Kramer S, Widmer G, Pfahringer B, De Groeve M. Prediction of ordinal classes using regression trees. Fundamenta Informaticae, 2001, 14(1–2): 1–13

    MathSciNet  MATH  Google Scholar 

  6. Kotsiantis S, Pintelas P. A cost sensitive technique for ordinal classification problems. In: Proceedings of the Hellenic Conference on Artificial Intelligence. 2004, 220–229

    Google Scholar 

  7. Lin H T, Li L. Reduction from cost-sensitive ordinal ranking to weighted binary classification. Neural Computation, 2012, 24(5): 1329–1367

    Article  MATH  Google Scholar 

  8. Waegeman W, Boullart L. An ensemble of weighted support vector machines for ordinal regression. Transactions on Engineering, Computing and Technology, 2006, 12(3): 71–75

    Google Scholar 

  9. Chang K Y, Chen C S, Hung Y P. Ordinal hyperplanes ranker with cost sensitivities for age estimation. In: Proceedings of the 2011 IEEE Conference on Computer Vision and Pattern Recognition. 2011, 585–592

    Google Scholar 

  10. Chu W, Keerthi S. Support vector ordinal regression. Neural Computation, 2007, 19(3): 792–815

    Article  MathSciNet  MATH  Google Scholar 

  11. Sun B Y, Li J, Wu Dash D, Zhang X M, Li W B. Kernel discriminant learning for ordinal regression. IEEE Transactions on Knowledge and Data Engineering, 2010, 22(6): 906–910

    Article  Google Scholar 

  12. Chu W, Ghahramani Z. Gaussian processes for ordinal regression. Journal of Machine Learning Research, 2005, 6(7): 1019–1041

    MathSciNet  MATH  Google Scholar 

  13. Duda R, Hart P, Stork D. Pattern Classification. John Wiley & Sons, 2012

    Google Scholar 

  14. Rendle S. Factorization machines. In: Proceedings of the 10th International Conference on Data Mining. 2010, 995–1000

    Google Scholar 

  15. Yamada M, Lian W, Goyal A, Chen J, Wimalawarne K, Khan S, Kaski S, Mamitsuka H, Chang Y. Convex factorization machine for regression. 2015, arXiv preprint arXiv:1507.01073

    Google Scholar 

  16. Blondel M, Fujino A, Ueda N. Convex factorization machines. In: Proceedings of the Joint European Conference on Machine Learning and Knowledge Discovery in Databases. 2015, 19–35

    Chapter  Google Scholar 

  17. Fukunaga K. Introduction to Statistical Pattern Recognition. Elsevier, 2013

    Google Scholar 

  18. Bien J, Taylor J, Tibshirani R. A lasso for hierarchical interactions. Annals of Statistics, 2012, 41(3): 1111–1141

    Article  MathSciNet  MATH  Google Scholar 

  19. Yan X, Bien J. Hierarchical sparse modeling: a choice of two regularizers. 2015, arXiv preprint arXiv:1512.01631

    Google Scholar 

  20. Yuan M, Joseph V R, Zou H. Structured variable selection and estimation. The Annals of Applied Statistics, 2009, 3(4): 1738–1757

    Article  MathSciNet  MATH  Google Scholar 

  21. Haris A, Witten D, Simon N. Convex modeling of interactions with strong heredity. Journal of Computational and Graphical Statistics, 2016, 25(4): 981–1004

    Article  MathSciNet  Google Scholar 

  22. Zhao P, Rocha G, Yu B. The composite absolute penalties family for grouped and hierarchical variable selection. Annals of Statistics, 2009, 37(6A): 3468–3497

    Article  MathSciNet  MATH  Google Scholar 

  23. Radchenko P, James G M. Variable selection using adaptive nonlinear interaction structures in high dimensions. Journal of the American Statistical Association, 2011, 105(492): 1541–1553

    Article  MathSciNet  MATH  Google Scholar 

  24. Boyd S, Parikh N, Chu E, Peleato B, Eckstein J. Distributed optimization and statistical learning via the alternating direction method of multipliers. Foundations and Trends® in Machine Learning, 2011, 3(1): 1–122

    Article  MATH  Google Scholar 

  25. Blondel M, Fujino A, Ueda N, Ishihata M. Higher-order factorization machines. In: Proceedings of the 30th International Conference on Neural Information Processing Systems, 2016, 3359–3368

    Google Scholar 

  26. Blondel M, Ishihata M, Fujino A, Ueda N. Polynomial networks and factorization machines: new insights and efficient training algorithms. In: Proceedings of the International Conference on Machine Learning. 2016, 850–858

    Google Scholar 

  27. Jacob L, Obozinski G, Vert J P. Group lasso with overlap and graph lasso. In: Proceedings of the 26th International Conference on Machine Learning. 2009, 433–440

    Google Scholar 

  28. She Y, Wang Z, Jiang H. Group regularized estimation under structural hierarchy. Journal of the American Statistical Association, 2018, 113(521): 445–454

    Article  MathSciNet  MATH  Google Scholar 

  29. Lim M, Hastie T. Learning interactions via hierarchical group-lasso regularization. Journal of Computational and Graphical Statistics, 2015, 24(3): 627–654

    Article  MathSciNet  Google Scholar 

  30. Bach F, Jenatton R, Mairal J, Obozinski G. Structured sparsity through convex optimization. Statistical Science, 2012, 27(4): 450–468

    Article  MathSciNet  MATH  Google Scholar 

  31. Beck A, Teboulle M. A fast iterative shrinkage-thresholding algorithm for linear inverse problems. SIAM Journal on Imaging Sciences, 2009, 2(1): 183–202

    Article  MathSciNet  MATH  Google Scholar 

  32. Lu C, Zhu C, Xu C, Yan S, Lin Z. Generalized singular value thresholding. In: Proceedings of the 29th AAAI Conference on Artificial Intelligence. 2015, 1805–1811

    Google Scholar 

  33. Cai J F, Candès E J, Shen Z. A singular value thresholding algorithm for matrix completion. SIAM Journal on Optimization, 2010, 20(4): 1956–1982

    Article  MathSciNet  MATH  Google Scholar 

  34. Gutierrez P, Perezortiz M, Sanchezmonedero J, Fernandeznavarro F, Hervasmartinez C. Ordinal regression methods: survey and experimental study. IEEE Transactions on Knowledge and Data Engineering, 2016, 28(1): 127–146

    Article  Google Scholar 

  35. Xu B, Bu J, Chen C, Cai D. An exploration of improving collaborative recommender systems via user-item subgroups. In: Proceedings of the International Conference on World Wide Web. 2012, 21–30

    Google Scholar 

  36. Rendle S. Factorization machines with libFM. ACM Transactions on Intelligent Systems and Technology (TIST), 2012, 3(3): 57

    Google Scholar 

  37. Rhee S Y, Taylor J, Wadhera G, Benhur A, Brutlag D L, Shafer R W. Genotypic predictors of human immunodeficiency virus type 1 drug resistance. Proceedings of the National Academy of Sciences, 2006, 103(46): 17355–17360

    Article  Google Scholar 

  38. Kang Z, Peng C, Cheng Q. Robust PCA via nonconvex rank approximation. In: Proceedings of the International Conference on Data Mining (ICDM). 2015, 211–220

    Google Scholar 

Download references

Acknowledgements

This work was partially supported by the National Natural Science Foundation of China (Grant Nos. 61472186, 61702273) and the Natural Science Foundation of Jiangsu Province (BK20170956).

Author information

Authors and Affiliations

  1. College of Computer Science and Technology, Nanjing University of Aeronautics and Astronautics, Nanjing, 210000, China

    Shaocheng Guo & Songcan Chen

  2. School of Computer and Software, Nanjing University of Information Science and Technology, Nanjing, 210044, China

    Qing Tian

Authors
  1. Shaocheng Guo
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Songcan Chen
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Qing Tian
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Songcan Chen.

Additional information

Shaocheng Guo received his BS degree and master degree in computer science from Nanjing University of Aeronautics & Astronautics (NUAA), China in 2015 and 2018, respectively. His research interest is machine learning.

Songcan Chen received the BS degree from Hangzhou University (now merged into Zhejiang University), the MS degree from Shanghai Jiao Tong University and the PhD degree from Nanjing University of Aeronautics and Astronautics (NUAA), China in 1983, 1985, and 1997, respectively. He joined in NUAA in 1986, and since 1998, he has been a full-time professor with the Department of Computer Science and Engineering. He has authored/co-authored over 170 scientific peer-reviewed papers and ever obtained Honorable Mentions of 2006, 2007 and 2010 Best Paper Awards of Pattern Recognition Journal, respectively. His current research interests include pattern recognition, machine learning, and neural computing.

Qing Tian received his PhD degree in computer science from Nanjing University of Aeronautics and Astronautics, China in 2016. He is currently an assistant professor in the School of Computer and Software, Nanjing University of Information Science and Technology, China and is currently visiting, as an academic visitor, at the University of Manchester, UK. He is the recipient of the ICPR Best Scientific Paper Awardin 2016, the Excellent Doctoral Disser-tation Award of Jiangsu Province of China in 2017, etc. His research interests include machine learning and pattern recognition, especially in the areas of ordinal regression and metric learning and its applications.

Electronic supplementary material

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Guo, S., Chen, S. & Tian, Q. Ordinal factorization machine with hierarchical sparsity. Front. Comput. Sci. 14, 67–83 (2020). https://doi.org/10.1007/s11704-019-7290-6

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11704-019-7290-6

Keywords

Search

Navigation