Abstract
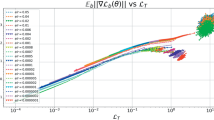
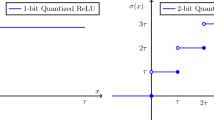
Deep learning performs as a powerful paradigm in many real-world applications; however, its mechanism remains much of a mystery. To gain insights about nonlinear hierarchical deep networks, we theoretically describe the coupled nonlinear learning dynamic of the two-layer neural network with quadratic activations, extending existing results from the linear case. The quadratic activation, although rarely used in practice, shares convexity with the widely used ReLU activation, thus producing similar dynamics. In this work, we focus on the case of a canonical regression problem under the standard normal distribution and use a coupled dynamical system to mimic the gradient descent method in the sense of a continuous-time limit, then use the high order moment tensor of the normal distribution to simplify these ordinary differential equations. The simplified system yields unexpected fixed points. The existence of these non-global-optimal stable points leads to the existence of saddle points in the loss surface of the quadratic networks. Our analysis shows there are conserved quantities during the training of the quadratic networks. Such quantities might result in a failed learning process if the network is initialized improperly. Finally, We illustrate the comparison between the numerical learning curves and the theoretical one, which reveals the two alternately appearing stages of the learning process.
Similar content being viewed by others
References
Collobert R, Weston J. A unified architecture for natural language processing: deep neural networks with multitask learning. In: Proceedings of International Conference on Machine Learning. 2008, 160–167
Krizhevsky A, Sutskever I, Hinton G E. ImageNet classification with deep convolutional neural networks. In: Proceedings of Advances in Neural Information Processing Systems. 2012, 1106–1114
He K M, Zhang X Y, Ren S Q, Sun J. Deep residual learning for image recognition. In: Proceedings of IEEE Conference on Computer Vision and Pattern Recognition. 2016, 770–778
Silver D, Schrittwieser J, Simonyan K, Antonoglou I, Huang A, Guez A, Hubert T, Baker L, Lai M, Bolton A and others. Mastering the game of go without human knowledge. Nature, 2017, 550(7676): 354–359
Li H, Xu Z, Taylor G, Studer C, Goldstein T. Visualizing the loss landscape of neural nets. In: Proceedings of Advances in Neural Information Processing Systems. 2018, 6391–6401
Hochreiter S, Schmidhuber J. Flat minima. Neural Computation, 1997, 9(1): 1–42
Yu B, Zhang J Z, Zhu Z X. On the learning dynamics of two-layer nonlinear convolutional neural networks. 2019, arXiv preprint arXiv:1905.10157
Fan F L, Xiong J J, Wang G. Universal approximation with quadratic deep networks. Neural Networks, 2020, 124: 383–392
Livni R, Shalev-Shwartz S, Shamir O. On the computational efficiency of training neural networks. In: Proceedings of Advances in Neural Information Processing Systems. 2014, 855–863
Soltani M, Hegde C. Towards provable learning of polynomial neural networks using low-rank matrix estimation. In: Proceedings of International Conference on Artificial Intelligence and Statistics. 2018, 1417–1426
Baldi P, Hornik K. Neural networks and principal component analysis: learning from examples without local minima. Neural Networks, 1989, 2(1): 53–58
Saxe A M, McClelland J L, Ganguli S. Learning hierarchical categories in deep neural networks. In: Proceedings of Annual Meeting of the Cognitive Science Society. 2013, 35(35)
Saxe A M, McClelland J L, Ganguli S. Exact solutions to the nonlinear dynamics of learning in deep linear neural networks. In: Proceedings of International Conference on Learning Representations. 2014
Jian M W, Lam K M, Dong J Y. Illumination-insensitive texture discrimination based on illumination compensation and enhancement. Information Sciences, 2014, 269: 60–72
Jian M W, Yin Y L, Dong J Y, Zhang W Y. Comprehensive assessment of non-uniform illumination for 3D heightmap reconstruction in outdoor environments. Computers in Industry, 2018, 99: 110–118
Heskes T M, Kappen B. On-line learning processes in artificial neural networks. North-Holland Mathematical Library, 1993, 51: 199–233
Zhang C Y, Bengio S, Hardt M, Recht B, Vinyals O. Understanding deep learning requires rethinking generalization. In: Proceedings of International Conference on Learning Representations. 2017
Kleinberg R, Li Y Z, Yuan Y. An alternative view: when does SGD escape local minima? In: Proceedings of International Conference on Machine Learning. 2018, 2703–2712
Advani M S, Saxe A M. High-dimensional dynamics of generalization error in neural networks. 2017, arXiv preprint arXiv:1710.03667
Neyshabur B, Tomioka R, Srebro N. In search of the real inductive bias: on the role of implicit regularization in deep learning. In: Proceedings of International Conference on Learning Representations. 2015
Pérez G V, Camargo C Q, Louis A A. Deep learning generalizes because the parameter-function map is biased towards simple functions. In: Proceedings of International Conference on Learning Representations. 2019
Du S S, Lee J D. On the power of over-parametrization in neural networks with quadratic activation. In: Proceedings of International Conference on Machine Learning. 2018, 1328–1337
Gamarnik D, Kizildag E C, Zadik I. Stationary points of shallow neural networks with quadratic activation function. 2019, arXiv preprint arXiv: 1912.01599
Acknowledgements
The authors would like to thank the support from National Natural Science Foundation of China (Grant No. 61672281).
Author information
Authors and Affiliations
Corresponding author
Additional information
Zhenghao Tan received the BS degree in information and computing science from Nanjing University of Aeronautics and Astronautics (NUAA), China in 2018. He is now studying for his MS degree in NUAA, and his research interests include machine learning and pattern recognition.
Songcan Chen received the BS degree from Hangzhou University (now merged into Zhejiang University), China, the MS degree from Shanghai Jiao Tong University, China, and the PhD degree from Nanjing University of Aeronautics and Astronautics (NUAA), China in 1983, 1985, and 1997, respectively. He joined in NUAA, China in 1986, and he has been a full-time professor with the Department of Computer Science and Engineering since 1998. He has authored/coauthored over 170 scientific peer-reviewed papers and ever obtained Honorable Mentions of 2006, 2007, and 2010 Best Paper Awards of Pattern Recognition Journal respectively. His current research interests include pattern recognition, machine learning, and neural computing.
Electronic supplementary material
Rights and permissions
About this article
Cite this article
Tan, Z., Chen, S. On the learning dynamics of two-layer quadratic neural networks for understanding deep learning. Front. Comput. Sci. 16, 163313 (2022). https://doi.org/10.1007/s11704-020-0298-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s11704-020-0298-0