Skip to main content

Advertisement

Springer Nature Link
Log in

A simple construction of CRT-based ideal secret sharing scheme and its security extension based on common factor

  • Research Article
  • Published:
Frontiers of Computer Science Aims and scope Submit manuscript

Abstract

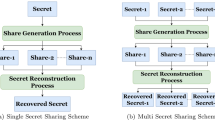
Secret sharing (SS) is part of the essential techniques in cryptography but still faces many challenges in efficiency and security. Currently, SS schemes based on the Chinese Remainder Theorem (CRT) are either low in the information rate or complicated in construction. To solve the above problems, 1) a simple construction of an ideal (t, n)-SS scheme is proposed based on CRT for a polynomial ring. Compared with Ning’s scheme, it is much more efficient in generating n pairwise coprime modular polynomials during the scheme construction phase. Moreover, Shamir’s scheme is also a special case of our scheme. To further improve the security, 2) a common-factor-based (t, n)-SS scheme is proposed in which all shareholders share a common polynomial factor. It enables both the verification of received shares and the establishment of a secure channel among shareholders during the reconstruction phase. As a result, the scheme is resistant to eavesdropping and modification attacks by outside adversaries.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Shamir A. How to share a secret. Communications of the ACM, 1979, 22(11): 612–613

    Article  MathSciNet  MATH  Google Scholar 

  2. Blakley G R. Safeguarding cryptographic keys. In: Proceedings of the National Computer Conference. 1979, 313–317

  3. Zhang X, Xu C, Zhang W, Li W. Threshold public key encryption scheme resilient against continual leakage without random oracles. Frontiers of Computer Science, 2013, 7(6): 955–968

    Article  MathSciNet  MATH  Google Scholar 

  4. Zhang Y, He D, Zhang M, Choo K K. A provable-secure and practical two-party distributed signing protocol for SM2 signature algorithm. Frontiers of Computer Science, 2020, 14(3): 1–4

    Article  Google Scholar 

  5. Roy P. A homomorphism based zero knowledge proof of authentication for chinese remainder theorem based secret sharing. In: Proceedings of Annual Convention of the Computer Society of India. 2018, 562–572

  6. Mignotte M. How to share a secret. In: Proceedings of Workshop on Cryptography 1982, 371–375

  7. Asmuth C, Bloom J. A modular approach to key safeguarding. IEEE Transactions on Information Theory, 1983, 29(2): 208–210

    Article  MathSciNet  MATH  Google Scholar 

  8. Tiplea F L, Dragan C C. Asymptotically ideal CRT-based secret sharing schemes for multilevel and compartmented access structures. IACR Cryptology ePrint Archive, 2018, 2018: 933

    Google Scholar 

  9. Shyu S J, Chen Y R. Threshold secret image sharing by Chinese remainder theorem. In: Proceedings of IEEE Asia-Pacific Services Computing Conference. 2008, 1332–1337

  10. Yan X, Lu Y, Liu L, Wan S, Ding W, Liu H. Chinese remainder theorem-based secret image sharing for (k, n) threshold. In: Proceedings of International Conference on Cloud Computing and Security. 2017, 433–440

  11. Meng K, Miao F, Yu Y, Lu C. A universal secret sharing scheme with general access structure based on CRT. In: Proceedings of the 17th IEEE International Conference on Trust, Security And Privacy In Computing And Communications/12th IEEE International Conference on Big Data Science And Engineering. 2018, 142–148

  12. Brickell E F. Some ideal secret sharing schemes. In: Proceedings of Workshop on the Theory and Application of Cryptographic Techniques. 1989, 468–475

  13. Ning Y, Miao F, Huang W, Meng K, Xiong Y, Wang X. Constructing ideal secret sharing schemes based on chinese remainder theorem. In: Proceedings of International Conference on the Theory and Application of Cryptology and Information Security. 2018, 310–331

  14. Mahmood K, Chaudhry S A, Naqvi H, Shon T, Ahmad H F. A lightweight message authentication scheme for Smart Grid communications in power sector. Computers & Electrical Engineering, 2016, 52: 114–124

    Article  Google Scholar 

  15. Gopal V, Brandt J W. Keyed-hash message authentication code processors, methods, systems, and instructions. U.S. Patent 10, 313, 129. 2019-6-4

  16. Alomair B S. Residue message authentication code. U.S. Patent 10, 243, 744. 2019-3-26

  17. Diffie W, Hellman M. New directions in cryptography. IEEE transactions on Information Theory, 1976, 22(6): 644–654

    Article  MathSciNet  MATH  Google Scholar 

  18. Barker E, Chen L, Keller S, Roginsky A, Vassilev A, Pavis R. Recommendation for pair-wise key-establishment schemes using discrete logarithm cryptography. National Institute of Standards and Technology, 2017

  19. Li P, Liu Z, Yang C N. A construction method of (t, k, n)-essential secret image sharing scheme. Signal Processing: Image Communication, 2018, 65: 210–220

    Google Scholar 

  20. Chen H, Chang C C. A novel secret sharing scheme based upon euler’s theorem. Security and Communication Networks, 2019, 2019: 2387358

    Article  Google Scholar 

  21. Kawachi A, Okamoto Y, Tanaka K, Yasunaga K. General constructions of rational secret sharing with expected constant-round reconstruction. The Computer Journal, 2017, 60(5): 711–728

    MathSciNet  Google Scholar 

  22. Zhao J, Zhang J, Zhao R. A practical verifiable multi-secret sharing scheme. Computer Standards & Interfaces, 2007, 29(1): 138–141

    Article  Google Scholar 

  23. Harn L, Hsu C F. (t, n) multi-secret sharing scheme based on bivariate polynomial. Wireless Personal Communications, 2017, 95(2): 1495–1504

    Article  Google Scholar 

  24. Hedayat A S, Sloane N J A, Stufken J. Orthogonal Arrays: Theory and Applications. Springer Science & Business Media, 2012

  25. Pieprzyk J, Zhang X M. Characterisations of ideal threshold schemes. Discrete Mathematics and Theoretical Computer Science, 2004, 6(2): 471–482

    MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

This work was supported by National Key R&D Project 2018YFB2100300 and the National Natural Science Foundation of China (Grant No. 61520106007).

Author information

Authors and Affiliations

  1. School of Computer Science and Technology, University of Science and Technology of China, Hefei, 230026, China

    Lei Wu, Fuyou Miao, Keju Meng & Xu Wang

Authors
  1. Lei Wu
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Fuyou Miao
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Keju Meng
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. Xu Wang
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Fuyou Miao.

Additional information

Lei Wu is a master student studying in the School of Computer Science and Technology in University of Science and Technology of China, China. She received bachelor’s degree in information security from Hefei University of Technology, China in 2018. Her research interests include secret sharing and Internet of Things.

Fuyou Miao received the PhD degree in computer science from University of Science and Technology of China, China, where he is an associate professor currently with the School of Computer Science and Technology. His research interests include information security, information coding key management in WSN, and network security.

Keju Meng is a PhD student studying in the School of Computer Science and Technology, University of Science and Technology of China, China. He received bachelor’s degree from Dalian Universiry of Technology, China in 2016. Now, his research interests include Internet of things, network security and secret sharing.

Xu Wang received her bachelor’s degree from China University of Geosciences, China in 2019. After that, she has been studying for a master’s degree at the University of Science and Technology of China, China. Her main research interests are secret sharing and coding.

Electronic Supplementary Material

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Wu, L., Miao, F., Meng, K. et al. A simple construction of CRT-based ideal secret sharing scheme and its security extension based on common factor. Front. Comput. Sci. 16, 161811 (2022). https://doi.org/10.1007/s11704-021-0483-9

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s11704-021-0483-9

Keywords