Skip to main content
Springer Nature Link
Log in

A new design of parity-preserving reversible multipliers based on multiple-control toffoli synthesis targeting emerging quantum circuits

  • Research Article
  • Published:
Frontiers of Computer Science Aims and scope Submit manuscript

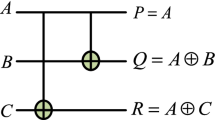
Abstract

With the recent demonstration of quantum computers, interests in the field of reversible logic synthesis and optimization have taken a different turn. As every quantum operation is inherently reversible, there is an immense motivation for exploring reversible circuit design and optimization. When it comes to faults in circuits, the parity-preserving feature donates to the detection of permanent and temporary faults. In the context of reversible circuits, the parity-preserving property ensures that the input and output parities are equal. In this paper we suggest six parity-preserving reversible blocks (Z, F, A, T, S, and L) with improved quantum cost. The reversible blocks are synthesized using an existing synthesis method that generates a netlist of multiple-control Toffoli (MCT) gates. Various optimization rules are applied at the reversible circuit level, followed by transformation into a netlist of elementary quantum gates from the NCV library. The designs of full-adder and unsigned and signed multipliers are proposed using the functional blocks that possess parity-preserving properties. The proposed designs are compared with state-of-the-art methods and found to be better in terms of cost of realization. Average savings of 25.04%, 20.89%, 21.17%, and 51.03%, and 18.59%, 13.82%, 13.82%, and 27.65% respectively, are observed for 4-bit unsigned and 5-bit signed multipliers in terms of quantum cost, garbage output, constant input, and gate count as compared to recent works.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Landauer R. Irreversibility and heat generation in the computing process. IBM Journal of Research and Development, 1961, 5(3): 183–191

    Article  MathSciNet  Google Scholar 

  2. Bennett C H. Logical reversibility of computation. IBM Journal of Research and Development, 1973, 17(6): 525–532

    Article  MathSciNet  Google Scholar 

  3. Maslov D, Dueck G W. Reversible cascades with minimal garbage. IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems, 2004, 23(11): 1497–1509

    Article  Google Scholar 

  4. Barenco A, Bennett C H, Cleve R, DiVincenzo D P, Margolus N, Shor P, Sleator T, Smolin J A, Weinfurter H. Elementary gates for quantum computation. Physical Review A, 1995, 52(5): 3457–3467

    Article  Google Scholar 

  5. Zulehner A, Paler A, Wille R. An efficient methodology for mapping quantum circuits to the IBM QX architectures. IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems, 2018, 38(7): 1226–1236

    Article  Google Scholar 

  6. Niemann P, Bandyopadhyay C, Drechsler R. Combining SWAPs and remote toffoli gates in the mapping to IBM QX architectures. In: Proceedings of 2021 Design, Automation & Test in Europe Conference & Exhibition (DATE). 2021, 200–205

  7. Parhami B. Fault-tolerant reversible circuits. In: Proceedings of the 40th Asilomar Conference on Signals, Systems and Computers. 2006, 1726–1729

  8. Muñoz-Coreas E, Thapliyal H. Quantum circuit design of a t-count optimized integer multiplier. IEEE Transactions on Computers, 2018, 68(5): 729–739

    Article  MathSciNet  Google Scholar 

  9. Bose A, Sarker A. A novel approach for constructing reversible fault tolerant n-bit binary comparator. In: Proceedings of 2014 International Conference on Informatics, Electronics & Vision (ICIEV). 2014, 1–6

  10. Bruce J W, Thornton M A, Shivakumaraiah L, Kokate P S, Li X. Efficient adder circuits based on a conservative reversible logic gate. In: Proceedings of IEEE Computer Society Annual Symposium on VLSI. New Paradigms for VLSI Systems Design. ISVLSI 2002. 2002, 83–88

  11. Haghparast M, Navi K. Design of a novel fault tolerant reversible full adder for nanotechnology based systems. World Applied Sciences Journal, 2008, 3(1): 114–118

    Google Scholar 

  12. Qi X, Chen F, Zuo K, Guo L, Luo Y, Hu M. Design of fast fault tolerant reversible signed multiplier. International Journal of the Physical Sciences, 2012, 7(17): 2506–2514

    Google Scholar 

  13. Islam S, Begum Z. Reversible logic synthesis of fault tolerant carry skip BCD adder. 2010, arXiv preprint arXiv: 1008.3288

  14. Qi X, Chen F, Guo L, Luo Y, Hu M. Efficient approaches for designing fault tolerant reversible BCD adders. Journal of Computational Information Systems, 2013, 9(14): 5869–5877

    Google Scholar 

  15. Mitra S K, Chowdhury A R. Minimum cost fault tolerant adder circuits in reversible logic synthesis. In: Proceedings of the 25th International Conference on VLSI Design. 2012, 334–339

  16. Shoaei S, Haghparast M. Novel designs of nanometric parity preserving reversible circuits. In: Proceedings of 8th Symposium on Advances in Science and Technology. 2013

  17. Shoaei S, Haghparast M. Novel designs of nanometric parity preserving reversible compressor. Quantum Information Processing, 2014, 13(8): 1701–1714

    Article  Google Scholar 

  18. Valinataj M, Mirshekar M, Jazayeri H. Novel low-cost and fault-tolerant reversible logic adders. Computers & Electrical Engineering, 2016, 53: 56–72

    Article  Google Scholar 

  19. Misra N K, Sen B, Wairya S. Novel tree structure based conservative reversible binary coded decimal adder and sequential circuit with added high testability. Journal of Computational and Theoretical Nanoscience, 2017, 14(5): 2515–2527

    Article  Google Scholar 

  20. Sen B, Dutta M, Banik D, Singh D K, Sikdar B K. Design of fault tolerant reversible arithmetic logic unit in QCA. In: Proceedings of 2012 International Symposium on Electronic System Design (ISED). 2012, 241–245

  21. Sen B, Ganeriwal S, Sikdar B K. Reversible logic-based fault-tolerant nanocircuits in QCA. International Scholarly Research Notices, 2013, 2013: 850267

    Google Scholar 

  22. Zhou R G, Li Y C, Zhang M Q. Novel designs for fault tolerant reversible binary coded decimal adders. International Journal of Electronics, 2014, 101(10): 1336–1356

    Article  Google Scholar 

  23. PourAliAkbar E, Navi K, Haghparast M, Reshadi M. Novel optimum parity-preserving reversible multiplier circuits. Circuits, Systems, and Signal Processing, 2020, 39(10): 5148–5168

    Article  Google Scholar 

  24. Jamal L, Rahman M, Babu H M H. An optimal design of a fault tolerant reversible multiplier. In: Proceedings of 2013 IEEE International SOC Conference. 2013, 37–42

  25. Babazadeh S, Haghparast M. Design of a nanometric fault tolerant reversible multiplier circuit. Journal of Basic and Applied Scientific Research, 2012, 2(2): 1355–1361

    Google Scholar 

  26. Valinataj M. Novel parity-preserving reversible logic array multipliers. The Journal of Supercomputing, 2017, 73(11): 4843–4867

    Article  Google Scholar 

  27. Chowdhury E S, Ahmed N, Jamal L. A new perspective in designing an optimized fault tolerant reversible multiplier. In: Proceedings of Joint the 8th International Conference on Informatics, Electronics & Vision (ICIEV) and the 3rd International Conference on Imaging, Vision & Pattern Recognition (icIVPR). 2019, 274–279

  28. Gaur H M, Singh A K, Ghanekar U. An efficient design of scalable reversible multiplier with testability. Journal of Circuits, Systems and Computers, 2022, 31(10): 2250179

    Article  Google Scholar 

  29. PourAliAkbar E, Navi K, Haghparast M, Reshadi M. Novel designs of fast parity-preserving reversible vedic multiplier. The CSI Journal on Computer Science and Engineering, 2019, 17(1): 9–20

    Google Scholar 

  30. Gaur H M, Singh A K, Ghanekar U. Testable design of reversible circuits using parity preserving gates. IEEE Design & Test, 2018, 35(4): 56–64

    Article  Google Scholar 

  31. Gaur H M, Singh A K, Ghanekar U. Design of reversible arithmetic logic unit with built-in testability. IEEE Design & Test, 2019, 36(5): 54–61

    Article  Google Scholar 

  32. Gaur H M, Singh A K, Mohan A, Fujita M, Pradhan D K. Design of single-bit fault-tolerant reversible circuits. IEEE Design & Test, 2021, 38(2): 89–96

    Article  Google Scholar 

  33. Gaur H M, Singh A K, Ghanekar U. Simplification and modification of multiple controlled Toffoli circuits for testability. Journal of Computational Electronics, 2019, 18(1): 356–363

    Article  Google Scholar 

  34. Gaur H M, Singh A K. Design of reversible circuits with high testability. Electronics Letters, 2016, 52(13): 1102–1104

    Article  Google Scholar 

  35. Noorallahzadeh M, Mosleh M, Ahmadpour S S, Pal J, Sen B. A new design of parity preserving reversible Vedic multiplier targeting emerging quantum circuits. International Journal of Numerical Modelling: Electronic Networks, Devices and Fields, 2023, e3089

  36. Noorallahzadeh M, Mosleh M, Misra N K, Mehranzadeh A. A novel design of reversible quantum multiplier based on multiple-control toffoli synthesis. Quantum Information Processing, 2023, 22(4): 167

    Article  MathSciNet  Google Scholar 

  37. Gaur H M, Singh A K, Ghanekar U. Design for stuck-at fault testability in toffoli-fredkin reversible circuits. National Academy Science Letters, 2021, 44(3): 215–220

    Article  MathSciNet  Google Scholar 

  38. Singh A K, Gaur H M, Ghanekar U. Fault detection in multiple controlled Fredkin circuits. IET Circuits, Devices & Systems, 2019, 13(5): 723–729

    Article  Google Scholar 

  39. Gaur H M, Singh A K, Ghanekar U. Offline testing of reversible logic circuits: an analysis. Integration, 2018, 62: 50–67

    Article  Google Scholar 

  40. Gaur H M, Singh A K, Ghanekar U. Reversible circuits with testability using quantum controlled-not and swap gates. Indian Journal of Pure & Applied Physics, 2018, 56: 529–532

    Google Scholar 

  41. Gaur H M, Singh A K, Ghanekar U. A new DFT methodology for k-CNOT reversible circuits and its implementation using quantum-dot cellular automata. Optik, 2016, 127(22): 10593–10601

    Article  Google Scholar 

  42. Gaur H M, Singh A K, Ghanekar U. A comprehensive and comparative study on online testability for reversible logic. Pertanika Journal of Science & Technology, 2016, 24(2): 245–271

    Google Scholar 

  43. Thapliyal H, Ranganathan N. A new reversible design of BCD adder. In: Proceedings of 2011 Design, Automation & Test in Europe. 2011, 1–4

  44. Feynman R P. Quantum mechanical computers. Optics News, 1985, 11(2): 11–20

    Article  Google Scholar 

  45. Toffoli T. Reversible computing. In: Proceedings of the 7th International Colloquium on Automata, Languages, and Programming. 1980, 632–644

  46. Miller D M, Maslov D, Dueck G W. A transformation based algorithm for reversible logic synthesis. In: Proceedings of 2003 Design Automation Conference. 2003, 318–323

  47. Kole A, Hillmich S, Datta K, Wille R, Sengupta I. Improved mapping of quantum circuits to IBM QX architectures. IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems, 2020, 39(10): 2375–2383

    Article  Google Scholar 

  48. Rahman M, Banerjee A, Dueck G W, Pathak A. Two-qubit quantum gates to reduce the quantum cost of reversible circuit. In: Proceedings of the 41st IEEE International Symposium on Multiple-Valued Logic. 2011, 86–92

  49. Lewandowski M, Ranganathan N, Morrison M. Behavioral model of integrated qubit gates for quantum reversible logic design. In: Proceedings of 2013 IEEE Computer Society Annual Symposium on VLSI (ISVLSI). 2013, 194–199

  50. Hung W N N, Song X Y, Yang G W, Yang J, Perkowski M. Optimal synthesis of multiple output Boolean functions using a set of quantum gates by symbolic reachability analysis. IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems, 2006, 25(9): 1652–1663

    Article  Google Scholar 

  51. Rahman M, Dueck G W. Properties of quantum templates. In: Proceedings of the 4th International Workshop on Reversible Computation. 2012, 125–137

  52. Maslov D, Dueck G W, Miller D M. Toffoli network synthesis with templates. IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems, 2005, 24(6): 807–817

    Article  Google Scholar 

  53. Soeken M, Sasanian Z, Wille R, Miller D M, Drechsler R. Optimizing the mapping of reversible circuits to four-valued quantum gate circuits. In: Proceedings of the 42nd IEEE International Symposium on Multiple-Valued Logic. 2012, 173–178

  54. Shende V V, Prasad A K, Markov I L, Hayes J P. Synthesis of reversible logic circuits. IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems, 2003, 22(6): 710–722

    Article  Google Scholar 

  55. Miller D M, Soeken M, Drechsler R. Mapping NCV circuits to optimized Clifford+T circuits. In: Proceedings of the 6th International Conference on Reversible Computation. 2014, 163–175

  56. Soeken M, Thomsen M K. White dots do matter: rewriting reversible logic circuits. In: Proceedings of the 5th International Conference on Reversible Computation. 2013, 196–208

  57. Fredkin E, Toffoli T. Conservative logic. International Journal of Theoretical Physics, 1982, 21(3–4): 219–253

    Article  MathSciNet  Google Scholar 

  58. Parhami B. Computer Arithmetic: Algorithms and Hardware Designs. 2nd ed. New York: Oxford University Press, 2010

    Google Scholar 

  59. Baugh C R, Wooley B A. A two’s complement parallel array multiplication algorithm. IEEE Transactions on Computers, 1973, C-22(12): 1045–1047

    Article  Google Scholar 

  60. Tan T R, Gaebler J P, Lin Y, Wan Y, Bowler R, Leibfried D, Wineland D J. Multi-element logic gates for trapped-ion qubits. Nature, 2015, 528(7582): 380–383

    Article  Google Scholar 

  61. Kole A, Datta K, Sengupta I. A new heuristic for N-dimensional nearest neighbor realization of a quantum circuit. IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems, 2018, 37(1): 182–192

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Computer Engineering, Dezful Branch, Islamic Azad University, Dezful, Iran

    Mojtaba Noorallahzadeh & Mohammad Mosleh

  2. German Research Centre for Artificial Intelligence (DFKI), Bremen, 28359, Germany

    Kamalika Datta

  3. Institute of Computer Science, University of Bremen, Bremen, 28359, Germany

    Kamalika Datta

Authors
  1. Mojtaba Noorallahzadeh
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Mohammad Mosleh
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Kamalika Datta
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding authors

Correspondence to Mojtaba Noorallahzadeh or Mohammad Mosleh.

Ethics declarations

Competing interests The authors declare that they have no competing interests or financial conflicts to disclose.

Additional information

Mojtaba Noorallahzadeh received the BS degree in Computer Software Engineering Technology from Mehestan Sabz North Tonkabon Higher Applied Scientific Education Center, Iran in 2011, and the MS degree in Architecture of Computer Systems from Islamic Azad University, Iran in 2018. His research interests include the synthesis and optimization of reversible and quantum circuits, quantum-dot cellular automata (QCA), Internet of Things (IoT), and embedded systems.

Mohammad Mosleh received the BS degree in Computer Hardware Engineering from Islamic Azad University, Iran in 2003, the MS degree in Architecture of Computer Systems from Islamic Azad University, Science and Research Branch, Iran in 2006 as well as the PhD degree in Computer Engineering from the Islamic Azad University, Science and Research Branch, Tehran, Iran in 2010. He is an associate professor in the Department of Computer Engineering at the Islamic Azad University, Iran. His research interests are in audio security (watermarking and steganography), nano computing including quantum-dot cellular automata (QCA) and reversible circuits.

Kamalika Datta completed her Master of Science (MS) from Indian Institute of Technology Kharagpur, India in 2010, and PhD from Indian Institute of Engineering Science and Technology (IIEST), India in 2014. She joined the National Institute of Technology Meghalaya, India as an assistant professor in the Department of Computer Science and Engineering in 2014. She is presently working as a researcher at the University of Bremen, Germany. She has published more than 80 papers in peer-reviewed journals and conferences. Her research interests include logic design using emerging technologies, synthesis and optimization of reversible and quantum circuits, and embedded systems.

Electronic supplementary material

11704_2023_2492_MOESM1_ESM.pdf

A New Design of Parity Preserving Reversible Multipliers Based on Multiple-Control Toffoli Synthesis Targeting Emerging Quantum Circuits

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Noorallahzadeh, M., Mosleh, M. & Datta, K. A new design of parity-preserving reversible multipliers based on multiple-control toffoli synthesis targeting emerging quantum circuits. Front. Comput. Sci. 18, 186908 (2024). https://doi.org/10.1007/s11704-023-2492-3

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s11704-023-2492-3

Keywords