Skip to main content
Springer Nature Link
Log in

Solving multi-criteria problems under risk: an approach explained using the example of rescheduling in dynamic environments

  • Production Management
  • Published:
Production Engineering Aims and scope Submit manuscript

Abstract

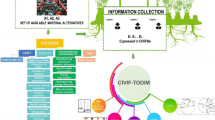
There is a decent number of possible heuristic methods to solve an actual problem in production planning and control. Usually, each solving method leads to a different alternative. In dynamic production environments, decision makers often have to decide between uncertainty and risk. Making multi-criteria decisions under risk is a well-known problem. In this paper, we will consider rescheduling as an example for decision-making in a dynamic production environment. It is used to present an intelligent manufacturing approach for multi-criteria decisions under risk that combines a method for decision-making under risk and a multi-attribute decision-making method. Moreover, for frequently appearing problems, such as rescheduling, a procedure to evaluate the used solving methods is presented. We use this information to achieve a sustainable improvement for the solving procedure of future manufacturing problems.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4

Similar content being viewed by others

References

  1. Aytug H et al (2005) Executing production schedules in the face of uncertainties: a review and some future directions. Eur J Oper Res 161:86–110

    Article  MATH  MathSciNet  Google Scholar 

  2. Blohm H, Lüder K, Schaefer C (2012) Investition –Schwachstellen-analyse des Investitionsbereichs und Investitionsrechnung. Vahlen, Franz, München

    Google Scholar 

  3. Butler J, Jia J, Dyer J (1997) Simulation techniques for the sensitivity analysis of multi-criteria decision models. Eur J Oper Res 103:531–546

    Article  MATH  Google Scholar 

  4. Götze U (2008) Investitionsrechnung - Modelle und Analysen zur Beurteilung von Investitionsvorhaben. Springer-Verlag, Berlin

    Google Scholar 

  5. Guitouni A, Martel J (1998) Tentative guidelines to help choosing an appropriate MCDA method. Eur J Oper Res 109:501–521

    Article  MATH  Google Scholar 

  6. Herroelen W, Leus R (2005) Project scheduling under uncertainty: survey and research potentials. Eur J Oper Res 165:289–306

    Article  MATH  Google Scholar 

  7. Horn J (1997) Multicriterion decision making. Handbook of evolutionary computation. Oxford, IOP Publishing and Oxford University Press, pp F1.9:1–F1.9:15

    Google Scholar 

  8. Hwang C, Yoon K (1981) Multiple attribute decision making methods and applications: a state-of-the-art survey. Springer, Berlin

    Book  MATH  Google Scholar 

  9. Katragjini K, Vallada E, Ruiz R (2013) Flow shop rescheduling under different types of disruption. Int J Prod Res 51(3):780–797

    Article  Google Scholar 

  10. Kempf K, Uzsoy R, Smith S, Garty K (2000) Evaluation and comparison of production schedules. Comput Ind 42:203–220

    Article  Google Scholar 

  11. Laaribi A, Chevallier J, Martel J (1996) A spatial decision aid—a multicriterion evaluation approach. Comput Environ Urban Syst 20(6):351–366

    Article  Google Scholar 

  12. Matos M (2007) Decision under risk as a multicriteria problem. Eur J Oper Res 181:1516–1529

    Article  MATH  Google Scholar 

  13. Roy B, Bouyssou D (1991) Decision-aid: an elementary introduction with emphasis on multiple criteria. Investigación Operativa 2:95–110

    Google Scholar 

  14. Schneeweiß H (1967) Entscheidungskriterien bei Risiko. Springer, Berlin

    Book  MATH  Google Scholar 

  15. Ude J (2010) Entscheidungsunterstützung für die Konfiguration globaler Wertschöpfungsnetzwerke: Ein Bewertungsansatz unter Berücksichtigung multikriterieller Zielsysteme, Dynamik und Unsicherheit. Shaker, Aachen

    Google Scholar 

  16. Vieira G, Herrmann J, Lin E (2003) Rescheduling manufacturing systems—a framework of strategies, policies, and methods. J Sched 6:39–62

    Article  MATH  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. wbk – Institute of Production Science, Karlsruhe Institute of Technology (KIT), Kaiserstr. 12, 76131, Karlsruhe, Germany

    N. Stricker, R. Kopf & G. Lanza

Authors
  1. N. Stricker
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. R. Kopf
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. G. Lanza
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to N. Stricker.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Stricker, N., Kopf, R. & Lanza, G. Solving multi-criteria problems under risk: an approach explained using the example of rescheduling in dynamic environments. Prod. Eng. Res. Devel. 8, 535–541 (2014). https://doi.org/10.1007/s11740-014-0556-9

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11740-014-0556-9

Keywords