Skip to main content
Springer Nature Link
Log in

A non-invasive form finding method with application to metal forming

  • Computer Aided Engineering
  • Published:
Production Engineering Aims and scope Submit manuscript

Abstract

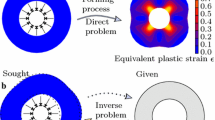
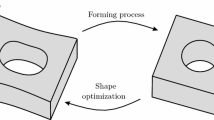
Inverse form finding aims in determining the optimal material configuration of a workpiece for a specific forming process. A gradient- and parameter-free (nodal-based) form finding approach has recently been developed, which can be coupled non-invasively as a black box to arbitrary finite element software. Additionally the algorithm is independent from the constitutive behavior. Consequently, the user has not to struggle with the underlying optimization theory behind. Benchmark tests showed already that the approach works robustly and efficiently. This contribution demonstrates that the optimization algorithm is also applicable to more sophisticated forming processes including orthotropic large strain plasticity, combined hardening and frictional contact. A cup deep drawing process with solid-shell elements and a combined deep drawing and upsetting process to form a functional component with external teeth are investigated.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16

Similar content being viewed by others

References

  1. Merklein M, Allwood JM, Behrens BA, Brosius A, Hagenah H, Kuzmann K, Mori K, Tekkaya AE, Weckenmann A (2012) Bulk forming of sheet metal. CIRP Ann Manuf Technol 61(2):725–745

    Article  Google Scholar 

  2. Guo YQ, Batoz JL, Detraux JM, Duroux P (1990) Finite element procedures for strain estimations of sheet metal forming parts. Int J Numer Methods Eng 30:1385–1401

    Article  MATH  Google Scholar 

  3. Kim JY, Kim N, Huh MS (2000) Optimal blank design of an automobile subframe. J Mater Process Technol 101:31–41

    Article  Google Scholar 

  4. Padmanabhan R, Oliveira MC, Baptista AJ, Alves JL, Menezes LF (2008) Blank design of deep drawing parts using parametric NURBS surfaces. J Mater Process Technol 101:31–41

    Google Scholar 

  5. Hammami W, Padmanabhan R, Oliveira MC, BelHadjSalah H, Alves JL, Menezes LF (2009) A deformation based blank design method for formed parts. Int J Mech Mater Des 5:303–314

    Article  Google Scholar 

  6. Braibant V, Fleury C (1984) Shape optimal design using B-splines. Comput Methods Appl Mech Eng 194:3438–3452

    Google Scholar 

  7. Fourment L, Chenot JL (1990) Optimal design for non-steady-state metal forming processes—I. Shape optimization method. Int J Numer Methods Eng 39:33–50

    Article  Google Scholar 

  8. Haftka R, Grandhi R (1986) Structural shape optimization—a survey. Comput Methods Appl Mech Eng 57–1:91–106

    Article  MathSciNet  Google Scholar 

  9. Michaleris P, Tortorelli D, Vidal C (1994) Tangent operators and design sensitivity formulations for transient non-linear coupled problems with application to elastoplasticity. Int J Numer Meth Eng 37–14:2471–2499

    Article  Google Scholar 

  10. Acharjee S, Zabaras N (2006) The continuum sensitivity method for computational design of three-dimensional deformation processes. Comput Methods Appl Mech Eng 195:6822–6842

    Article  MathSciNet  MATH  Google Scholar 

  11. Govindjee S, Mihalic PA (1996) Computational methods for inverse finite elastostatics. Comput Methods Appl Mech Eng 136–1(2):47–57

    Article  Google Scholar 

  12. Germain S, Landkammer P, Steinmann P (2014) On a recursive formulation for solving inverse form finding problems in isotropic elastoplasticity. Adv Model Simul Eng 10–1:1–19. doi:10.1186/2213-7467-1-10

    Google Scholar 

  13. Landkammer P, Steinmann P (2015) A non-invasive heuristic approach to shape optimization in forming. Comput Mech. doi:10.1007/s00466-015-1226-2

    Google Scholar 

  14. Landkammer P, Steinmann P (2015) Application of a non-invasive form finding algorithm to the ring compression test with varying friction coefficients. Key Eng Mater 651:1381–1386

    Article  Google Scholar 

  15. Schneider T, Merklein M (2013) Manufacturing of geared sheet metal components by a single-stage Sheet-bulk metal forming process. In: Proceedings of conference competitive manufacturing, pp 177–182

  16. Hinton E, Campbell JS (1974) Local and global smoothing of discontinuous finite element functions using a least squares method. Int J Numer Methods Eng 8–3:461–480

    Article  MathSciNet  Google Scholar 

  17. Landkammer P, Steinmann P (2015) A global damping factor for a non-invasive form finding algorithm. Proc Appl Math Mech 15–1:327–328

    Article  Google Scholar 

  18. Grüner M, Merklein M (2014) Determination of friction coefficitions in deep drawing by modification of Siebels’s formula for calculation of ideal drawing force. Prod Eng Res Dev 8:577–584

    Article  Google Scholar 

  19. Vierzigmann U, Koch J, Merklein M, Engel U (2012) Material flow in sheet-bulk metal forming. Key Eng Mater 504:1035–1040

    Article  Google Scholar 

  20. Schmaltz S, Willner K (2014) Comparison of different biaxial tests for the inverse identification of sheet metal parameters. Strain Int J Exp Mech 50:5. doi:10.111/str.12080

    Google Scholar 

  21. Schmaltz S (2015) Inverse Materialparameter-identifikation von Blechwerkstoffen für ein anisotropes elasto-plastisches Materialmodell bei finiten Deformationen. Dissertation, Schriftenreihe Technische Mechanik 14, FAU Erlangen-Nürnberg

  22. Alves de Souza RJ, Yoon JW, Cardoso RPR, Fontes Valente RA, Gracio JJ (2007) On the use of reduced enhanced solid-shell (RESS) elements for sheet forming simulations. Int J Plast 23:490–515

    Article  Google Scholar 

  23. Löffler M, Schneider T, Vierzigmann U, Engel U, Merklein M (2015) Locally adapted tribological conditions as a method for influencing the material flow in Sheet-bulk metal forming processes. Key Eng Mater 639:267–274

    Article  Google Scholar 

  24. Hildenbrand P, Schneider T, Merklein M (2015) Flexible rolling of process adapted semi-finished parts and its application in Sheet-bulk metal forming processes. Key Eng Mater 639:259–266

    Article  Google Scholar 

  25. Yin Q, Soyarslan C, Grüner A, Brosius A, Tekkaya AE (2012) A cyclic twin bridge shear test for the identification of kinematic hardening parameters. Int J Mech Sci 59:31–43

    Article  Google Scholar 

Download references

Acknowledgments

This work was supported by the German Research Foundation (DFG) within the scope of the Transregional Collaborative Research Center on Sheet-Bulk Metal Forming (TCRC 73, https://www.tr-73.de) in the subprojects C3 (Parameter and Shape Optimization) and A1 (Deep Drawing).

Author information

Authors and Affiliations

  1. Institute of Applied Mechanics (LTM, FAU Erlangen-Nürnberg), Egerlandstrasse 5, 91058, Erlangen, Germany

    Philipp Landkammer & Paul Steinmann

  2. Institute of Manufacturing Technology (LFT, FAU Erlangen-Nürnberg), Egerlandstrasse 13, 91058, Erlangen, Germany

    Thomas Schneider, Robert Schulte & Marion Merklein

Authors
  1. Philipp Landkammer
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Thomas Schneider
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Robert Schulte
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. Paul Steinmann
    View author publications

    You can also search for this author inPubMed Google Scholar

  5. Marion Merklein
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Philipp Landkammer.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Landkammer, P., Schneider, T., Schulte, R. et al. A non-invasive form finding method with application to metal forming. Prod. Eng. Res. Devel. 10, 93–102 (2016). https://doi.org/10.1007/s11740-016-0659-6

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11740-016-0659-6

Keywords