Skip to main content
SpringerLink
Log in

What are the analytical conditions for which a blind equalizer will loose the convergence state?

  • Original Paper
  • Published:
Signal, Image and Video Processing Aims and scope Submit manuscript

Abstract

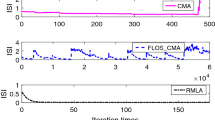
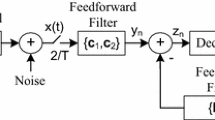
In this paper, I propose for the noiseless, real and two independent quadrature carrier case some approximated conditions on the step-size parameter, on the equalizer’s tap length and on the channel power, related to the nature of the chosen equalizer and input signal statistics, for which a blind equalizer will not converge anymore. These conditions are valid for type of blind equalizers where the error that is fed into the adaptive mechanism that updates the equalizer’s taps can be expressed as a polynomial function of the equalized output of order three like in Godard’s algorithm. Since the channel power is measurable or can be calculated if the channel coefficients are given, there is no need anymore to carry out any simulation with various step-size parameters and equalizer’s tap length for a given equalization method and input signal statistics in order to find the maximum step-size parameter for which the equalizer still converges.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Nikias, C.L., Petropulu, A.P. (eds): Higher-Order Spectra Analysis A Nonlinear Signal Processing Framework, Chapter 9, pp. 419–425. Prentice-Hall, Englewood Cliffs (1993)

    Google Scholar 

  2. Godard D.N.: Self recovering equalization and carrier tracking in two-dimensional data communication system. IEEE Trans. Commun. 28(11), 1867–1875 (1980)

    Article  Google Scholar 

  3. Sato Y.: A method of self-recovering equalization for multilevel amplitude-modulation systems. IEEE Trans. Commun. 23, 679–682 (1975)

    Article  Google Scholar 

  4. Pinchas, M.: A MSE optimized polynomial equalizer for 16QAM and 64QAM constellation. Signal Image Video Process. doi:10.1007/s11760-009-0138-z, Oct. (2009)

  5. Bellini, S.: Bussgang techniques for blind equalization. In: Proceedings of IEEE Global Telecommunication Conference Records, pp. 1634–1640. December (1986)

  6. Bellini S.: Blind equalization. Alta Frequenza 57, 445–450 (1988)

    Google Scholar 

  7. Pinchas M., Bobrovsky B.Z.: A maximum entropy approach for blind deconvolution. Signal Process. 86, 2913–2931 (2006)

    Article  MATH  Google Scholar 

  8. Haykin, S. : Blind deconvolution. In:Haykin, S. Adaptive Filter Theory, Chapter 20, Prentice-Hall, Englewood Cliffs (1991)

  9. Lee E.A., Messerschmitt D.G.: Digital Communication, 2nd edn, Chapter 11, pp. 517–538. Kluwer Academic, Boston (1997)

    Google Scholar 

  10. Nandi, A.K. (eds): Blind Estimation Using Higher-Order Statistics, Chapter 2, pp. 66. Kluwer Academic, Boston (1999)

    Google Scholar 

  11. Lazaro M., Santamaria I., Erdogmus D., Hild K.E., Pantaleon C., Principe J.C.: Stochastic blind equalization based on pdf fitting using Parzen estimator. IEEE Trans. Signal Process. 53(2), 696–704 (2005)

    Article  MathSciNet  Google Scholar 

  12. Shalvi O., Weinstein E.: New criteria for blind deconvolution of nonminimum phase systems (channels). IEEE Trans. Inf. Theor. 36(2), 312–321 (1990)

    Article  MathSciNet  MATH  Google Scholar 

  13. Gi-Hong Im., Park C.J., Won H.C.: A blind equalization with the sign algorithm for broadband access. IEEE Comm. Lett. 5(2), 70–72 (2001)

    Article  Google Scholar 

  14. Pinchas M.: A closed approximated formed expression for the achievable residual intersymbol interference obtained by blind equalizers. Signal Process. J. (Eurasip) 90(6), 1940–1962 (2010). doi:10.1016/j.sigpro.2009.12.014

    MATH  Google Scholar 

  15. Fiori S.: A contribution to (neuromorphic) blind deconvolution by flexible approximated Bayesian estimation. Signal Process. 81, 2131–2153 (2001)

    Article  Google Scholar 

  16. Godfrey R., Rocca F.: Zero memory non-linear deconvolution. Geophys. Prospect. 29, 189–228 (1981)

    Article  Google Scholar 

  17. http://spib.rice.edu/spib/microwave.html

  18. http://www.gigafast.com/Support/VDSL/vdsl/#11

  19. http://www.zyxel.com/support/supportnote/ves1012/fac/vdslfac.htm

Download references

Author information

Authors and Affiliations

  1. Department of Electrical and Electronic Engineering, Ariel University Center of Samaria, Ariel, 40700, Israel

    Monika Pinchas

Authors
  1. Monika Pinchas
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Monika Pinchas.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Pinchas, M. What are the analytical conditions for which a blind equalizer will loose the convergence state?. SIViP 6, 325–340 (2012). https://doi.org/10.1007/s11760-011-0221-0

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11760-011-0221-0

Keywords

Search

Navigation