Inter-layer correlation considered R-D models and Lagrange multiplier for SVC MGS coding

Abstract

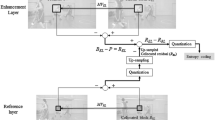
Traditional rate-distortion (R-D) model-based Lagrange multiplier $\lambda$ that is employed by H.264/SVC does not consider the inter-layer correlation. This paper presents new R-D models and $\lambda$ which exploits inter-layer correlation for coding modes that perform residual prediction in H.264/SVC medium-grain quality scalability (MGS) coding. We have observed that in MGS coding, the prediction error of modes performing residual prediction is approximately equal to the reconstruction error of the corresponding macroblock in the reference layer. Based on that observation, we investigate the distribution $f_r$ of transformed residual prediction error signals and prove that $f_r$is related to the quantization step of the corresponding macroblock in the reference layer. In such a case, both the conventional $\lambda$ and the R-D models in the literature that are derived independently of inter layers are not much fit for residual prediction modes any more. Thus, we build more appropriate R-D models depending on the derived distribution and develop a new $\lambda$ from the R-D models. Experimental results show that when residual prediction is enabled, the proposed scheme by using the new Lagrange multiplier achieves an average PSNR gain of 0.47 dB and up to more than 1 dB over the scheme using the conventional Lagrange multiplier.

Appendix

1.1 Appendix A: Derivation of equation (18)

According to domain of n,

$$\begin{aligned} {H}=-\sum {P}_{n} \text{ log}P_{n} =-{P}_0 \text{ log}P_0 -2\sum _{n=1}^\Delta {{P}_{n} \text{ log}P_{n} } \end{aligned}$$

(A1)

With the definition of ${P}_{n}$ in (16),

$$\begin{aligned} {H}&= -\frac{1\!-\!e^{-uq}}{1\!-\!e^{-ub}}\log _2 \frac{1\!-\!e^{-uq}}{1\!-\!e^{-ub}}\nonumber \\[3pt]&-2\sum \limits _{n=1}^{\Delta -1} \frac{\left( {1\!-\!e^{-uq}}\right)e^{-nuq}}{2\left( {1\!-\!e^{-ub}} \right)}\log _2 \frac{\left( {1\!-\!e^{-uq}} \right)e^{-nuq}}{2\left( {1\!-\!e^{-ub}} \right)}\nonumber \\&-\frac{e^{-\mu \Delta q}\left( {1\!-\!e^{-\mu \delta }} \right)}{\left( {1\!-\!e^{-\mu b}} \right)}\log _2 \frac{e^{-\mu \Delta q}\left( {1\!-\!e^{-\mu \delta }} \right)}{2\left({1\!-\!e^{-\mu b}} \right)}\nonumber \\&= -\frac{1\!-\!e^{-uq}}{1\!-\!e^{-ub}}\log _2 \frac{1\!-\!e^{-uq}}{1\!-\!e^{-ub}}-\!+\!\frac{\log _2 e\cdot uq}{1\!-\!e^{-ub}}\cdot \nonumber \\&\times \left\{ {\frac{e^{-uq}\!-\!\Delta e^{-\Delta uq}\!+\!\left( {\Delta \!-\!1} \right)e^{-\left( {\Delta \!+\!1} \right)uq}}{1\!-\!e^{-uq}}} \right\} \nonumber \\&-\frac{e^{-uq}\!-\!e^{-\Delta uq}}{1\!-\!e^{-ub}}\log _2 \frac{1\!-\!e^{-uq}}{2\left( {1\!-\!e^{-ub}} \right)}\nonumber \\&-\frac{e^{-\mu \Delta q}\left( {1\!-\!e^{-\mu \delta }} \right)}{\left( {1\!-\!e^{-\mu b}} \right)}\log _2 \frac{e^{-\mu \Delta q}\left( {1\!-\!e^{-\mu \delta }} \right)}{2\left( {1\!-\!e^{-\mu b}} \right)}\nonumber \\&= \frac{e^{-uq}\!-\!e^{-\Delta uq}}{1\!-\!e^{-ub}}\!+\!\frac{e^{-\Delta uq}\!-\!1}{1\!-\!e^{-ub}}\log _2 \frac{1\!-\!e^{-uq}}{1\!-\!e^{-ub}}\!+\!\frac{\log _2 e\cdot uq}{1\!-\!e^{-ub}}\cdot \nonumber \\&\times \left\{ {\frac{e^{-uq}\!-\!\Delta e^{-\Delta uq}\!+\!\left( {\Delta \!-\!1} \right)e^{-\left( {\Delta \!+\!1} \right)uq}}{1\!-\!e^{-uq}}} \right\} \nonumber \\&-\frac{e^{-\mu \Delta q}\left( {1\!-\!e^{-\mu \delta }} \right)}{\left( {1\!-\!e^{-\mu b}} \right)}\log _2 \frac{e^{-\mu \Delta q}\left( {1\!-\!e^{-\mu \delta }} \right)}{2\left( {1\!-\!e^{-\mu b}} \right)} \end{aligned}$$

(A2)

1.2 Appendix B: Derivation of Equation (21)

With (15), Eq. (20) can be rewritten as:

$$\begin{aligned} \text{ D}&= \frac{1}{\left( {1-\text{ e}^{-\mu {Q}_{b} }} \right)}\cdot \left( \int \limits _{\Delta {Q}_{e} }^{\Delta {Q}_{e} +\delta } \left( {\text{ y}-\Delta \text{ Q}_{e}} \right)^{2}\cdot \mu \text{ e}^{-\mu \text{ y}}\text{ dy}\right.\nonumber \\&\left.+\sum \limits _{{i}=0}^{\Delta -1} \int \limits _{{iQ}_{e} }^{{iQ}_{e} +{Q}_{e} } \left( {\text{ y}-\text{ iQ}_{e} } \right)^{2}\cdot \mu \text{ e}^{-\mu \text{ y}}\text{ dy} \right)\nonumber \\&= \frac{1}{\left( {1-\text{ e}^{-\mu {Q}_{b} }} \right)}\cdot (\text{ D}_{a} +\text{ D}_{b} ) \end{aligned}$$

(B1)

where

$$\begin{aligned} \text{ D}_{a}&= \int \limits _{\Delta {Q}_{e} }^{\Delta {Q}_{e} +\delta } \left( {{y}-\Delta {Q}_{e} } \right)^{2}\cdot \mu \text{ e}^{-\mu \left( {\text{ y}-\Delta \text{ Q}_{e} +\Delta {Q}_{e} } \right)}\text{ d}y\nonumber \\&= \int \limits _{\Delta \text{ Q}_{e} }^{\Delta { Q}_{e} +\delta } \left( {{y}-\Delta {Q}_{e} } \right)^{2}\cdot \mu \text{ e}^{-\mu \left( {{y}-\Delta { Q}_{e} +\Delta {Q}_{e}} \right)}\text{ d}y \nonumber \\&= \text{ e}^{-\mu \Delta {Q}_{e} }\int \limits _0^\delta {y}^{\prime 2}\cdot \mu \text{ e}^{-\mu { y}^{\prime }}\text{ dy}^{\prime }\nonumber \\&= \text{ e}^{-\mu \Delta \text{ Q}_{e} }\left( {\frac{2}{\mu ^{2}}-\left( {\delta ^{2}+\frac{2}{\mu }\delta +\frac{2}{\mu ^{2}}} \right)e^{-\mu \delta }} \right) \end{aligned}$$

(B2)

and

$$\begin{aligned} \text{ D}_{b}&= \sum \limits _{{i}=0}^{\Delta -1} \int \limits _{{iQ}_{e} }^{{iQ}_{ e} +{Q}_{ e}} \left( {\text{ y}-\text{ iQ}_{e} } \right)^{2}\cdot \mu \text{ e}^{-\mu {y}}\text{ dy}\nonumber \\&= \sum \limits _{{i}=0}^{\Delta -1} \int \limits _{{iQ}_{e} }^{{iQ}_{e} +{Q}_{e} } \left( {\text{ y}-\text{ iQ}_{e} } \right)^{2}\cdot \mu \text{ e}^{-\mu \left( {{y}-{iQ}_{e} +{iQ}_{e} } \right)}\text{ dy} \nonumber \\&= \sum \limits _{{i}=0}^{\Delta -1} \text{ e}^{-\mu {iQ}_{e} }\int \limits _0^{{Q}_{e} } \text{ y}^{{\prime }2}\cdot \mu \text{ e}^{-\mu { y}^{\prime }}\text{ dy}^{\prime }\nonumber \\&= \frac{1-\text{ e}^{-\mu \Delta { Q}_{e} }}{1-\text{ e}^{-\mu {Q}_{e}}}\cdot \left( {\frac{2}{\mu ^{2}}-\left( {\text{ Q}_{e} ^{2}+\frac{2}{\mu }\text{ Q}_{e} +\frac{2}{\mu ^{2}}} \right)\text{ e}^{-\mu {Q}_{e} }} \right)\nonumber \\ \end{aligned}$$

(B3)

Putting (30) and (31) into (29), we can get the distortion model defined in (21).