Skip to main content

Advertisement

Springer Nature Link
Log in

Error-dependent step-size control of adaptive normalized least-mean-square filters used for nonlinear acoustic echo cancellation

  • Original Paper
  • Published:
Signal, Image and Video Processing Aims and scope Submit manuscript

Abstract

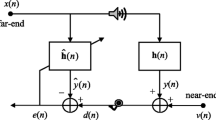
This paper proposes novel acoustic echo cancellation (AEC) approaches based on linear and Volterra structures. The AECs use modified normalized least-mean-square (NLMS) updates to improve the convergence and to maintain the same steady-state misadjustment. In the first case, starting from a new cost function, the resulting variable step size depends on the instant error value and on an estimated error threshold. Secondly, the need of beforehand steady-state error threshold estimation is removed by an automatic step-size control involving the absolute error envelope evolution. The methods are tested for an acoustic enclosure setup modeled using measured linear and quadratic kernels, and their behavior is compared to that of the traditional NLMS and another technique found in the open literature. Also, they are tested for a change in the echo path and for assorted nonlinearity and local signal powers. The comparison is made in terms of the echo-return loss enhancement for WGN and speech as excitation. The simulations show that the proposed adaptations offer increased convergence rates for the same steady-state error.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8

Similar content being viewed by others

References

  1. Paleologu, C., Benesty, J., Ciochina, S.: Sparse Adaptive Filters for Echo Cancellation. Morgan & Claypool Publishers, UK (2010)

    Google Scholar 

  2. Hänsler, E., Schmidt, G.: Topics in Acoustic Echo and Noise Control. Springer, Berlin (2010)

    Google Scholar 

  3. Pavithra, S., Narasimhan, S.V.: Feedback active noise control based on transform-domain forward-backward LMS predictor. Signal Image Video Process. 8(3), 479–487 (2014)

    Article  Google Scholar 

  4. Pavithra, S., Narasimhan, S.V.: Feedback active noise control based on forward-backward LMS predictor. Signal Image Video Process. 7(6), 1083–1091 (2013)

    Article  Google Scholar 

  5. Narasimhan, S.V., Veena, S.: New unbiased adaptive IIR filter: it’s robust and variable step-size versions and application to active noise control. Signal Image Video Process. 7(1), 197–207 (2013)

    Article  Google Scholar 

  6. Albu, F., Paleologu, C., Ciochina, S.: New variable step size affine projection algorithms. In: Proceedings of the IEEE COMM, pp. 63–66, Bucharest (2012)

  7. Gholami-Boroujeny, S., Eshghi, M.: Active noise control using an adaptive bacterial foraging optimization algorithm. Signal Image Video Process. 8(8), 1507–1516 (2014)

    Article  Google Scholar 

  8. Azpicueta-Ruiz, L.A., Zeller, M., Figueiras-Vidal, A.R., Arenas-Garcia, J., Kellermann, W.: Adaptive combination of Volterra kernels and its application to nonlinear acoustic echo cancellation. IEEE Trans. Acoust. Speech Signal Process. 19(1), 97–110 (2011)

    Google Scholar 

  9. Martin, R., Heute, U., Antweiler, C.: Advances in Digital Speech Transmission. Wiley, New York (2008)

    Book  Google Scholar 

  10. Stenger, A., Trautmann, L., Rabenstein, R.: Nonlinear acoustic echo cancellation with second order adaptive Volterra filters. IEEE Trans. Acoust. Speech Signal Process. 2, 877–880 (1999)

    Google Scholar 

  11. Fernandes, C.A.R., Favier, G., Mota, J.C.M.: Decision directed adaptive blind equalization based on the constant modulus algorithm. Signal Image Video Process. 1(4), 333–346 (2007)

    Article  MATH  Google Scholar 

  12. Letexier, D., Bourennane, S., Blanc-Talon, J.: Main flattening directions and Quadtree decomposition for multi-way Wiener filtering. Signal Image Video Process. 1(3), 253–265 (2007)

    Article  MATH  Google Scholar 

  13. Ogunfunmi, T.: Adaptive Nonlinear System Identification: The Volterra and Wiener Model Approaches. Springer, Berlin (2007)

    Book  Google Scholar 

  14. Eweda, E., Zerguine, A.: New insights into the normalization of the least mean fourth algorithm. Signal Image Video Process. 7(2), 255–262 (2013)

    Article  Google Scholar 

  15. Rastegarnia, A., Tinati, M.A., Khalili, A.: Steady-state analysis of quantized distributed incremental LMS algorithm without Gaussian restriction. Signal Image Video Process. 7(2), 227–234 (2013)

    Article  Google Scholar 

  16. Pinchas, M.: What are the analytical conditions for which a blind equalizer will loose the convergence state? Signal Image Video Process. 6(2), 325–340 (2012)

    Article  Google Scholar 

  17. Aboulnasr, T., Mayyas, K.: A robust variable step-size LMS-type algorithm: analysis and simulations. IEEE Trans. Signal Process. 45(3), 631–639 (1997)

    Article  Google Scholar 

  18. Kwong, R.H., Johnston, E.W.: A variable step size LMS algorithm. IEEE Trans. Signal Process. 40, 1633–1642 (1992)

    Article  MATH  Google Scholar 

  19. Widrow, B., McCool, J.M., Larimore, M., Johnson, C.R.: Stationary and nonstationary learning characteristics of the LMS adaptive filter. Proc. IEEE 64, 1151–1162 (1976)

    Article  MathSciNet  Google Scholar 

  20. Mathews, V.J., Xie, Z.: A stochastic gradient adaptive filter with gradient adaptive step size. IEEE Trans. Signal Process. 41, 2075–2087 (1993)

    Article  Google Scholar 

  21. Shih, C.-S., Hsieh, S.-F.: Fast converging nonlinear echo cancellation based on optimum step size. In: IEEE International Symposium on Signal Processing and Information Technology (ISSPIT), pp. 135–139 (2009)

  22. Kuech, F., Kellermann, W.: Coefficient-dependent step-size for adaptive second-order Volterra filters. EUSIPCO, Vienna (2004)

    Google Scholar 

  23. Rusu, C., Cowan, C.F.N.: The exponentiated convex variable step-size (ECVSS) algorithm. Signal Process. 90, 2784–2791 (2010)

    Article  MATH  Google Scholar 

  24. Contan, C., Kirei, B.S., Topa, M.D.: Modified NLMF adaptation of Volterra filters used for nonlinear acoustic echo cancellation. Signal Process. 93, 1152–1161 (2013)

    Article  Google Scholar 

  25. Sayed, A.H.: Fundamentals of Adaptive Filtering. Wiley, University of California, Los Angeles (2003)

    Google Scholar 

  26. Chan, S.C., Zhou, Y.: Convergence behavior of NLMS algorithm for Gaussian inputs: solutions using generalized abelian integral functions and step size selection. J. Signal Process. Syst. 59(3), 255–265 (2010)

    Article  Google Scholar 

  27. Kuech, F., Kellermann, W.: Orthogonalized power filters for nonlinear acoustic echo cancellation. Signal Process. 86(6), 1168–1181 (2006)

    Article  MATH  Google Scholar 

Download references

Acknowledgments

The authors thank Prof. Dr.-Ing. Walter Kellermann and Dr.-Ing. Marcus Zeller from the University of Erlangen-Nuremberg, Germany, for providing measured kernels for experiments. This paper was supported by the Post-Doctoral Programme POSDRU/159/1.5/S/137516, project co-funded from European Social Fund through the Human Resources Sectorial Operational Program 2007–2013.

Author information

Authors and Affiliations

  1. Bases of Electronics Department, Technical University of Cluj-Napoca, Cluj-Napoca, Romania

    Cristian Contan, Botond Sandor Kirei & Marina Dana Topa

Authors
  1. Cristian Contan
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Botond Sandor Kirei
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Marina Dana Topa
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Cristian Contan.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Contan, C., Kirei, B.S. & Topa, M.D. Error-dependent step-size control of adaptive normalized least-mean-square filters used for nonlinear acoustic echo cancellation. SIViP 10, 511–518 (2016). https://doi.org/10.1007/s11760-015-0769-1

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11760-015-0769-1

Keywords