Skip to main content
Springer Nature Link
Log in

Blind multi-image super-resolution based on combination of ANN learning and non-subsampled Contourlet directional image representation

  • Original Paper
  • Published:
Signal, Image and Video Processing Aims and scope Submit manuscript

Abstract

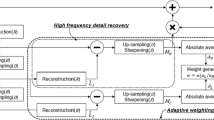
In image super-resolution technique, it is contradictory to keep the edge characteristics of the image while de-noising. In order to solve the above problem, we propose a blind multi-image super-resolution algorithm which is adaptive to the image content and does not need the fuzzy conditions of generating the low-resolution images. The initially estimated high-resolution image \(\left( \hat{H}\right) \) is firstly gotten through the traditional reconstruction algorithm. Afterward, the estimation differences of low-resolution images are utilized as the input of artificial neural network (ANN), and the band-pass directional sub-bands of non-subsampled Contourlet transform (NSCT) of the lost high-frequency components are outputted in ANN. With the inverse NSCT, we can get the estimated lost high-frequency components. Finally, the estimated lost high-frequency components and the adaptive weighted matrix generated from the image content are multiplied before being added to \(\hat{H}\). Experimental results show that the high-resolution images obtained through the proposed method can achieve favorable subjective and objective quality for different image contents. Meantime, it is superior to some of the state-of-the-art classical methods in terms of the performance.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8

Similar content being viewed by others

References

  1. Yao, P., Xue, J.X., Dai, G.Z.: An overview on super-resolution images processing. Bandaoti Guangdian/Semicond. Optoelection. 30(4), 492–497 (2009)

    Google Scholar 

  2. Zhou, Y., Tang, Z., Hu, X.: Fast single image super resolution reconstruction via image separation. J. Netw. 9(7), 1811–1818 (2014)

    Google Scholar 

  3. Xiong, Z., Xu, D., Sun, X., et al.: Example-based super-resolution with soft information and decision. IEEE Trans. Multimed. 15(6), 1458–1465 (2013)

    Article  Google Scholar 

  4. Kim, W.H., Lee, J.S.: Blind single image super resolution with low computational complexity. Multimed. Tools Appl. (2016). doi:10.1007/s11042-016-3396-0

    Google Scholar 

  5. Anver, J., Abdulla, P.: Single-image super-resolution using kernel recursive least squares. Signal Image Video Process. 10(8), 1–8 (2016)

    Article  Google Scholar 

  6. Cha, Y., Kim, S.: Edge-forming methods for color image zooming. IEEE Trans. Image Process. 15(8), 2315–2323 (2006)

    Article  Google Scholar 

  7. Stark, H., Oskoui, P.: High resolution image recovery from image-plane arrays, using convex projections. J. Opt. Soc. Am. A 6(11), 1715–1726 (1989)

    Article  Google Scholar 

  8. Irani, M., Peleg, S.: Improving resolution by image registration. Comput. Vis. Graph. Image Process. Graph. Models Image Process. 53, 231–239 (1991)

    Google Scholar 

  9. Schulz, R.R., Stevenson, R.L.: A Bayesian approach to image expansion for improved definition. IEEE Trans. Image Process. 3(3), 233–242 (1994)

    Article  Google Scholar 

  10. Nguyen, N., Milanfar, P., Golub, G.: A computationally efficient superresolution image reconstruction algorithm. IEEE Trans. Image Process. 10(4), 573–583 (2001)

    Article  MATH  Google Scholar 

  11. Dong, W., Zhang, D., Shi, G., et al.: Image deblurring and super-resolution by adaptive sparse domain selection and adaptive regularization. IEEE Trans. Image Process. 20(7), 1838–1857 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  12. Maiseli, B.J., Elisha, O.A., Gao, H.: A multi-frame super-resolution method based on the variable-exponent nonlinear diffusion regularizer. Eurasip J. Image Video Process. 2015(1), 1–16 (2015)

    Article  Google Scholar 

  13. Ren, Z., He, C., Zhang, Q.: Fractional order total variation regularization for image super-resolution. Signal Process. 93(9), 2408–2421 (2013)

    Article  Google Scholar 

  14. Tsai, R.Y., Huang, T.S.: Multiple frame image restoration and registration. In: Huang, T. S Advances in Computer Vision and Image Processing, pp. 317–339. JAI Press, Greenwich (1984)

  15. Kim, S.P., Su, W.Y.: Recursive high-resolution reconstruction of blurred multi-frame images. IEEE Trans. Image Process. 2(4), 534–539 (1993)

    Article  Google Scholar 

  16. Rhee, S.H., Kang, M.G.: Discrete cosine transform-based regularized high-resolution image reconstruction algorithm. Opt. Eng. 38(8), 1348–1356 (1999)

    Article  Google Scholar 

  17. Vandewalle, P., Ssstrunk, S., Vetterli, M.: A frequency domain approach to registration of aliased images with application to super-resolution. Eurasip J. Appl. Signal Process. 2006(1), 1–14 (2006). (Special issue on super-resolution)

    Google Scholar 

  18. Shin, D.K., Moon, Y.S.: Super-resolution image reconstruction using wavelet based patch and discrete wavelet transform. J. Signal Process. Syst. 81(1), 71–81 (2015)

    Article  Google Scholar 

  19. Suryanarayana, G., Dhuli, R.: Shock filter based image super-resolution using dual-tree complex wavelet transform and singular value decomposition. Int. J. Comput. Math. Electr. Electron. Eng. 35(3), 1162–1178 (2016)

    Article  Google Scholar 

  20. Shah, A.J., Makwana, R., Gupta, S.B.: Single image super-resolution via non sub-sample Contourlet transform based learning and a Gabor prior. Int. J. Comput. Appl. 64(18), 32–38 (2013)

    Google Scholar 

  21. Kumar, N., Sethi, A.: Fast learning-based single image super-resolution. IEEE Trans. Multimed. 18(8), 1504–1515 (2016)

    Article  Google Scholar 

  22. Li, J., Wu, J., Deng, H.P., et al.: A self-learning image super-resolution method via sparse representation and non-local similarity. Neurocomputing 184, 196–206 (2016)

    Article  Google Scholar 

  23. Shah, A.J., Gupta, S.B.: Adaptive directional decomposition in non sub sample Contourlet transform domain for single image super resolution. Multimed. Tools Appl. 75(14), 8443–8467 (2016)

    Article  Google Scholar 

  24. Da, C.A., Zhou, J., Do, M.N.: The nonsubsampled Contourlet transform: theory, design, and applications. IEEE Trans. Image Process. 15(10), 3089–3101 (2006)

    Article  Google Scholar 

  25. Selvi, G.U.V., Nadarajan, R.: CT and MRI image compression using wavelet-based Contourlet transform and binary array technique. J. Real-Time Image Proc. (2014). doi:10.1007/s11554-014-0400-7

    Google Scholar 

  26. Yan, C., Zhang, K., Qi, Y.: Image denoising using modified nonsubsampled Contourlet transform combined with Gaussian scale mixtures model. In: Intelligence Science and Big Data Engineering. Image and Video Data Engineering, LNCS 9242, pp. 196–207. Springer, Amsterdam (2015)

  27. Sonwane, M.K.R., Chuhan, M.B.: Multimodality image fusion by using activity level measurement and counterlet transform. Int. J. Recent Innov. Trends Comput. Commun. 2(3), 612–616 (2014)

    Google Scholar 

  28. Verma, S., Gupta, H.: Comparative result analysis of novel algorithm based on RBF network for image enhancement. Int. J. Adv. Comput. Res. 3(10), 17–23 (2013)

    Google Scholar 

  29. Saito, Y., Osana, Y.: Identification of artifacts in scenery images using color and line information by RBF network and k-means. Antimicrob. Agents Chemother. 57(8), 1065–1072 (2009)

    Google Scholar 

  30. Wang, Z., Bovik, A.C., Sheikh, H.R., et al.: Image quality assessment: from error visibility to structural similarity. IEEE Trans. Image Process. 13(4), 600–612 (2004)

    Article  Google Scholar 

  31. Panda, S.S., Prasad, M.S.R.S., Jena, G.: POCS based super-resolution image reconstruction using an adaptive regularization parameter. Int. J. Comput. Sci. Issues 8(5), 155–158 (2011)

    Google Scholar 

  32. Maiseli, B.J., Liu, Q., Elisha, O.A., et al.: Adaptive Charbonnier super-resolution method with robust edge preservation capabilities. J. Electron. Imaging 22(22), 451–459 (2013)

    Google Scholar 

  33. ITU Study Group 12: Series P: telephone transmission quality (methods for objective and subjective assessment of quality) methods for subjective determination of transmission quality. ITU-T P.800 (1996)

Download references

Acknowledgements

This work was jointly supported by the National Natural Science Foundation of China (No. 61201347), Chongqing Foundation and Advanced Research Project (No. cstc2016jcyjA0103), the Natural Science Foundation Project of CQ CSTC (No. cstc2012jjA40011), and the Fundamental Research Funds for the Central Universities (No. CDJZR13185502). The support is gratefully acknowledged.

Author information

Authors and Affiliations

  1. College of Communication Engineering, Chongqing University, Chongqing, China

    Zhiyong Shi, Fengchun Tian & Jian Ran

  2. Chongqing Communication Institute, Chongqing, China

    Zhiyong Shi & Yande Wang

Authors
  1. Zhiyong Shi
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Fengchun Tian
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Yande Wang
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. Jian Ran
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Fengchun Tian.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Shi, Z., Tian, F., Wang, Y. et al. Blind multi-image super-resolution based on combination of ANN learning and non-subsampled Contourlet directional image representation. SIViP 12, 25–31 (2018). https://doi.org/10.1007/s11760-017-1126-3

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11760-017-1126-3

Keywords