Skip to main content

Advertisement

SpringerLink
Log in

Parameter estimation for Hammerstein control autoregressive systems using differential evolution

  • Original Paper
  • Published:
Signal, Image and Video Processing Aims and scope Submit manuscript

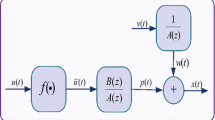
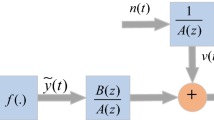
Abstract

In the present study, strength of stochastic computational paradigms is investigated for parameter estimation of Hammerstein control autoregressive (HCAR) model by exploiting differential evolution, genetic algorithms and pattern search methods. Multidimensional and nonlinear nature of the problem emerging in digital signal systems along with noise makes it a challenging optimization task, which is dealt with robustness and effectiveness of stochastic solvers to ensure convergence and avoid trapping in local minima. The performance of meta-heuristic approaches is validated through statistical performance indices based on absolute error, weight deviations and mean squared error. Comparative studies of HCAR system identification established efficacy of the designed methodology based on differential evolution over its counterparts.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4

Similar content being viewed by others

References

  1. Djurović, I.: Estimation of sinusoidal frequency-modulated signal parameters in high-noise environment. Signal Image Video Process. 11(8), 1537–1541 (2017)

    Article  Google Scholar 

  2. Ma, W., Chen, B., Qu, H., Zhao, J.: Sparse least mean p-power algorithms for channel estimation in the presence of impulsive noise. Signal Image Video Process. 10(3), 503–510 (2016)

    Article  Google Scholar 

  3. Djurović, I.: QML-RANSAC: PPS and FM signals estimation in heavy noise environments. Signal Process. 130, 142–151 (2017)

    Article  Google Scholar 

  4. Li, L.: Joint parameter estimation and target localization for bistatic MIMO radar system in impulsive noise. Signal Image Video Process. 9(8), 1775–1783 (2015)

    Article  Google Scholar 

  5. Yang, P., Liu, Z., Jiang, W.L.: Parameter estimation of multi-component chirp signals based on discrete chirp Fourier transform and population Monte Carlo. Signal Image Video Process. 9(5), 1137–1149 (2015)

    Article  Google Scholar 

  6. Sudeep, P.V., Palanisamy, P., Kesavadas, C., Sijbers, J., Arnold, J., Rajan, J.: A nonlocal maximum likelihood estimation method for enhancing magnetic resonance phase maps. Signal Image Video Process. 11(5), 913–920 (2017)

    Article  Google Scholar 

  7. Bey, N.Y.: Highly accurate frequency estimation of brief duration signals in noise. Signal Image Video Process. (2018). https://doi.org/10.1007/s11760-018-1280-2

    Google Scholar 

  8. Ma, W., Zheng, D., Zhang, Z., Duan, J., Chen, B.: Robust proportionate adaptive filter based on maximum correntropy criterion for sparse system identification in impulsive noise environments. Signal Image Video Process. 12(1), 117–124 (2018)

    Article  Google Scholar 

  9. Bai, E.W. (ed.): Block-Oriented Nonlinear System Identification, vol. 1. Springer, London (2010)

    MATH  Google Scholar 

  10. Billings, S.A.: Nonlinear system identification: NARMAX methods in the time, frequency, and spatio-temporal domains. Wiley, London (2013)

    Book  MATH  Google Scholar 

  11. Ding, F., Liu, X., Liu, M.: The recursive least squares identification algorithm for a class of Wiener nonlinear systems. J. Frankl. Inst. 353(7), 1518–1526 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  12. Pal, P.S., Kar, R., Mandal, D., Ghoshal, S.P.: A hybrid backtracking search algorithm with wavelet mutation-based nonlinear system identification of Hammerstein models. Signal Image Video Process. 11(5), 929–936 (2017)

    Article  Google Scholar 

  13. Tang, Y., Bu, C., Liu, M., Zhang, L., Lian, Q.: Application of ELM-Hammerstein model to the identification of solid oxide fuel cells. Neural Comput. Appl. 29(2), 401–411 (2018)

    Article  Google Scholar 

  14. Zhang, Q., Wang, Q., Li, G.: Nonlinear modeling and predictive functional control of Hammerstein system with application to the turntable servo system. Mech. Syst. Signal Process. 72, 383–394 (2016)

    Article  Google Scholar 

  15. Togun, N., Baysec, S.: Nonlinear identification of a spark ignition engine torque based on NFIS with NARX method. Expert Syst. 33(6), 559–568 (2016)

    Article  Google Scholar 

  16. Ávila, F.R., Carvalho, H.T., Biscainho, L.W.: Bayesian blind identification of nonlinear distortion with memory for audio applications. IEEE Signal Process. Lett. 23(4), 414–418 (2016)

    Article  Google Scholar 

  17. Chagtmi, N., Boulejfen, N., Ghannouchi, F.M.: Augmented Hammerstein model for six-port-based wireless receiver calibration. IET Commun. 11(6), 951–960 (2017)

    Article  Google Scholar 

  18. Cornejo-Aragón, L.G., Santos-Cuevas, C.L., Ocampo-García, B.E., Chairez-Oria, I., Diaz-Nieto, L., García-Quiroz, J.: Preclinical biokinetic modelling of Tc-99m radiophamaceuticals obtained from Semi-Automatic image processing. J. Med. Biol. Eng. 37(6), 887–898 (2017)

    Article  Google Scholar 

  19. Ding, F., Wang, X., Mao, L., Xu, L.: Joint state and multi-innovation parameter estimation for time-delay linear systems and its convergence based on the Kalman filtering. Digit. Signal Process. 62, 211–223 (2017)

    Article  Google Scholar 

  20. Li, M., Liu, X.: The least squares based iterative algorithms for parameter estimation of a bilinear system with autoregressive noise using the data filtering technique. Signal Process. 147, 23–34 (2018)

    Article  Google Scholar 

  21. Chen, M., Ding, F., Xu, L., Hayat, T., Alsaedi, A.: Iterative identification algorithms for bilinear-in-parameter systems with autoregressive moving average noise. J. Frankl. Inst. 354(17), 7885–7898 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  22. Zhang, X., Ding, F., Alsaadi, F.E., Hayat, T.: Recursive parameter identification of the dynamical models for bilinear state space systems. Nonlinear Dyn. 89(4), 2415–2429 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  23. Ding, F., Wang, X.: Hierarchical stochastic gradient algorithm and its performance analysis for a class of bilinear-in-parameter systems. Circuits Syst. Signal Process. 36(4), 1393–1405 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  24. Ding, F., Wang, Y., Dai, J., Li, Q., Chen, Q.: A recursive least squares parameter estimation algorithm for output nonlinear autoregressive systems using the input-output data filtering. J. Frankl. Inst. 354(15), 6938–6955 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  25. Ding, F., Deng, K., Liu, X.: Decomposition based Newton iterative identification method for a Hammerstein nonlinear FIR system with ARMA noise. Circuits Syst. Signal Process. 33(9), 2881–2893 (2014)

    Article  MathSciNet  Google Scholar 

  26. Mao, Y., Ding, F.: A novel parameter separation based identification algorithm for Hammerstein systems. Appl. Math. Lett. 60, 21–27 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  27. Ding, F., Liu, X., Chu, J.: Gradient-based and least-squares-based iterative algorithms for Hammerstein systems using the hierarchical identification principle. IET Control Theory Appl. 7(2), 176–184 (2013)

    Article  MathSciNet  Google Scholar 

  28. Wang, D.: Hierarchical parameter estimation for a class of MIMO Hammerstein systems based on the reframed models. Appl. Math. Lett. 57, 13–19 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  29. Ding, F.: Hierarchical multi-innovation stochastic gradient algorithm for Hammerstein nonlinear system modeling. Appl. Math. Model. 37(4), 1694–1704 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  30. Shen, Q., Ding, F.: Hierarchical multi-innovation extended stochastic gradient algorithms for input nonlinear multivariable OEMA systems by the key-term separation principle. Nonlinear Dyn. 85(1), 499–507 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  31. Mao, Y., Ding, F., Yang, E.: Adaptive filtering-based multi-innovation gradient algorithm for input nonlinear systems with autoregressive noise. Int. J Adapt. Control Signal Process. 31(10), 1388–1400 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  32. Mao, Y., Ding, F.: Data filtering-based multi-innovation stochastic gradient algorithm for nonlinear output error autoregressive systems. Circuits Syst. Signal Process. 35(2), 651–667 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  33. Chaudhary, N.I., Raja, M.A.Z.: Identification of Hammerstein nonlinear ARMAX systems using nonlinear adaptive algorithms. Nonlinear Dyn. 79(2), 1385–1397 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  34. Chaudhary, N.I., Raja, M.A.Z., Khan, A.U.R.: Design of modified fractional adaptive strategies for Hammerstein nonlinear control autoregressive systems. Nonlinear Dyn. 82(4), 1811–1830 (2015)

    Article  Google Scholar 

  35. Chaudhary, N.I., Raja, M.A.Z.: Design of fractional adaptive strategy for input nonlinear Box-Jenkins systems. Signal Process. 116, 141–151 (2015)

    Article  Google Scholar 

  36. Aslam, M.S., Chaudhary, N.I., Raja, M.A.Z.: A sliding-window approximation-based fractional adaptive strategy for Hammerstein nonlinear ARMAX systems. Nonlinear Dyn. 87(1), 519–533 (2017)

    Article  MATH  Google Scholar 

  37. Chaudhary, N.I., Aslam, M.S., Raja, M.A.Z.: Modified Volterra LMS algorithm to fractional order for identification of Hammerstein non-linear system. IET Signal Process. 11(8), 975–985 (2017)

    Article  Google Scholar 

  38. Raja, M.A.Z., Shah, F.H., Khan, A.A., Khan, N.A.: Design of bio-inspired computational intelligence technique for solving steady thin film flow of Johnson-Segalman fluid on vertical cylinder for drainage problems. J. Taiwan Inst. Chem. Eng. 60, 59–75 (2016)

    Article  Google Scholar 

  39. Arqub, O.A., Abo-Hammour, Z.: Numerical solution of systems of second-order boundary value problems using continuous genetic algorithm. Inf. Sci. 279, 396–415 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  40. Raja, M.A.Z., Mehmood, A., Niazi, S.A., Shah, S.M.: Computational intelligence methodology for the analysis of RC circuit modelled with nonlinear differential order system. Neural Comput. Appl. (2016). https://doi.org/10.1007/s00521-016-2806-6

    Google Scholar 

  41. Raja, M.A.Z., Shah, F.H., Alaidarous, E.S., Syam, M.I.: Design of bio-inspired heuristic technique integrated with interior-point algorithm to analyze the dynamics of heartbeat model. Appl. Soft Comput. 52, 605–629 (2017)

    Article  Google Scholar 

  42. Raja, M.A.Z., Manzar, M.A., Shah, F.H., Shah, F.H.: Intelligent computing for Mathieu’s systems for parameter excitation, vertically driven pendulum and dusty plasma models. Appl. Soft Comput. 62, 359–372 (2017)

    Article  Google Scholar 

  43. Cárdenas-Montes, M., Vega-Rodríguez, M., Molla, M.: Modeling low-resolution galaxy spectral energy distribution with evolutionary algorithms. Neurocomputing (2017). https://doi.org/10.1016/j.neucom.2017.01.125

    Google Scholar 

  44. Raja, M.A.Z., Shah, A.A., Mehmood, A., Chaudhary, N.I., Aslam, M.S.: Bio-inspired computational heuristics for parameter estimation of nonlinear Hammerstein controlled autoregressive system. Neural Comput. Appl. (2016). https://doi.org/10.1007/s00521-016-2677-x

    Google Scholar 

  45. Guedes, J., Castoldi, M., Goedtel, A., Agulhari, C., Sanches, D.: Parameters estimation of three-phase induction motors using differential evolution. Electr. Power Syst. Res. 154, 204–212 (2017)

    Article  Google Scholar 

  46. Storn, R., Price, K.: Differential evolution—a simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 11(4), 341–359 (1997)

    Article  MathSciNet  MATH  Google Scholar 

  47. Price, K., Storn, R.M., Lampinen, J.A.: Differential Evolution: A Practical Approach to Global Optimization. Springer, Berlin (2006)

    MATH  Google Scholar 

  48. Goldberg, D.E., Holland, J.H.: Genetic algorithms and machine learning. Mach. Learn. 3(2), 95–99 (1988)

    Article  Google Scholar 

  49. Gen, M., Cheng, R.: Genetic Algorithms and Engineering Optimization, vol. 7. Wiley, London (2000)

    Google Scholar 

  50. Kolda, T.G., Lewis, R.M., Torczon, V.: Optimization by direct search: new perspectives on some classical and modern methods. SIAM Rev. 45(3), 385–482 (2003)

    Article  MathSciNet  MATH  Google Scholar 

  51. Song, X., Gu, H., Zhang, X., Liu, J.: Pattern search algorithms for nonlinear inversion of high-frequency Rayleigh-wave dispersion curves. Comput. Geosci. 34(6), 611–624 (2008)

    Article  Google Scholar 

  52. Arqub, O.A., Mohammed, A.S., Momani, S., Hayat, T.: Numerical solutions of fuzzy differential equations using reproducing kernel Hilbert space method. Soft Comput. 20(8), 3283–3302 (2016)

    Article  MATH  Google Scholar 

  53. Arqub, O.A., Al-Smadi, M., Momani, S., Hayat, T.: Application of reproducing kernel algorithm for solving second-order, two-point fuzzy boundary value problems. Soft Comput. 21(23), 7191–7206 (2017)

    Article  MATH  Google Scholar 

  54. Arqub, O.A.: Adaptation of reproducing kernel algorithm for solving fuzzy Fredholm-Volterra integrodifferential equations. Neural Comput. Appl. 28(7), 1591–1610 (2017)

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Electrical Engineering, Pakistan Institute of Engineering and Applied Sciences, Nilore, Islamabad, Pakistan

    Ammara Mehmood

  2. School of Electrical and Electronic Engineering, University of Adelaide, Adelaide, Australia

    Muhammad Saeed Aslam

  3. Department of Electrical Engineering, International Islamic University, Islamabad, Pakistan

    Naveed Ishtiaq Chaudhary

  4. Department of Computer and Information Sciences, Pakistan Institute of Engineering and Applied Sciences, Nilore, Islamabad, Pakistan

    Aneela Zameer

  5. Department of Electrical Engineering, COMSATS Institute of Information Technology, Attock, Pakistan

    Muhammad Asif Zahoor Raja

Authors
  1. Ammara Mehmood
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Muhammad Saeed Aslam
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Naveed Ishtiaq Chaudhary
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Aneela Zameer
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Muhammad Asif Zahoor Raja
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Muhammad Saeed Aslam.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Mehmood, A., Aslam, M.S., Chaudhary, N.I. et al. Parameter estimation for Hammerstein control autoregressive systems using differential evolution. SIViP 12, 1603–1610 (2018). https://doi.org/10.1007/s11760-018-1317-6

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11760-018-1317-6

Keywords

Search

Navigation