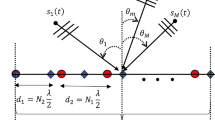
Abstract
The direction-finding (DF) problem for unfolded co-prime linear array (UCLA) is researched. Specifically, there is a need to address the critical issue of non-trivial ambiguity in estimating the angle-of-arrival (AOA) parameter. To address this issue, an improved polynomial rooting-based method is proposed. A polynomial function is derived based on the orthogonality between the noise subspace singular vectors and array response vectors. In order to select the signal roots that are related to true AOAs over ambiguous roots, a maximum signal power function is proposed based on spatial filtering and second-order differential. The proposed method overcomes the non-trivial ambiguity and estimates the true AOAs successfully with improved estimation performances in terms of reliability, accuracy and angular resolution involving low computational cost. Simulations have been performed to show the effectiveness and superiority of the proposed method.






Similar content being viewed by others
References
Shu, F., Shen, T., Xu, L., Qin, Y., Wan, S., Jin, S., You, X., Wang, J.: Directional modulation: a physical-layer security solution to B5G and future wireless networks. IEEE Network 34(2), 210–216 (2020)
Liao, B., Madanayake, A., Agathaklis, P.: Array signal processing and systems. Multidimens. Syst. Sign. Process. 29(2), 467–473 (2018)
Grenier, D., Elahian, B., Blanchard-Lapierre, A.: Joint delay and direction of arrivals estimation in mobile communications. Signal Image Video Process. 10(1), 45–54 (2016)
Tokgoz, S., Panahi, I.M.S.: Robust three-microphone speech source localization using randomized singular value decomposition. IEEE Access. 9, 157800–157811 (2021)
Dehghan Firoozabadi, A., Irarrazaval, P., Adasme, P., et al.: A novel method for estimating the number of speakers based on generalized eigenvalue–vector decomposition and adaptive wavelet transform by using K-means clustering. Signal Image Video Process. 14, 1017–1025 (2020)
Tuncer, T.E., Friedlander, B.: Classical and Modern Direction-of-Arrival Estimation. Academic Press, London (2009)
Moffet, A.T.: Minimum-redundancy linear arrays. IEEE Trans. Antennas Propag. 16(2), 172–175 (1968)
Vertatschitsch, E., Haykin, S.: Nonredundant arrays. Proc. IEEE. 74(1), 217 (1986)
Pal, P., Vaidyanathan, P.P.: Nested arrays: A novel approach to array processing with enhanced degrees of freedom. IEEE Trans. Signal Proc. 58(8), 4167–4181 (2010)
Vaidyanathan, P.P., Pal, P.: Sparse sensing with co-prime samplers and arrays. IEEE Trans. Signal Proc. 59(2), 573–586 (2011)
Tan, Z., Eldar, Y., Nehorai, A.: Direction of arrival estimation using co-prime arrays: a super-resolution viewpoint. IEEE Trans. Signal Proc. 62(21), 5565–5576 (2014)
Qin, S., Zhang, Y., Amin, M.: Generalized coprime array configurations for direction-of-arrival estimation. IEEE Trans. Signal Proc. 63(6), 1377–1390 (2015)
Liu, C.-L., Vaidyanathan, P.P.: Remarks on the spatial smoothing step in coarray MUSIC. IEEE Signal Process. Lett. 22(9), 1438–1442 (2015)
Xie, Q., Pan, X., Xiao, S.: Enhance degrees of freedom for coprime array using optspace algorithm. IEEE Access. 7, 32672–32680 (2019)
Yang, X., Wang, Y., Chargé, P., Ding, Y.: An efficient DOA estimation method for co-prime linear arrays. IEEE Access. 7, 90874–90881 (2019)
Zhou, C., Shi, Z., Gu, Y., Shen, X.: DECOM: DOA estimation with combined MUSIC for coprime array. In: IEEE international conference on wireless communication signal processing. pp. 1–5 (2013)
Sun, F.G., Lan, P., Gao, B.: Partial spectral search-based DOA estimation method for co-prime linear arrays. Electron. Lett. 51(24), 2053–2055 (2015)
Sun, F., Gao, B., Chen, L., Lan, P.: A low-complexity ESPRIT-based DOA estimation method for co-prime linear arrays. Sensors. 16(9), 1367 (2016)
Zhang, D., Zhang, Y., Zheng, G., Feng, C., Tang, J.: Improved DOA estimation algorithm for co-prime linear arrays using root-MUSIC algorithm. Electron. Lett. 53(18), 1277–1279 (2017)
Yan, F., Liu, S., Wang, J., Jin, M., Shen, Y.: Fast DOA estimation using co-prime array. Electron. Lett. 54(7), 409–410 (2018)
Liu, A., Yang, Q., Zhang, X., Deng, W.: Modified root music for co-prime linear arrays. Electron. Lett. 54(15), 949–951 (2018)
Zheng, W., Zhang, X., Gong, P., Zhai, H.: DOA estimation for coprime linear array: an ambiguity-free method involving full DOFs. IEEE Commun. Lett. 22(3), 562–565 (2018)
He, W., Yang, X., Wang, Y.: A high-resolution and low-complexity DOA estimation method with unfolded coprime linear arrays. Sensors. 20(1), 218 (2020)
Liu, J., Zhao, Z., He, Z., Nie, Z., Liu, Q.: Resolving manifold ambiguities for direction-of-arrival estimation of sparse array using semi-circular substrates. IET Microwaves Antennas Propag. 7(12), 1016–1020 (2013)
Yang, X., Wang, Y., Chargé, P.: Modified DOA estimation with an unfolded co-prime linear array. IEEE Commun. Lett. 23(5), 859–862 (2019)
Huang, X., Yang, X., Cao, L., Lu, W.: Pseudo noise subspace based DOA estimation for unfolded coprime linear arrays. IEEE Commun. Lett. 10(11), 2335–2339 (2021)
Manikas, A.: Differential Geometry in Array Processing. Imperial College Press, London (2004)
Stoica, P., Nehorai, A.: Performance study of conditional and unconditional direction-of-arrival estimation. IEEE Trans. Acoust. Speech Signal Process. 38(10), 1783–1795 (1990)
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Ashok, C., Venkateswaran, N. An improved polynomial rooting-based method for solving non-trivial ambiguity in direction-finding using an unfolded co-prime linear array. SIViP 17, 219–226 (2023). https://doi.org/10.1007/s11760-022-02224-0
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11760-022-02224-0