Abstract
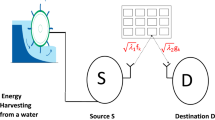
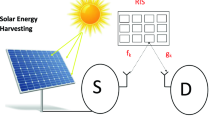
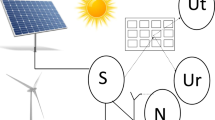
Simultaneously Transmitting and Reflecting Reconfigurable Intelligent Surfaces (STAR-RIS) represent a cutting-edge technology in wireless communications, allowing surfaces to both transmit and reflect signals simultaneously. This dual functionality provides greater flexibility and efficiency in signal propagation and spectrum management. Integrating energy harvesting from vibrations into STAR-RIS creates an innovative and sustainable solution for powering these systems, enabling autonomous operation in environments where conventional power sources are unavailable. By converting ambient mechanical energy into electrical power, vibration-based energy harvesting supports the continuous operation of STAR-RIS without reliance on external energy sources. This advancement has significant implications for the deployment of future wireless networks, including smart cities, the Internet of Things, and remote sensing applications, offering a pathway to greener and more efficient communication infrastructure.








Similar content being viewed by others
Data availibility
Material and data are not available.
References
Mu, X., Liu, Y., Xu, J., Guo, L., Lin, J.: Joint Beamforming Optimization for Simultaneously Transmitting And Reflecting (STAR) RIS Aided Communications, (Invited Paper), 2021 55th Asilomar Conference on Signals, Systems, and Computers
Xidong, M., Liu, Y, Guo, L., Lin, J., Schober, R.: Simultaneously transmitting and reflecting (STAR) RIS aided wireless communications. IEEE Transact. Wireless Commun. 21(5) (2022)
Aldababsa, M., Khaleel, A., Basar, E.: STAR-RIS-NOMA networks: an error performance perspective. IEEE Commun. Lett. 26(8) (2022)
Mu, X., Liu, Y., Guo, L., Lin, J., Schober, R.: Simultaneously transmitting and reflecting (STAR) RIS aided wireless communications. IEEE Transact. Wireless Commun. 21(5) (2022)
Kan, J., He, C., Lin, Y., Lin, S., Cao, Z., Zhang, Z.: Low-frequency piezoelectric energy harvesting from coupled longitudinal-transverse vibration of two magnetic coupling-based orthogonal beams. IEEE Sens. J., (2024). Early Access Article
Chen, Zhongsheng, Chen, Zhiwen, Nie, Gaofa, Li, Kaiqiang: “Analytical and Experimental Investigations on Low-Frequency Simultaneous Vibration Isolation and Energy Harvesting Using Magnetic Rings”. IEEE Access (2024), Vol. 12, Early access
Zhao, Sheng, R., Ujwal, L., Jeffrey H.: Impact of duffing and piezoelectric-coupling nonlinearities on piezoelectric vibration energy harvesting. IEEE Sens. J. 24(6) (2024)
Hou, X., Niu, L., Qian, S., Dongxu, H., Hou, J., Shi, S., Geng, W., He, J., Chou, X.: Electromagnetic energy harvester based on bidirectional vibration to unidirectional rotation conversion for environmental low-frequency vibration energy harvesting. IEEE Transact. Power Electron. 39(2) (2024)
Xiao, H., Peng, H., Sun, H., Zhao, Y., Liu, X., Jiang, C.: Automatic impedance matching with dual time-scale P O in fully self-powered electromagnetic vibration energy harvesting. IEEE Transact. Power Electron. 39(3) (2024)
Yoshida, Y., Hiraga, M., Miura, N., Masuda, A.: An Ideal Softening Resonator for Nonlinear Vibration Energy Harvesting with Flat Power Characteristics. 2023 IEEE 22nd International Conference on Micro and Nanotechnology for Power Generation and Energy Conversion Applications (PowerMEMS)
Jia, Y., Arroyo, E., Seshia, A.A.: Optimizing the substrate-to-piezoelectric thickness ratio of micro-fabricated Aln-on-Si vibration energy harvesting’. 2023 IEEE 22nd International Conference on Micro and Nanotechnology for Power Generation and Energy Conversion Applications (PowerMEMS)
Theodossiades, S., Alevras, P.: Concept Designs for Vibration Energy Harvesting Employing Nonlinear Dynamics. 2023 IEEE 22nd International Conference on Micro and Nanotechnology for Power Generation and Energy Conversion Applications (PowerMEMS)
Shabanalinezhad, H., Malcovati, P., Svelto, C., Gatti, G.: Vibration Energy Harvesting from Planar Excitations in Industrial Machines’. 2023 IEEE International Conference on Metrology for eXtended Reality, Artificial Intelligence and Neural Engineering (MetroXRAINE)
Gao, Y., Fu, F., Chen, L., Chen, Q., Wang, Z., Tan, Z., Ni, Y.: Energy Harvesting Analysis and Sensing Application of Cantilever Structure Based on Aeolian Vibration and Piezoelectric Effect”. 2023 IEEE International Conference on Advanced Power System Automation and Protection (APAP)
Despotovic, Ž.V., Petrovic, M.V., Bobic, J.D.: A Realisation of Synchronous Buck Power Converter for Energy Harvesting from Vibrations”. 2023 22nd International Symposium on Power Electronics (Ee)
Okada, T., Fujieda, S., Seino, S., Nakagawa, T.: Evaluation of Magnetic Flux Density Change for Vibration Energy Harvesting: Comparison Between Direct and Indirect Measurements. 2023 IEEE International Magnetic Conference
Subudhi, P., Sagar, V., Kumar, S., Punetha, D.: Simulation and optimization of substrate layer material for PVDF cantilever based vibration energy harvesting system. IEEE Sens. J. 23(23) (2023)
Abouzarkhanifard, A., Chimeh, H.E., Nabavi, S., Al Janaideh, M., Zhang, L.: Zero-power MEMS resonant mass sensor inspired by piezoelectric vibration energy harvesting. 2023 IEEE Sensors Applications Symposium (SAS)
Bybi, A., Benhiba, A., Lahlouh, I., Ammar, A., Et-Tahir, A., Drissi, H.: Investigation of Vibrations Energy Harvesting from Vehicle Suspension System and Modeling Using Electrical Equivalent Circuits. 2023 3rd International Conference on Electrical, Computer, Communications and Mechatronics Engineering (ICECCME)
Feng, Z., Peng, H., Kang, Y.: Complex impedance matching for electromagnetic vibration energy harvesting: key parameters and low power consumption implementation. IEEE Transact. Power Electron. 38(12) (2023)
Sun, G., Sheng, L., Luo, L., Yu, H.: Game theoretic approach for multipriority data transmission in 5G vehicular networks. IEEE Trans. Intell. Transp. Syst. 23(12), 24672–24685 (2022). https://doi.org/10.1109/TITS.2022.3198046
Li, Y., Luo, Y., Wu, X., Shi, Z., Ma, S., Yang, G.: Variational bayesian learning based localization and channel reconstruction in RIS-aided systems. IEEE Transact. Wireless Commun. (2024). https://doi.org/10.1109/TWC.2024.3380903
Wang, Y., Yu, A., Cheng, Y., Qi, J.: Matrix diffractive deep neural networks merging polarization into meta-devices. Laser Photon. Rev. 18(2), 2300903 (2024). https://doi.org/10.1002/lpor.202300903
Yang, Y., Zhang, Z., Zhou, Y., Wang, C., Zhu, H.: Design of a simultaneous information and power transfer system based on a modulating feature of magnetron. IEEE Trans. Microw. Theory Tech. 71(2), 907–915 (2023). https://doi.org/10.1109/TMTT.2022.3205612
Zha, S., Qu, Z., Zhang, J., Zheng, D., Liu, P.: A gain reconfigurable reflector antenna with surface mounted field-induced artificial magnetic conductor for adaptive HIRF prevention. IEEE Trans. Antennas Propag. (2024). https://doi.org/10.1109/TAP.2024.3434371
Ma, Y., Li, T., Zhou, Y., Yu, L., Jin, D.: Mitigating energy consumption in heterogeneous mobile networks through data-driven optimization. IEEE Trans. Netw. Serv. Manage. 21(4), 4369–4382 (2024). https://doi.org/10.1109/TNSM.2024.3416947
Proakis, J.G.: Digital Communications, 4th edn. Mac Graw Hill
Xi, Y., Burr, A., Wei, J.B., Grace, D.: A general upper bound to evaluate packet error rate over quasi-static fading channels. IEEE Trans. Wireless Commun. 10(5), 1373–1377 (2011)
Mathai, A.M., Saxena, R.K., Haubold, H.J.: The H-function: Theory and applications. Springer science (2010)
Acknowledgements
This Research is funded by Researchers Supporting Project No. (RSPD2024R553), King Saud University, Riyadh, Saudi Arabia.
Funding
A fund from KSU has been received.
Author information
Authors and Affiliations
Contributions
This is the contribution of Prof. Hatem Boujemaa, Prof. Musaed Alhussein and Prof. Ghaya Rekaya.
Corresponding author
Ethics declarations
Conflict of interest
No Conflict of interest for this article.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix A
Appendix A
The variable \(\mathcal {Y}=\alpha \times \mathcal {F}\) where \(\mathcal {F}\) is the frequency of mechanical vibrations has a Gaussian distribution written as
The Mellin Tranform (MT) of \(\mathcal {Y}\) is computed as
We deduce
Let \(y=\frac{x^2}{2\alpha ^2\sigma _{\mathcal {F}}^2}\), we deduce
where \(\varGamma (.)\) is the Gamma function.
The variable \(\mathcal {X}=\mathcal {D}^2\) where \(\mathcal {D}\) is the mechanical deformation has a non-central zeta-square distribution with one degree of freedom and PDF given by
where \(I_m(x)\) is the modified Bessel function of the first kind and k-th order.
The Mellin transform of PDF of \(\mathcal {X}\) is equal to
We have
We deduce
The transmitted energy per symbol \(E_s=\mathcal {X}\mathcal {Y}\). As \(\mathcal {X}\) and \(\mathcal {Y}\) are independent, we have
The PDF of \(E_s\) is computed using the inverse MT
Therefore, we have
We deduce the expression of the PDF of \(E_s\)
where \(H_{m,n}^{p,q}()\) is the Fox H function [29].
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Boujemaa, H., Alhussein, M. & Rekaya, G. Simultaneously transmitting and reflecting reconfigurable intelligent surfaces with energy harvesting from vibrations. SIViP 19, 84 (2025). https://doi.org/10.1007/s11760-024-03643-x
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s11760-024-03643-x