Abstract
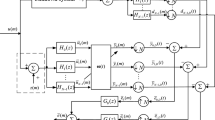
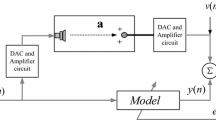
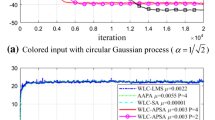
The performance of the affine projection algorithm (APA) is negatively affected when confronted with non-Gaussian noises and impulsive background noises. In order to mitigate this problem, this paper introduces the Affine Projection Exponential Hyperbolic Sine Algorithm (APEHSA), which employs a cost function that is derived from the exponential hyperbolic sine-based error function. The proposed algorithm is effectively adopted in adaptive filtering due to its ability to handle non-Gaussian and impulsive background noises. To enhance the rate of convergence and address the issue of steady-state misalignment in the APEHSA, the incorporation of the variable scaling parameter method has been introduced. Hence, the Variable Scaling Parameter APEHSA (VSP-APEHSA) is proposed. Furthermore, the mean square stability and the steady-state performance of the proposed algorithm are analyzed. In order to assess the effectiveness of the APEHSA, a series of simulation studies were conducted in the context of system identification scenarios and acoustic echo cancellation (AEC) system. The results of these studies demonstrate that the APEHSA algorithm exhibits superior steady state performance and enhanced convergence capabilities compared to other established algorithms, including APA, Exponential Hyperbolic Sine Adaptive Filter (EHSAF), affine projection tanh algorithm (APTA), and Affine Projection Sign Algorithm (APSA), particularly in impulsive noise environments.










Similar content being viewed by others
Data availability
No datasets were generated or analysed during the current study.
References
Bajić, I.V., Mrak, M., Dufaux, F., Magli, E., Chen, T.: Multimedia signal processing: a history of the multimedia signal processing technical committee. IEEE Signal Process. Mag. 40(4), 72–79 (2023)
Elbir, A.M., Mishra, K.V., Vorobyov, S.A., Heath, R.W.: Twenty-five years of advances in beamforming: From convex and nonconvex optimization to learning techniques. IEEE Signal Process. Mag. 40(4), 118–131 (2023)
Zavala-Mondragón, L.A., With, P.H.N., Sommen, F.: A signal processing interpretation of noise-reduction convolutional neural networks: exploring the mathematical formulation of encoding-decoding cnns. IEEE Signal Process. Mag. 40(7), 38–63 (2023)
Engelberg, S.: Implementing moving average filters using recursion. IEEE Signal Process. Mag. 40(7), 78–80 (2023)
Engelberg, S.: Periodograms and the method of averaged periodograms [lecture notes]. IEEE Signal Process. Mag. 40(6), 83–91 (2023)
Leus, G., Marques, A.G., Moura, J.M.F., Ortega, A., Shuman, D.I.: Graph signal processing: history, development, impact, and outlook. IEEE Signal Process. Mag. 40(4), 49–60 (2023)
Yan, Y., Kuruoglu, E.E., Altinkaya, M.A.: Adaptive sign algorithm for graph signal processing. Signal Process. 200, 108662 (2022)
Zheng, Z., Zhao, H.: Affine projection m-estimate subband adaptive filters for robust adaptive filtering in impulsive noise. Signal Process. 120, 64–70 (2016)
Wang, W., Doğançay, K.: Widely linear adaptive filtering based on clifford geometric algebra: a unified framework [hypercomplex signal and image processing]. IEEE Signal Process. Mag. 41(2), 86–101 (2024). https://doi.org/10.1109/MSP.2024.3379732
Kwong, R.H., Johnston, E.W.: A variable step size lms algorithm. IEEE Trans. Signal Process. 40(7), 1633–1642 (1992)
Benesty, J., Rey, H., Vega, L.R., Tressens, S.: A nonparametric vss nlms algorithm. IEEE Signal Process. Lett. 13(10), 581–584 (2006)
Bhattacharjee, S.S., Kumar, K., George, N.V.: Nearest kronecker product decomposition based generalized maximum correntropy and generalized hyperbolic secant robust adaptive filters. IEEE Signal Process. Lett. 27, 1525–1529 (2020)
Kumar, K., Pandey, R., Bhattacharjee, S.S., George, N.V.: Exponential hyperbolic cosine robust adaptive filters for audio signal processing. IEEE Signal Process. Lett. 28, 1410–1414 (2021)
Radhika, S., Albu, F., Chandrasekar, A.: Robust exponential hyperbolic sine adaptive filter for impulsive noise environments. IEEE Trans. Circuits Syst. II Expr. Br. 69(12), 5149–5153 (2022)
Ozeki, K., Umeda, T.: An adaptive filtering algorithm using an orthogonal projection to an affine subspace and its properties. Electron. Commun. Jpn (Part I: Communications) 67(5), 19–27 (1984)
Kim, S.-E., Kong, S.-J., Song, W.-J.: An affine projection algorithm with evolving order. IEEE Signal Process. Lett. 16(11), 937–940 (2009)
Rusu, A.-G., Dogariu, L.-M., Costea, R.-L., Paleologu, C., Benesty, J., Ciochină, S.: A variable step-size affine projection algorithm based on data reuse. In: 2022 45th International Conference on Telecommunications and Signal Processing (TSP), pp. 399–402 (2022). IEEE
Hur, J., Lee, M., Kim, D., Park, P.: A variable step-size robust saturation algorithm against impulsive noises. IEEE Trans. Circuits Syst. II Expr.Br. 67(10), 2279–2283 (2019)
Shao, T., Zheng, Y.R., Benesty, J.: An affine projection sign algorithm robust against impulsive interferences. IEEE Signal Process. Lett. 17(4), 327–330 (2010)
Zhang, Q., Wang, S., Lin, D., Chen, S.: Robust affine projection tanh algorithm and its performance analysis. Signal Process. 202, 108749 (2023)
Huang, F., Zhang, J., Zhang, S.: Affine projection versoria algorithm for robust adaptive echo cancellation in hands-free voice communications. IEEE Trans. Veh. Technol. 67(12), 11924–11935 (2018)
Song, P., Zhao, H.: Affine-projection-like m-estimate adaptive filter for robust filtering in impulse noise. IEEE Trans. Circuits Syst. II Expr. Br. 66(12), 2087–2091 (2019)
Wang, X., Han, J.: Affine projection algorithm based on least mean fourth algorithm for system identification. IEEE Access 8, 11930–11938 (2020)
Karal, O.: Maximum likelihood optimal and robust support vector regression with lncosh loss function. Neural Netw. 94, 1–12 (2017)
Kuruoglu, E.E., Rayner, P.J., Fitzgerald, W.J.: Least l/sub p/-norm estimation of autoregressive model coefficients of symmetric/spl alpha/-stable processes. IEEE Signal Process. Lett. 4(7), 201–203 (1997)
Ni, J., Chen, X., Yang, J.: Two variants of the sign subband adaptive filter with improved convergence rate. Signal Process. 96, 325–331 (2014)
Kuruoǧlu, E.E.: Nonlinear least lp-norm filters for nonlinear autoregressive \(\alpha \)-stable processes. Digit. Signal Process. 12(1), 119–142 (2002)
Aydin, G., Arikan, O., Cetin, A.E.: Robust adaptive filtering algorithms for/spl alpha/-stable random processes. IEEE Trans. Circuits Syst. II Analog Digit. Signal Process. 46(2), 198–202 (1999)
Radhika, S., Albu, F., Chandrasekar, A.: Steady state mean square analysis of standard maximum versoria criterion based adaptive algorithm. IEEE Trans. Circuits Syst. II Expr. Br. 68(4), 1547–1551 (2020)
Acknowledgements
This work was partially supported by National Natural Science Foundation of China (grant: 62101215), the Natural Science Foundation of Jiangsu Province (grant: BK20210450), the Fundamental Research Funds for the Central Universities (grant: JUSRP121021) and the National Key R&D Program of China (2022YFD2100401).
Author information
Authors and Affiliations
Contributions
FS was involved in the formal analysis, methodology, investigation, Writing, original draft preparation,review and editing. WXY and WYW contributed to review, editing and Supervision. All authors participated in the analysis and interpretation of the findings, and made substantial contributions to the completion of the final manuscript.
Corresponding authors
Ethics declarations
Conflict of interest
The authors declare no Conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Shen, F., Yan, W. & Wang, W. Affine projection exponential hyperbolic sine algorithm designed for impulsive noise environments. SIViP 19, 104 (2025). https://doi.org/10.1007/s11760-024-03702-3
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s11760-024-03702-3