Abstract
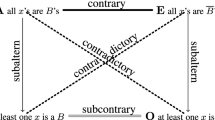
The hexagon of opposition is an improvement of the square of opposition due to Robert Blanché. After a short presentation of the square and its various interpretations, we discuss two important problems related with the square: the problem of the I-corner and the problem of the O-corner. The meaning of the notion described by the I-corner does not correspond to the name used for it. In the case of the O-corner, the problem is not a wrong-name problem but a no-name problem and it is not clear what is the intuitive notion corresponding to it. We explain then that the triangle of contrariety proposed by different people such as Vasiliev and Jespersen solves these problems, but that we don’t need to reject the square. It can be reconstructed from this triangle of contrariety, by considering a dual triangle of subcontrariety. This is the main idea of Blanché’s hexagon. We then give different examples of hexagons to show how this framework can be useful to conceptual analysis in many different fields such as economy, music, semiotics, identity theory, philosophy, metalogic and the metatheory of the hexagon itself. We finish by discussing the abstract structure of the hexagon and by showing how we can swing from sense to non-sense thinking with the hexagon.
Similar content being viewed by others
References
Badir, S.: How the semiotic square came. In [9], pp. 427–442 (2012)
Beziau J.-Y.: New light on the square of oppositions and its nameless corner. Log. Investig. 10, 218–232 (2003)
Beziau J.-Y.: The new rising of the square. In: Beziau, J.-Y., Jacquette, D. (eds.) Around and Beyond the Square of Opposition., Birkhäuser, Basel (2012)
Beziau J.-Y.: History of the concept of truth-value. In: Gabbay, D.M., Woods, J. (eds.) Handbook of the History of Logic, vol. 11, pp. 233–305. Elsevier, Amsterdam (2012)
Beziau J.-Y. et al.: Let be antilogic: anticlassical logic as a logic. In: Moktefi, A. (eds.) Soyons Logique, College Publication, London (2012)
Beziau J.-Y., (ed.): La Pointure du Symbole. Editions Pétra, Paris (2012)
Beziau, J.-Y., Jacquette, D. (eds.): Around and Beyond the Square of Opposition. Birkhäuser, Basel (2012)
Beziau, J.-Y., Payette, G. (eds.): Special issue on the square of opposition. Logica Universalis 2(1) (2008)
Beziau, J.-Y., Payette, G. (eds.): The Square of Opposition—A General Framework for Cognition. Peter Lang, Bern (2012)
Blanché R.: Quantity, modality, and other kindred systems of categories. Mind 61, 369–375 (1952)
Blanché R.: Sur l’opposition des concepts. Theoria 19, 89–130 (1953)
Blanché R.: Opposition et négation. Revue Philosophique 167, 187–216 (1957)
Blanché R.: Sur la structuration du tableau des connectifs interpropositionnels binaires. J. Symb. Log. 22, 17–18 (1957)
Blanché R.: Structures intellectuelles. Vrin, Paris (1966)
Blanché R.: Sur le système des connecteurs interpropositionnels. Cahiers pour l’Analyse 10, 131–149 (1969)
Boethius, Institutio Musica. ca 505. English translation: C.M. Bower, Fundamentals of Music. Yale University Press, New Haven (1989)
Bréal M.: Essai de sémantique: science des significations. Hachette, Paris (1897)
Cartier, P.: How to take advantage of the blur between the finite and the infinite. Logica Universalis 6 (2012). doi:10.1007/s11787-012-0043-z
Dubois, D., Prade, H.: From Blanché’s hexagonal organization of concepts to formal concept analysis and possibility theory. Logica Universalis 6 (2012). doi:10.1007/s11787-011-0039-0
Dufatanye, A.-A.: From the logical square to Blanché’s hexagon: formalization, applicability and the idea of the normative structure of thought. Logica Universalis 6 (2012). doi:10.1007/s11787-012-0040-2
Fellbaum C.: Wordnet, an Electronic Lexical Database for English. MIT Press, Cambridge (1998)
Granger G.G.: Pensée formelle et sciences de l’homme. Aubier, Paris (1960)
Grattan-Guinness I.: Omnipresence, multipresence and ubiquity: kinds of generality in and around mathematics and logics. Logica Universalis 5, 21–73 (2011)
Grigg R.: Lacan and Badiou: logic of the “pas-tout”. Filozofski vestnik 26, 53–65 (2005)
Grize J.-B.: Des carrés qui ne tournent pas rond et de quelques autres. Travaux du centre de recherches sémiologiques 56, 139–152 (1988)
Guitart, R.: A hexagonal framework of the field F4 and the associated Borromean Logic. Logica Universalis 6 (2012). doi:10.1007/s11787-011-0033-6
van Heijenoort J.: Review of [13]. J. Symb. Log. 24, 228 (1959)
Hoeksema, J.: Blocking Effects and Polarity Sensitivity. In: Essays dedicated to Johan van Benthem on the Occasion of his 50th Birthday. Amsterdam University Press, Amsterdam (1999)
Horn L.R.: A Natural History of Negation. University Chicago Press, Chicago (1989)
Jaspers, D.: Logic and colour. Logica Universalis 6 (2012). doi:10.1007/s11787-012-0044-y
Jespersen O.: Negation in English and Other Languages. A.F. Host and Son, Copenhagen (1917)
Joerden, J.C.: Deontological square, hexagon, and decagon: a deontic framework for supererogation. Logica Universalis 6 (2012). doi:10.1007/s11787-012-0041-1
Kant, I.: Logik (Jäsche), 1800. English translation in Lectures on Logic, translated and edited by J. M. Young, Cambridge University Press, Cambridge (1992)
Lacan, J.: Le séminaire XX—Encore, Seuil, Paris, 1972–73. English translation: Jacques-Alain Miller (ed.) The Seminar XX, Encore: On Feminine Sexuality, the Limits of Love and Knowledge; transl. by Bruce Fink. W.W. Norton and Co., New York (1998)
Lacan J.: L’Étourdit. Scilicet Paris 6, 5–52 (1973)
Lévi-Strauss, C.: Les structures élémentaires de la parenté. PUF, Paris (1949)
Łukasiewicz J.: Logice trójwartościowej. Ruch Filozoficny 5, 170–171 (1920)
Łukasiewicz J.: Aristotle’s Syllogistic from the Standpoint of Modern Logic. Clarendon, Oxford (1951)
Łukasiewicz J.: A system of modal logic. J. Comput. Syst. 1, 111–149 (1953)
Luzeaux D., Sallantin J., Dartnell C.: Logical extensions of Aristotle’s square. Logica Universalis 2, 167–187 (2008)
Moretti, A.: Geometry of modalities? Yes: through n-opposition theory. In: Beziau, J.-Y., Costa Leite, A., Facchini, A. (eds.) Aspects of Universal Logic, Travaux de logique, vol. 17, pp. 102–145, Neuchâtel (2004)
Moretti, A.: The geometry of logical opposition. PhD thesis, University of Neuchâtel (2009)
Moretti, A.: Why the logical hexagon? Logica Universalis 6 (2012). doi:10.1007/s11787-012-0045-x
Parsons, T.: The traditional square of opposition. Stanford Encyclopedia of Philosophy (2006, online)
Parsons T.: Things that are right with the traditional square of opposition. Logica Universalis 2, 3–11 (2008)
Pellissier R.: “Setting” n-opposition. Logica Universalis 2, 235–263 (2008)
Sesmat A.: Logique II. Les raisonnements, la logistique. Hermann, Paris (1951)
Seuren P.M.: The Logic of Language—Language from within Volume II. Oxford University Press, Oxford (2010)
Sigman M., Cecchi G.A.: Global organization of the Wordnet lexicon. Proc. Natl. Acad. Sci. 99, 1742–1747 (2002)
Simons, P.: Approaching the alethic modal hexagon of opposition. Logica Universalis 6 (2012). doi:10.1007/s11787-012-0042-0
Smessaert, H.: The classical Aristotelian hexagon versus the modern duality hexagon. Logica Universalis 6 (2012). doi:10.1007/s11787-011-0031-8
Smith N.B.: The idea of the French hexagon. French Hist. Stud. 6, 139–155 (1969)
Sullivan M.W.: Apuleian Logic. The Nature, Sources, and Influence of Apuleius’s Peri Hermeneias. North-Holland, Amsterdam (1967)
Tarski A.: Drei Briefe an Otto Neurath. 1936 published in Grazer Philosophische Studien 43, 1–32 (1992)
Tiles M., Jinmei Y.: Could the Aristotelian square of opposition be translated into Chinese?. Dao J. Comp. Philos. 4, 137–149 (2004)
Vasiliev, N.: On partial judgements, the triangle of opposites and the law of excluded fourth. Scientific Papers of Kazan University (1910) (in Russia)
Wajsberg M.: Ein erweiterter Klassenkalkül. Monatshefte fur Mathematik und Physik 4, 113–126 (1933)
Weil, A.: Sur l’étude algébrique de certains types de lois du mariage. Appendix in [36], pp. 257–272 (1949)
Weil, A.: Souvenirs d’apprentissage. Birkhäuser, Basel (1991); English translation: The Apprenticeship of a Mathematician. Birkhäuser, Basel (1992)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Béziau, JY. The Power of the Hexagon. Log. Univers. 6, 1–43 (2012). https://doi.org/10.1007/s11787-012-0046-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11787-012-0046-9