Equality of average and steady-state levels in some nonlinear models of biological oscillations

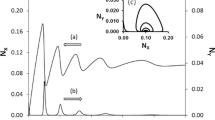
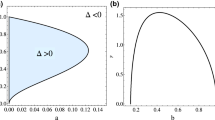
Abstract

Nonlinear oscillatory systems, playing a major role in biology, do not exhibit harmonic oscillations. Therefore, one might assume that the average value of any of their oscillating variables is unequal to the steady-state value. For a number of mathematical models of calcium oscillations (e.g. the Somogyi–Stucki model and several models developed by Goldbeter and co-workers), the average value of the cytosolic calcium concentration (not, however, of the concentration in the intracellular store) does equal its value at the corresponding unstable steady state at the same parameter values. The average value for parameter values in the unstable region is even equal to the level at the stable steady state for other parameter values, which allow stability. This holds for all parameters except those involved in the net flux across the cell membrane. We compare these properties with a similar property of the Higgins–Selkov model of glycolytic oscillations and two-dimensional Lotka–Volterra equations. Here, we show that this equality property is critically dependent on the following conditions: There must exist a net flux across the model boundaries that is linearly dependent on the concentration variable for which the equality property holds plus an additive constant, while being independent of all others. A number of models satisfy these conditions or can be transformed such that they do so. We discuss our results in view of the question which advantages oscillations may have in biology. For example, the implications of the findings for the decoding of calcium oscillations are outlined. Moreover, we elucidate interrelations with metabolic control analysis.