Culture–area relation in Axelrod’s model for culture dissemination

Abstract

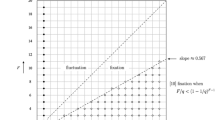
Axelrod’s model for culture dissemination offers a nontrivial answer to the question of why there is cultural diversity given that people’s beliefs have a tendency to become more similar to each other’s as they interact repeatedly. The answer depends on the two control parameters of the model, namely, the number F of cultural features that characterize each agent, and the number q of traits that each feature can take on, as well as on the size A of the territory or, equivalently, on the number of interacting agents. Here, we investigate the dependence of the number C of distinct coexisting cultures on the area A in Axelrod’s model, the culture–area relationship, through extensive Monte Carlo simulations. We find a non-monotonous culture–area relation, for which the number of cultures decreases when the area grows beyond a certain size, provided that q is smaller than a threshold value q _c = q _c (F) and F ≥ 3. In the limit of infinite area, this threshold value signals the onset of a discontinuous transition between a globalized regime marked by a uniform culture (C = 1), and a completely polarized regime where all C = q ^F possible cultures coexist. Otherwise, the culture–area relation exhibits the typical behavior of the species–area relation, i.e., a monotonically increasing curve the slope of which is steep at first and steadily levels off at some maximum diversity value.