Abstract
It has often been asked which physiological advantages calcium (Ca2+) oscillations in non-excitable cells may have as compared to an adjustable stationary Ca2+ signal. One of the proposed answers is that an oscillatory regime allows a lowering of the average Ca2+ concentration, which is likely to be advantageous because Ca2+ is harmful to the cell in high concentrations. To check this hypothesis, we apply Jensen’s inequality to study the relation between the average Ca2+ concentration during oscillations and the Ca2+ concentration at the (unstable) steady state. Jensen’s inequality states that for a (strictly) convex function, the function value of the average of a set of argument values is lower than the average of the function values of the arguments from that set. We show that the kinetics of the Ca2+ efflux out of the cell is crucial in this context. By analytical calculations we derive that, if the Ca2+ efflux is a convex function of the cytosolic Ca2+ concentration, then oscillations lower the average Ca2+ concentration in comparison to the unstable steady state. If it is a concave function, the average Ca2+ concentration is increased, while it remains the same if that function is linear. We also analyse the case where the efflux obeys a Hill kinetics, which involves both a convex and a concave part. The results are illustrated by numerical simulations and simple example models. The theoretical predictions are tested with three experimental data sets from the literature. In two of them, the average appears to be higher than the steady-state value, while the third points to approximate equality. Thus oscillations may be used in real cells to tune the average Ca2+ concentration in both directions.







Similar content being viewed by others
Abbreviations
- K :
-
Dissociation constant of CICR
- k 2 :
-
Rate constant of pumping Ca2+ from the cytosol into the intracellular stores
- k 3 :
-
Rate constant of CICR
- k f :
-
Rate constant of the leak efflux
- K S :
-
Half-saturation constant
- n :
-
Hill coefficient
- t :
-
Time
- f(Z):
-
Vout efflux function out of the cell
- V in :
-
Influx function into the cell
- V pump :
-
ATPase pumping Ca2+ from the cytosol into the intracellular stores
- V CICR :
-
Ca2+ release out of the ER following the CICR
- V leak :
-
Leak flux out of the intracellular stores
- Y :
-
Overall concentration of Ca2+ in the intracellular stores
- Y i :
-
Concentration of Ca2+ in one of the intracellular stores
- Z :
-
Concentration of Ca2+ in the cytosol
- Z ss :
-
Steady-state concentration of Ca2+ in the cytosol
- \( {\left\langle Z \right\rangle } \) :
-
Average concentration of Ca2+ in the cytosol
- CaM:
-
Calmodulin
- CICR:
-
Ca2+-induced Ca2+ release mechanism
- ER:
-
Endoplasmic reticulum
- IP3 :
-
Inositol-1,4,5-trisphosphate
- PMCA:
-
Plasma membrane Ca2+ ATPase
- SOCs:
-
Store-operated Ca2+ channels
- m:
-
Mitochondria
- ER:
-
Endoplasmic reticulum
References
Albrecht MA, Colegrove SL, Friel DD (2002) Differential regulation of ER Ca2+ uptake and release rates accounts for multiple modes of Ca2+-induced Ca2+ release. J Gen Physiol 119:211–233
Atri A, Amundson J, Clapham D, Sneyd J (1993) A single-pool model for intracellular calcium oscillations and waves in the Xenopus laevis oocyte. Biophys J 65:1727–1739
Berridge MJ (1989) Cell signalling through cytoplasmic calcium oscillations. In: Goldbeter A (ed) Cell to cell signalling: from experiment to theoretical models. Academic Press, London, pp 449–459
Berridge MJ (1997) Elementary and global aspects of calcium signalling. J Exp Biol 200(Pt2):315–319
Berridge MJ, Bootman MD, Lipp P (1998) Calcium—a life and death signal. Nature 395(6703):645–648
Berridge MJ, Bootman MD, Roderick HL (2003) Calcium signalling: dynamics, homeostasis and remodelling. Nat Rev Mol Cell Biol 4(7):517–529
Birch-Machin MA, Dawson AP (1988) Ca2+ transport by rat liver plasma membranes: the transporter and the previously reported Ca2+-ATPase are different enzymes. Biochim Biophys Acta 944(2):308–314
Borghans JM, Dupont G, Goldbeter A (1997) Complex intracellular Ca2+ oscillations: a theoretical exploration of possible mechanisms. Biophys Chem 66(1):25–41
Brewster JF, Graham MR, Mutch WA (2005) Convexity, Jensen’s inequality and benefits of noisy mechanical ventilation. J R Soc Interface 2:393–396
Bruce JI, Straub SV, Yule DI (2003) Crosstalk between cAMP and Ca2+ signaling in non-excitable cells. Cell Calcium 34:431–444
Camello P, Gardner J, Petersen OH, Tepikin AV (1996) Calcium dependence of calcium extrusion and calcium uptake in mouse pancreatic acinar cells. J Physiol 490:585–593
Carafoli E (1991a) Calcium pump of the plasma membrane. Physiol Rev 71:129–153
Carafoli E (1991b) The calcium pumping ATPase of the plasma membrane. Annu Rev Physiol 53:531–547
Carafoli E, Guerini D (1993) Molecular and cellular biology of plasma membrane calcium ATPase. Trends Cardiovasc Med 3:177–184
Delgado-Coello B, Trejo R, Mas-Oliva J (2006) Is there a specific role for the plasma membrane Ca2+-ATPase in the hepatocyte? Mol Cell Biochem 285(1–2):1–15
Dupont G, Goldbeter A (1993) One-pool model for Ca2+ oscillations involving Ca2+ and inositol 1,4,5-triphosphate as co-agonists for Ca2+ release. Cell Calcium 14:311–322
Dupont G, Goldbeter A (1998) CaM kinase II as frequency decoder of Ca2+ oscillations. Bioessays 20:607–610
Dupont G, Swillens S, Clair C, Tordjmann T, Combettes L (2000) Hierarchical organization of calcium signals in hepatocytes: from experiments to models. Biochim Biophys Acta 1498:134–152
Dupont G, Houart G, De Koninck P (2003) Sensitivity of CaM kinase II to the frequency of Ca2+ oscillations: a simple model. Cell Calcium 34:485–497
Dupont G, Combettes L, Leybaert L (2007) Calcium dynamics: spatio-temporal organization from the subcellular to the organ level. Int Rev Cytol 261:193–245
Evers C, Hugentobler G, Lester R, Gmaj P, Meier P, Murer H (1988) ATP-dependent Ca2+ uptake and Ca2+-dependent protein phosphorylation in basolateral liver plasma membranes. Biochim Biophys Acta 939(3):542–550
Falcke M (2004) Reading the patterns in living cells—the physics of Ca2+ signalling. Adv Phys 53:255–440
Fraleigh JB (1994) A first course in abstract algebra. Addison Wesley Publishing Company, Reading, MA
Gall D, Baus E, Dupont G (2000) Activation of the liver glycogen phosphorylase by Ca2+ oscillations: a theoretical study. J Theor Biol 207:445–454
Gaspers LD, Thomas AP (2005) Calcium signaling in liver. Cell Calcium 38(3–4):329–342
Goldbeter A (1996) Biochemical oscillations and cellular rhythms. Cambridge University Press, Cambridge
Goldbeter A, Dupont G, Berridge MJ (1990) Minimal model for signal-induced Ca2+ oscillations and for their frequency encoding through protein phosphorylation. Proc Natl Acad Sci USA 87(4):1461–1465
Grubelnik V, Larsen AZ, Kummer U, Olsen LF, Marhl M (2001) Mitochondria regulate the amplitude of simple and complex calcium oscillations. Biophys Chem 94:59–74
Hardy GH, Littlewood JE, Pólya G (1988) Inequalities, 2nd edn. Cambridge University Press, Cambridge
Hauser MJB, Kummer U, Larsen AZ, Olsen LF (2001) Oscillatory dynamics protect enzymes and possibly cells against toxic substances. Faraday Discuss 120:215–227
Heinrich R, Schuster S (1996) The regulation of cellular systems. Chapman and Hall, New York
Höfer T (1999) Model of intercellular calcium oscillations in epatocytes: synchronization of heterogeneous cells. Biophys J 77:1244–1256
Houart G, Dupont G, Goldbeter A (1999) Bursting, chaos and birhythmicity originating from self-modulation of the inositol 1,4,5-trisphosphate signal in a model for intracellular Ca2+ oscillations. Bull Math Biol 61:507–530
Jacob R (1990) Calcium oscillations in electrically non-excitable cells. Biochim Biophys Acta 1052:427–438
Jensen JLWV (1906) Sur les fonctions convexes et les inégalités entre les valeurs moyennes. Acta Math 30:175–193
Keizer J, De Young G (1994) Simplification of a realistic model of IP3-induced Ca2+ oscillations. J Theor Biol 166:431–442
Kessler F, Bennardini F, Bachs O, Serratosa J, James P, Caride AJ, Gazzotti P, Penniston JT, Carafoli E (1990) Partial purification and characterization of the Ca2(+)-pumping ATPase of the liver plasma membrane. J Biol Chem 265(26):16012–16019
Knoke B, Marhl M, Perc M, Schuster S (2008) Equality of average and steady-state levels in some nonlinear models of biological oscillations. Theory Biosci 127:1–14
Kowalewski JM, Uhlen P, Kitano H, Brismar H (2006) Modeling the impact of store-operated Ca2+ entry on intracellular Ca2+ oscillations. Math Biosci 204:232–249
Krantz SG (1999) Jensen’s Inequality. §9.1.3 in Handbook of complex variables. Boston MA, Birkhäuser, p 118
Kummer U, Olsen LF, Dixon CJ, Green AK, Bornberg-Bauer E, Baier G (2000) Switching from simple to complex oscillations in calcium signaling. Biophys J 79:1188–1195
Li YX, Goldbeter A (1992) Pulsatile signaling in intercellular communication. Biophys J 61:161–171
Li YX, Rinzel J (1994) Equations for InsP3 receptor-mediated [Ca2+]i oscillations derived from a detailed kinetic model: a Hodgkin-Huxley like formalism. J Theor Biol 166(4):461–473
Li YX, Rinzel J, Keizer J, Stojilkovic SS (1994) Calcium oscillations in pituitary gonadotrophs: comparison of experiment and theory. Proc Natl Acad Sci USA 91:58–62
Li Y, Stojilkovic S, Keizer J, Rinzel J (1997) Sensing and refilling calcium stores in an excitable cell. Biophys J 72:1080–1091
Lin SH (1985) Novel ATP-dependent calcium transport component from rat liver plasma membranes. The transporter and the previously reported (Ca2+-Mg2+)-ATPase are different proteins. J Biol Chem 260(13):7850–7856
Marhl M, Schuster S, Brumen M, Heinrich R (1997) Modelling the interrelations between calcium oscillations and ER membrane potential oscillations. Biophys Chem 63:221–239
Marhl M, Haberichter T, Brumen M, Heinrich R (2000) Complex calcium oscillations and the role of mitochondria and cytosolic proteins. Biosystems 57:75–86
Marhl M, Perc M, Schuster S (2006) A minimal model for decoding of time-limited Ca2+ oscillations. Biophys Chem 120:161–167
Marrero I, Green AK, Cobbold PH, Dixon CJ (1996) Bovine growth hormone induces oscillations in cytosolic free Ca2+ in single rat hepatocytes. Biochem J 313(Pt 2):525–528
Martin TL, Huey RB (2008) Why “suboptimal” is optimal: Jensen’s inequality and ectotherm thermal preferences. Am Nat 171:E102–E118
Mauger JP, Poggioli J, Guesdon F, Claret M (1984) Noradrenaline, vasopressin and angiotensin increase Ca2+ influx by opening a common pool of Ca2+ channels in isolated rat liver cells. Biochem J 221(1):121–127
Olsen LF, Hauser MJB, Kummer U (2003) Mechanism of protection of peroxidase activity by oscillatory dynamics. Eur J Biochem (FEBS) 270:2796–2804
Prpić V, Green KC, Blackmore PF, Exton JH (1984) Vasopressin-, angiotensin II-, and alpha 1-adrenergic-induced inhibition of Ca2+ transport by rat liver plasma membrane vesicles. J Biol Chem 259(3):1382–1385
Putney JW Jr (1998) Calcium signalling: up, down, up, down. What’s the point? Science 279:191–192
Rapp PE, Mees AI, Sparrow CT (1981) Frequency encoded biochemical regulation is more accurate than amplitude dependent control. J Theor Biol 90(4):531–544
Rooney TA, Sass EJ, Thomas AP (1989) Characterization of cytosolic calcium oscillations induced by phenylephrine and vasopressin in single fura-2-loaded hepatocytes. J Biol Chem 264:17131–17141
Rychkov GY, Litjens T, Roberts ML, Barritt GJ (2005) ATP and vasopressin activate a single type of store-operated Ca2+ channel, identified by patch-clamp recording, in rat hepatocytes. Cell Calcium 37(2):183–191
Salazar C, Politi AZ, Höfer T (2008) Decoding of Ca2+ oscillations by phosphorylation cycles: analytic results. Biophys J 94(4):1203–1215
Schuster S, Marhl M, Höfer T (2002) Modelling of simple and complex calcium oscillations. From single-cell responses to intercellular signalling. Eur J Biochem 69:1333–1355
Skupin A, Kettenmann H, Winkler U, Wartenberg M, Sauer H, Tovey SC, Taylor CW, Falcke M (2008) How does intracellular Ca2+ oscillate: by chance or by the clock? Biophys J 94(6):2404–2411
Sneyd J, Tsaneva-Atanasova K, Yule DI, Thompson JL, Shuttleworth TJ (2004) Control of calcium oscillations by membrane fluxes. Proc Natl Acad Sci U S A 101(5):1392–1396
Somogyi R, Stucki JW (1991) Hormone-induced calcium oscillations in liver cells can be explained by a simple one pool model. J Biol Chem 266:11068–11077
Szekely D, Brennan SC, Mun H-C, Conigrave AD, Kuchel PW (2009) Effectors of the frequency of calcium oscillations in HEK-293 cells: wavelet analysis and a computer model. Eur Biophys J 39:149–165
Thul R, Bellamy TC, Roderick HL, Bootman MD, Coombes S (2008) Calcium oscillations. Adv Exp Med Biol 641:1–27
Valant PA, Adjei PN, Haynes DH (1992) Rapid Ca2+ extrusion via the Na+/Ca2+ exchanger of the human platelet. J Membr Biol 130(1):63–82
Woods NM, Cuthbertson KS, Cobbold PH (1986) Repetitive transient rises in cytoplasmic free calcium in hormone-stimulated hepatocytes. Nature 319(6054):600–602
Acknowledgements
We would like to thank E.G. Schukat-Talamazzini for support with the image analysis of time series and Ines Heiland for stimulating discussions. Financial support by the German Federal Ministry of Education and Research (BMBF) within the HepatoSys programme is gratefully acknowledged.
Author information
Authors and Affiliations
Corresponding author
Appendix A: Analysis of the square-shaped signal with arbitrary baseline
Appendix A: Analysis of the square-shaped signal with arbitrary baseline
The general square-shaped Ca2+ signal is given by:
with the baseline Z 1 < Z 2. We can compute the average of Z(t) over one period T as:
where we have introduced the relative baseline 0 ≤ α = Z 1/Z 2 < 1. Next we calculate the average of f(Z(t)) (f being the Hill kinetics from Eq. 21) over one period:
From relations 13, 34 and 35, it follows:
Factoring out Z 2 on both sides and introducing the relative saturation μ = Z 2/K S, we can write:
This can be solved for μ:
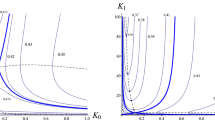
When plotting the allowed range of μ (the area below μcrit) over γ as in Fig. 4, we can see that it decreases with increasing α (see Fig. 7 with n = 2). This corresponds to increasing the baseline concentration of Ca2+.
Rights and permissions
About this article
Cite this article
Knoke, B., Bodenstein, C., Marhl, M. et al. Jensen’s inequality as a tool for explaining the effect of oscillations on the average cytosolic calcium concentration. Theory Biosci. 129, 25–38 (2010). https://doi.org/10.1007/s12064-010-0080-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12064-010-0080-1