Skip to main content

Advertisement

SpringerLink
Log in

On avian influenza epidemic models with time delay

  • Original Paper
  • Published:
Theory in Biosciences Aims and scope Submit manuscript

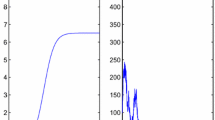
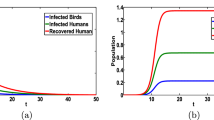
Abstract

After the outbreak of the first avian influenza A virus (H5N1) in Hong Kong in 1997, another avian influenza A virus (H7N9) crossed the species barrier in mainland China in 2013 and 2014 and caused more than 400 human cases with a death rate of nearly 40 %. In this paper, we take account of the incubation periods of avian influenza A virus and construct a bird-to-human transmission model with different time delays in the avian and human populations combining the survival probability of the infective avian and human populations at the latent time. By analyzing the dynamical behavior of the model, we obtain a threshold value for the prevalence of avian influenza and investigate local and global asymptotical stability of equilibria of the system.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4

Similar content being viewed by others

References

  • Agusto FB (2013) Optimal isolation control strategies and cost-effectiveness analysis of a two-strain avian influenza. BioSystems 113:155–164

    Article  CAS  PubMed  Google Scholar 

  • Alexander DJ (2007) An overview of the epidemiology of avian influenza. Vaccine 25:5637–5644

    Article  CAS  PubMed  Google Scholar 

  • Anderson RM, May RM (1991) Infectious diseases of humans: dynamics and control. Oxford University Press, Oxford

    Google Scholar 

  • Bao C, Cui L, Zhou M, Hong L, Wang H et al (2013) Live-animal markets and influenza A (H7N9) virus infection. N Engl J Med 368:2337–2339

    Article  CAS  PubMed  Google Scholar 

  • Beretta E, Takeuchi Y (1995) Global stability of an SIR model with time delays. J Math Biol 33:250–260

    Article  CAS  PubMed  Google Scholar 

  • Beretta E, Hara T, Ma W, Takeuchi Y (2001) Global asymptotical stability of an SIR epidemic model with distributed time delay. Nonlinear Anal 47:4107–4115

    Article  Google Scholar 

  • Bourouiba L, Gourley SA, Liu R, Wu J (2011) The interaction of migratory birds and domestic poultry and its role in sustaining avian influenza. SIAM J Appl Math 71:487–516

    Article  Google Scholar 

  • Centers for Disease Control and Prevention (CDC), Types of influenza virus. (August 3, 2011, Retrieved January 15, 2014). http://www.cdc.gov/flu/about/viruses/types.htm

  • Center for Infectious Disease Research and Policy (CIDRAP) (2013) China reports three H7N9 infections, two fatal. http://www.cidrap.umn.edu/news-perspective/2013/04/china-reports-three-h7n9-infections-two-fatal. Accessed 1 April 1 2013

  • Chong NS, Tchuenche JM, Smith RJ (2014) A mathematical model of avian influenza with half-saturated incidence. Theory Biosci 133:23–38

    Article  PubMed  Google Scholar 

  • Cooke KL, Grossman Z (1982) Discrete delay, distributed delay and stability switches. J Math Anal Appl 86:592–627

    Article  Google Scholar 

  • Cooke KL, Van Den Driessche P (1996) Analysis of an SEIRS epidemic model with two delays. J Math Biol 35:240–260

    Article  CAS  PubMed  Google Scholar 

  • Chen Y, Liang W, Yang S, Wu N, Gao H et al (2013) Human infections with the emerging avian influenza A H7N9 virus from wet market poultry: clinical analysis and characterisation of viral genome. Lancet 381:1916–1925

    Article  CAS  PubMed  Google Scholar 

  • Gao H et al (2013) Clinical findings in 111 cases of influenza A(H7N9) virus infection. N Engl J Med 368:2277–2285

    Article  CAS  PubMed  Google Scholar 

  • Gourley SA, Liu R (2010) Spatiotemporal distributions of migratory birds: patchy models with delay. SIAM J Appl Dyn Syst 9:589–610

    Article  Google Scholar 

  • Gumel AB (2009) Global dynamics of a two-strain avian influenza model. Int J Comput Math 86:85–108

    Article  Google Scholar 

  • Hale JK (1977) Theory of functional differential equations. Springer, Heidelberg

    Book  Google Scholar 

  • Huang G, Takeuchi Y, Ma W, Wei D (2010) Global stability for delay SIR and SEIR epidemic models with nonlinear incidence rate. Bull Math Biol 72:1192–1207

    Article  PubMed  Google Scholar 

  • Iwami S, Takeuchi Y, Liu X (2007) Avian-human influenza epidemic model. Math Biosci 207:1–25

    Article  PubMed  Google Scholar 

  • Iwami S, Takeuchi Y, Liu X (2009a) Avian flu pandemic: can we prevent it? J Theor Biol 257:181–190

  • Iwami S, Takeuchi Y, Liu X, Nakaoka S (2009b) A geographical spread of vaccine-resistance in avian influenza epidemics. J Theor Biol 259:219–228

  • Jung E, Iwami S, Takeuchi Y, Jo T-C (2009) Optimal control strategy for prevention of avian influenza pandemic. J Theor Biol 260:220–229

    Article  PubMed  Google Scholar 

  • Keeling MJ, Rohani P (2008) Modeling infectious diseases in humans and animals. Princeton University Press, Princeton

    Google Scholar 

  • Li Q, Zhou L, Zhou M, Chen Z, Li F, Wu H, Xiang N, Chen E et al (2014) Epidemiology of human infections with avian influenza A (H7N9) virus in China. N Engl J Med 370:520–532

    Article  CAS  PubMed  Google Scholar 

  • Liu S, Ruan S, Zhang X (2015) Nonlinear dynamics of avian influenza epidemic models. Math Biosci (submitted)

  • Lucchetti J, Roy M, Martcheva M (2009) An avian influenza model and its fit to human avian influenza cases. In: Tchuenche M, Mukandavire Z (eds) Advances in disease epidemiology. J. Nova Science Publishers, New York, pp 1–30

    Google Scholar 

  • Ma X, Wang W (2010) A discrete model of avian influenza with seasonal reproduction and transmission. J Biol Dyn 4:296–314

    Article  PubMed  Google Scholar 

  • National Health and Family Planning Commission of China (NHFPC) (2015) Epidemic situation. http://www.nhfpc.gov.cn. Accessed 27 July 2015

  • Ruan S, Wei J (2003) On the zeros of transcendental functions with applications to stability of delay differential equations with two delays. Dyn Contin Discrete Impulse Syst Ser A Math Anal 10:863–874

    Google Scholar 

  • Ruan S, Xiao D, Beier JC (2008) On the delayed Ross–Macdonald model for malaria transmission. Bull Math Biol 70:1098–1114

    Article  PubMed Central  PubMed  Google Scholar 

  • Samanta GP (2010) Permanence and extinction for a nonautonomous avian-human influenza epidemic model with distributed time delay. Math. Comput. Model. 52:1794–1811

    Article  Google Scholar 

  • Tuncer N, Martcheva M (2013) Modeling seasonality in avian influenza H5N1. J Biol Syst 21:1–30

    Article  Google Scholar 

  • World Health Organisation (WHO) (2014) Human infection with avian influenza A (H7N9) virus (update). http://www.who.int/csr/don/2014_-02_-24/en/. Accessed 24 Feb 2014

  • World Health Organization (WHO) (2015) Influenza. http://www.who.int/topics/influenza/en/. Accessed 27 July 2015

  • World Organisation for Animal Health (OIE) (2013) OIE expert mission finds live bird markets play a key role in poultry and human infections with influenza A (H7N9). Paris. http://www.oie.int/en/for-the-media/press-releases/detail/article/oie-expert-mission-finds-live-bird-markets-play-a-key-role-in-poultry-and-human-infections-with-infl/. Accessed 30 April 2013

Download references

Acknowledgments

This work was partially supported by the National Natural Science Foundation (NNSF) of China (No. 11371161 and No. 11228104).

Author information

Authors and Affiliations

  1. School of Mathematics and Statistics, Central China Normal University, Wuhan, 430079, China

    Sanhong Liu & Xinan Zhang

  2. Department of Basic Education, Wenhua College, Wuhan, 430074, Hubei, China

    Sanhong Liu

  3. Department of Mathematics, University of Miami, Coral Gables, FL, 33124-4250, USA

    Shigui Ruan

Authors
  1. Sanhong Liu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Shigui Ruan
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Xinan Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Shigui Ruan.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Liu, S., Ruan, S. & Zhang, X. On avian influenza epidemic models with time delay. Theory Biosci. 134, 75–82 (2015). https://doi.org/10.1007/s12064-015-0212-8

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12064-015-0212-8

Keywords

Search

Navigation