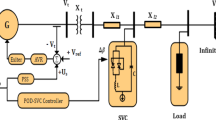
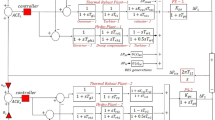
Abstract
Current power system stabilizer designs, including fuzzy-PID and Lead-Lag compensators, need help with adaptability and complexity in diverse and evolving power system environments. Conventional tuning methods like the Newton–Raphson approach and optimization strategies like particle swarm optimization, genetic algorithms, and cuckoo search algorithms face challenges in achieving optimal performance for Fractional Order Proportional Integral Derivative (FOPID) controllers. There is a critical need for innovative tuning methods that offer enhanced adaptability and performance in complex power system stability analysis. This research contributes to the advancement of power system stability analysis, specifically in SMIB systems, offering insights into optimizing FOPID controllers utilizing the innovative Harris Hawks Optimization (HHO) algorithm. The work expects these findings to broaden the implications for power system control and enhance the stability of Single Machine Infinite Bus (SMIB) systems, thus fostering the resilience and reliability of modern electrical infrastructure. The FOPID controller encompasses fractional order parameters, encompassing proportional, integral, and derivative gain, integral order, and derivative order, each exerting a substantial influence on control responses and stability. This research harnesses HHO, an optimization technique inspired by nature, to fine-tune FOPID parameters. The investigation involves initializing the SMIB model, formulating an objective function to minimize control errors, and employing HHO iteratively to refine the FOPID controller. The outcomes reveal enhanced stability, diminished overshoot, accelerated settling time, and transient response.









Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Data availability
No datasets were generated or analysed during the current study.
References
de Ayres Junior FACC, da Costa Junior CT, de Medeiros RLP, Barra Junior W, Das Neves CC, Lenzi MK, de Veroneze GM (2018) A fractional order power system stabilizer applied on a small-scale generation system. Energies 11(8):2052. https://doi.org/10.3390/en11082052
El-Dabah MA, Kamel S, Abido MAY, Khan B (2022) Optimal tuning of fractional-order proportional, integral, derivative and tilt-integral-derivative based power system stabilizers using Runge Kutta optimizer. Eng Rep 4(6):e12492. https://doi.org/10.1002/eng2.12492
Nocoń A, Paszek S (2023) A comprehensive review of power system stabilizers. Energies 16(4):1945. https://doi.org/10.3390/en16041945
Nogueira FG, Junior WB, da Costa Junior CT, Lana JJ (2022) LPV-based power system stabilizer: identification, control and field tests. Control Eng Pract 72:53–67. https://doi.org/10.1016/j.conengprac.2017.11.004
Abdulkhader K, Haseena JJ, Mathew AT (2022) Fractional-order lead-lag compensator-based multi-band power system stabilizer design using a hybrid dynamic GA-PSO algorithm. IET Gener Transm Distrib 12(13):3248–3260. https://doi.org/10.1049/iet-gtd.2017.1087
Rafique Z, Khalid HM, Muyeen SM, Kamwa I (2022) Bibliographic review on power system oscillations damping: an era of conventional grids and renewable energy integration. Int J Electr Power Energy Syst 136(107556):1–20. https://doi.org/10.1016/j.ijepes.2021.107556
Khalid HM, Peng JC-H (2016) Tracking electromechanical oscillations: an enhanced maximum-likelihood based approach. IEEE Trans Power Syst 31(3):1799–1808. https://doi.org/10.1109/TPWRS.2015.2441109
Khalid H, Flitti F, Mahmoud M, Hamdan M, Muyeen S, Dong Z (2023) WAMS operations in modern power grids: a median regression function-based state estimation approach towards cyber attacks. Sustain Energy Grid Netw 34:101009. https://doi.org/10.1016/j.segan.2023.101009
Devarapalli R, Bhattacharyya B (2020) A hybrid modified grey wolf optimization-sine cosine algorithm-based power system stabilizer parameter tuning in a multimachine power system. Opt Control Appl Methods 41(4):1143–1159. https://doi.org/10.1002/oca.2591
Ray PK, Paital SR, Mohanty A, Eddy FYS, Gooi HB (2022) A robust power system stabilizer for enhancement of stability in power system using adaptive fuzzy sliding mode control. Appl Soft Comput 73:471–481. https://doi.org/10.1016/j.asoc.2018.08.033
Du W, Dong W, Wang Y, Wang H (2020) A method to design power system stabilizers in a multi-machine power system based on a single-machine infinite-bus system model. IEEE Trans Power Syst 36(4):3475–3486. https://doi.org/10.1109/TPWRS.2020.3041037
Peres W, Coelho FCR, Costa JNN (2020) A pole placement approach for multi-band power system stabilizer tuning. Int Trans Electr Energy Syst 30(10):e12548. https://doi.org/10.1002/2050-7038.12548
Nangrani SP (2023) state of the art fractional order controller for power system stabilizer. J Intell Fuzzy Syst 36(3):2165–2173. https://doi.org/10.3233/JIFS-169928
Bingi K, Rosdiazli I, Mohd NK, Sabo MH, Vivekananda RH (2020) Fractional-order systems and PID controllers, vol 264. Springer, Cham
Nithilasaravanan K, Thakwani N, Mishra P, Kumar V, Rana KPS (2023) Efficient control of integrated power system using self-tuned fractional-order fuzzy PID controller. Neural Comput Appl 31:4137–4155. https://doi.org/10.1007/s00521-017-3309-9
Guha D, Roy PK, Banerjee S, Padmanaban S, Blaabjerg F, Chittathuru D (2020) Small-signal stability analysis of hybrid power system with quasi-oppositional sine cosine algorithm optimized fractional order PID controller. IEEE Access 8:155971–155986
Hassan MK, Amiri A, Marhaban H, Juraiza A (2022) Optimal tuning of fractional-order PID controller for electric power-assisted steering (EPAS) system using particle swarm optimization (PSO). In: Mariappan M, Arshad MR, Akmeliawati R, Chong CS (eds) Control Engineering in robotics and industrial automation: malaysian society for automatic control engineers (MACE) technical series. Springer, Cham, pp 169–182. https://doi.org/10.1007/978-3-030-74540-0_6
Jaiswal S, Kumar CS, Seepana MM, Babu GUB (2020) Design of fractional order PID controller using genetic algorithm optimization technique for the non-linear system. Chem Prod Process Model 15(2):20190072. https://doi.org/10.1515/cppm-2019-0072
Varshney T, Bhadoria VS, Sonwane P, Singh N (2022) Optimization of fractional-order pid controller (FOPID) using cuckoo search. In: Mathur G, Bundele M, Lalwani M, Paprzycki M (eds) Proceedings of 2nd international conference on artificial intelligence: advances and applications (ICAIAA). Springer, Singapore, pp 649–657. https://doi.org/10.1007/978-981-16-6332-1_53
Munagala VK, Jatoth RK (2021) Design of fractional-order PID/PID controller for DC motor speed control using Harris Hawks optimization. Intell Algorithms Anal Control Dyn Syst. https://doi.org/10.1007/978-981-15-8045-1_11
Heidari AA, Mirjalili S, Faris H, Aljarah I, Mafarja M, Chen H (2019) Harris hawks optimization: algorithm and applications. Futur Gener Comput Syst 97:849–872. https://doi.org/10.1016/j.future.2019.02.028
Mahdavian M, Amini AA, Hashemi M (2022) Design of a PID-PSS power system stabilizer for a single-machine infinite-bus power system. Signal Process Renew Energy 6(2):67–83
Ray PK, Paital SR, Mohanty A, Eddy FYS, Krishnan A, Gooi HB, and Amaratunga GAJ (2021) Firefly algorithm scaled fractional order fuzzy PID based PSS for transient stability improvement. In: 2021, the 19th international Carpathian control conference (ICCC), 428–433. https://doi.org/10.1109/CarpathianCC.2018.8399668
Ibrahim NM, El-said EA, Attia HE, Hemade BA (2024) Enhancing power system stability: an innovative approach using coordination of FOPID controller for PSS and SVC FACTS device with MFO algorithm. Electr Eng 106(3):2265–2283
Acknowledgements
The authors would like to express their gratitude to Department of Electrical and Electronics Engineering, Oriental University, Indore, Madhya Pradesh for all of their assistance and encouragement in carrying out this research and publishing this paper.
Funding
No Funding.
Author information
Authors and Affiliations
Contributions
Yogesh Kalidas Kirange: Conceptualization, Methodology, Software, Validation, Formal Analysis, Investigation, Resources, Data Curation, Writing-Original Draft Preparation, Writing-Review Editing and Visualization. Pragya Nema: Supervision, Writing—original draft, Writing—review & editing.
Corresponding author
Ethics declarations
Conflict of interest
The author declares that there is no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix: I
Appendix: I
Summary of abbreviations.
Symbol | Description | SI Unit |
|---|---|---|
Vref | reference voltage signal for the generator’s excitation system | Volt |
Vm | Nominal or rated voltage | Volt |
KP | Proportional gain | Unitless |
Δδ | Deviation in rotor angle from its equilibrium position | Radians |
KI | Integral gain | Unitless |
KD | Derivative gain | Unitless |
t | Time | Seconds |
Kp1 | Fractional order proportional gain | Unitless |
Ki1 | Fractional order integral gain | Unitless |
Kd1 | Fractional order derivative gain | Unitless |
α | Fractional order of the integral term | Unitless |
β | Fractional order of the derivative term | Unitless |
\({\text{P}}_{\text{e}}\) | Electrical power | Watt |
\(\text{E}\) E | The internal voltage of the generator | Volt |
\({\text{V}}_{\infty}\) | Voltage magnitude at the infinite bus | Volt |
δ | Rotor angle of the generator | Radian |
δ∞ | Phase angle at the infinite bus | Degree |
\({\text{X}}_{\text{d}}\) | Synchronous reactance | Ohm |
Xd’ | Transient reactance | Ohm |
Xd’’ | Sub transient reactance | Ohm |
\(\text{M}\) | Rotor’s inertia | Kg-M2 |
\(\frac{dt}{d\omega }\) | Rate of change of angular velocity or angular acceleration | Rad/Sec2 |
\({\text{P}}_{\text{m}}\) | Mechanical power input | Watt |
\({P}_{FOPID}\) | Power output from the FOPID controller | Watt |
\({P}_{mech}\) | Mechanical power input | Watt |
\(\text{D}\) | Damping coefficient | Unitless |
ꞷ | Actual angular velocity | Rad/Sec |
Ꞷs | Synchronous angular velocity | Rad/Sec |
\(\frac{d\delta }{dt}\) | Rate of change of the rotor angle | Rad/Sec2 |
\(\text{e}\left(\text{t}\right)\) | Error signal at time \(\text{t}\) t | – |
\(\Gamma\) | The gamma function computes a real-valued function’s integral over a given range | – |
\({x}_{i}\left(t+1\right)\) | New position of the \({i}^{th}\) hawk | – |
\({x}_{i}\left(t\right)\) | Current position of the \({i}^{th}\) hawk | – |
\({V}_{i}\left(t+1\right)\) | Velocity or step size of the \({i}^{th}\) hawk at time t + 1 | – |
\(r\) | Random number | – |
\({p}_{1}\), \({p}_{2}\) | Predefined probabilities | – |
J(Kp1, Ki1, Kd1, α, β | The objective function to be minimised | – |
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Kirange, Y.K., Nema, P. Optimising SMIB system stability: FOPID controller tuning via Harris hawks optimisation. Evol. Intel. 18, 16 (2025). https://doi.org/10.1007/s12065-024-00991-y
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s12065-024-00991-y