Abstract
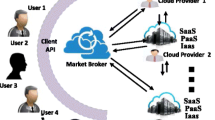
Taking advantage of the huge potential of consumers’ untapped computing power, self-organizing cloud is a novel computing paradigm where the consumers are able to contribute/sell their computing resources. Meanwhile, host machines held by the consumers are connected by a peer-to-peer (P2P) overlay network on the Internet. In this new architecture, due to large and varying multitudes of resources and prices, it is inefficient and tedious for consumers to select the proper resource manually. Thus, there is a high demand for a scalable and automatic mechanism to accomplish resource allocation. In view of this challenge, this paper proposes two novel economic strategies based on mechanism design. Concretely, we apply the Modified Vickrey Auction (MVA) mechanism to the case where the resource is sufficient; and the Continuous Double Auction (CDA) mechanism is employed when the resource is insufficient. We also prove that aforementioned mechanisms have dominant strategy incentive compatibility. Finally, extensive experiment results are conducted to verify the performance of the proposed strategies in terms of procurement cost and execution efficiency.






Similar content being viewed by others
References
Mell P, Grance T (2011) The nist definition of cloud computing (draft), NIST special publication, [Online]. Available: http://www.nist.gov/itl/cloud/upload/cloud-defv15.pdf
Armbrust M, Fox A, Griffith R, Joseph AD , Katz R, Konwinski A, Lee G, Patterson D, Rabkin A, Stoica I, et al. (2010) “A view of cloud computing,”. Commun ACM 53(4):50–58
Amazon Web Service. [Online]. Available: http://aws.amazon.com/
Microsoft Windows Azure. [Online]. Available: http://www.microsoft.com/
Google AppEngine. [Online]. Available: http://code.google.com/appengine/
Wang H, Wang F, Liu J, Groen J (2012) Measurement and utilization of customer-provided resources for cloud computing. In: Proceedings IEEE INFOCOM 2012
Di S, Wang CL (2013) Dynamic optimization of multiattribute resource allocation in self-organizing clouds. Parallel Distrib Syst IEEE Trans 24(3):464–478
SpotCloud. [Online]. Available: http://www.spotcloud.com
Di S, Wang CL, Zhang W, Cheng L (2011) Probabilistic best-fit multi-dimensional range query in self-organizing cloud. In: 2011 International conference on parallel processing (ICPP)
Wang H, Wang F, Liu J, Xu K, Wu D, Lin Q (2013) Resource provisioning on customer-provided clouds: Optimization of service availability. In: IEEE International conference on communications (ICC) 2013
Di S, Wang C, Cheng L, Chen L (2011) Social-optimized win-win resource allocation for self-organizing cloud. In: International conference on cloud and service Computing (CSC) 2011
Mihailescu M , Teo YM (2010) Dynamic resource pricing on federated clouds. In: 10th IEEE/ACM international conference on cluster, cloud and grid computing (CCGrid) 2010
Bichler M, Kalagnanam J, Katircioglu K, King AJ , Lawrence RD , Lee HS, Lin GY, Lu Y (2002) Applications of flexible pricing in business-to-business electronic commerce. IBM Syst J 41(2):287–302
McAfee RP, McMillan J (1987) Auctions and bidding. J Econ Lit 25(2):699–738
Narahari Y, Garg D, Narayanam R, Prakash H (2009) Game theoretic problems in network economics and mechanism design solutions. Springer, New York
Jackson MO (2000) The encyclopedia of life support systems
Prasad A , Rao S (2014) A mechanism design approach to resource procurement in cloud computing. Comput IEEE Trans 63(1 ):17–30
Kong Z, Xu CZ , Guo M (2011) Mechanism design for stochastic virtual resource allocation in non-cooperative cloud systems In: IEEE International Conference on Cloud Computing (CLOUD) 2011, pp 614–621
Mihailescu M , Teo YM (2010) Strategy-proof dynamic resource pricing of multiple resource types on federated clouds. In: Algorithms and architectures for parallel processing. Springer, pp 337–350
Gibbard A (1973) Manipulation of voting schemes: a general result. Econometrica: J Econ Soc:587–601
Satterthwaite MA (1975) Strategy-proofness and arrow’s conditions: Existence and correspondence theorems for voting procedures and social welfare functions. J Economic Theory 10(2):187–217
Myerson RB (1981) Optimal auction design. Math Oper Res 6(1):58–73
Friedman D (1993) The double auction market institution: A survey. Double Auction Market: Inst Theor Evid 14:3–25
Klemperer P (1999) Auction theory: A guide to the literature. J Econ Surv 13(3):227–286
Gode DK, Sunder S (1993) Allocative efficiency of markets with zero-intelligence traders: Market as a partial substitute for individual rationality. J Polit Econ 101(1):119–137
Leininger W, Linhart PB, Radner R (1989) Equilibria of the sealed-bid mechanism for bargaining with incomplete information. J Econ Theor 48(1 ):63–106
Mas-Colell A, Whinston M, Green J (1995) Microeconomics
Generatedata. [Online]. Available: http://www.generatedata.com/
Rimal BP, Choi E, Lumb I (2009) A taxonomy and survey of cloud computing systems. In: 5th International Joint Conference on INC, IMS and IDC, 2009. NCM’09
Buyya R, Yeo CS, Venugopal S, Broberg J, Brandic I (2009) Cloud computing and emerging it platforms: Vision, hype, and reality for delivering computing as the 5th utility. Futur Gener Comput Syst 25(6):599–616
Rochwerger B, Breitgand D, Levy E, Galis A, Nagin K, Llorente IM, Montero R, Wolfsthal Y, Elmroth E, Cáceres J, et al. (2009) The reservoir model and architecture for open federated cloud computing. IBM J Res Dev 53(4):1–11
Bermbach D, Klems M, Tai S, Menzel M (2011) Metastorage: A federated cloud storage system to manage consistency-latency tradeoffs. In: IEEE International conference on cloud computing (CLOUD) 2011
Rochwerger B, Breitgand D, Epstein A, Hadas D , Loy I, Nagin K, Tordsson J, Ragusa C, Villari M, Clayman S, et al. (2011) Reservoirwhen one cloud is not enough. IEEE Comput 44(3):44–51
Avetisyan A , Campbell R, Gupta I, Heath M, et al. (2010) Open cirrus: A global cloud computing testbed. Comput 43(4):35–43
Samaan N (2014) A novel economic sharing model in a federation of selfish cloud providers. Parallel Distrib Syst IEEE Trans 25(1):12–21
Toosi AN , Calheiros RN, Thulasiram RK, Buyya R (2011) Resource provisioning policies to increase iaas provider’s profit in a federated cloud environment. In: 13th International conference on high performance computing and communications (HPCC), 2011 IEEE
Gomes ER, Vo QB, Kowalczyk R (2012) Pure exchange markets for resource sharing in federated clouds. Concurr Comput Prac Experience 24(9):977–991
Song B, Hassan MM, Huh EN (2009) A novel cloud market infrastructure for trading service. In: International conference on computational science and its applications, ICCSA’09
Buyya R , Abramson D, Giddy J, Stockinger H (2002) Economic models for resource management and scheduling in grid computing. Concurr Comput Pract Experience 14(13-15):1507–1542
Xhafa F, Kolodziej J (2010) Game-theoretic, market and meta-heuristics approaches for modelling scheduling and resource allocation in grid systems. In: 2010 International conference on P2P, parallel, grid, cloud and internet computing(3PGCIC)
Zaman S, Grosu D (2013) A combinatorial auction-based mechanism for dynamic vm provisioning and allocation in clouds. Cloud Comput IEEE Trans 1(2 ):129–141
Chard K, Bubendorfer K (2013) High performance resource allocation strategies for computational economies. Parallel Distrib Syst IEEE Trans 24(1):72–84
Ge Y, Zhang Y, Qiu Q, Y.-H. Lu (2012) A game theoretic resource allocation for overall energy minimization in, mobile cloud computing system. In: Proceedings of the 2012 ACM/IEEE International symposium on low power electronics and design
Acknowledgments
This paper is partly supported by project National Science Foundation of China under Grant 91318301.
Author information
Authors and Affiliations
Corresponding author
Appendix A: Proof of Theorem 1
Appendix A: Proof of Theorem 1
We introduce [15] and prove as follows.
Proof
First of all, we consider bidder 1. His value is v 1j and bid is b 1j . The other bidders have bids b 2j , ... , b n j and valuations v 2j , ... , v n j . Due to the reverse auction, the utility value of bidder 1 is b 1j − v 1j . We consider the following cases.
Case 1: v 1j ≤ m i n(b 2j , ... , b n j ). There are two sub-cases here: b 1j ≤ m i n(b 2j , ... b n j ) and b 1j > m i n(b 2j , ... b n j )).
Case 2: v 1j >m i n(b 2j , ... , b n j ). There are two sub-cases here: b 1j ≤ m i n(b 2j , ... b n j ) and b 1j > m i n(b 2j , ... b n j )).
We analyze these cases separately below.
Case 1: v 1j ≤ m i n(b 2j , ... , b n j ).
-
Let b 1j ≤ m i n(b 2j , ... b n j ). This implies that bidder 1 is the winner, which refers that u 1j = m i n(b 2j , ... b n j )−v 1j ≥ 0.
-
Let b 1j >m i n(b 2j , ... b n j ). This means that bidder 1 is not the winner, which in turn means that u 1j = 0.
-
Let b 1j = v 1j , then since v 1j ≤ m i n(b 2j , ... , b n j ), we have u 1j = m i n(b 2j , ... b n j )−v 1j .
Thus, if b 1j = v 1j , the utility u 1j is greater than or equal to the maximum utility obtainable. Thus, whatever the values of b 2j , ... b n j , it is a best response for player 1 to bid v 1j . Thus, b 1j = v 1j is a weakly dominant strategy for bidder 1.
Case 2: v 1j >m i n(b 2j , ... , b n j ).
-
Let b 1j ≤ m i n(b 2j , ... b n j ). This implies that bidder 1 is the winner, and the payoff is given by u 1j = m i n(b 2j , ... b n j )−v 1j < 0.
-
Let b 1j >m i n(b 2j , ... b n j ). This means that bidder 1 is not the winner. Therefore u 1j = 0.
-
Let b 1j = v 1j , then bidder 1 is not the winner and thus u 1j = 0.
From the above analysis, it is clear that b 1j = v 1j is a best response strategy for player 1 in Case 2 also. Combining our analysis of Case 1 and Case 2, we have that
where \( \widehat {b_{1j}} \in {\Theta }_{1j}, \forall b_{2j}\in {\Theta }_{2j},...,b_{nj}\in {\Theta }_{nj} \).
Also, we can show that, for any \( b_{1j}^{\prime } \neq v_{1j} \), we can always find that for ∀b 2j ∈ Θ2j , ... , b n j ∈ Θ n j , such that
Thus b 1j = v 1j is a weakly dominant strategy for bidder 1. Using almost similar arguments, we can show that b i j = v i j is a weakly dominant strategy for bidder i where i = 2, ... , n. Therefor v 1j , ... , v n j is a weakly dominant strategy equilibrium. □
Rights and permissions
About this article
Cite this article
Wu, X., Liu, M., Dou, W. et al. A scalable and automatic mechanism for resource allocation in self-organizing cloud. Peer-to-Peer Netw. Appl. 9, 28–41 (2016). https://doi.org/10.1007/s12083-014-0309-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12083-014-0309-8