Skip to main content

Advertisement

Springer Nature Link
Log in

A privacy-preserving and efficient byzantine consensus through multi-signature with ring

  • Published:
Peer-to-Peer Networking and Applications Aims and scope Submit manuscript

Abstract

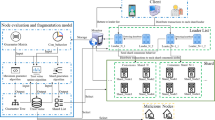
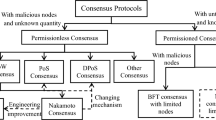
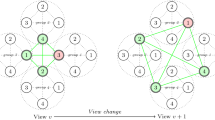
The consortium blockchain has three challenges in terms of performance, security, and privacy when adopting the Practical Byzantine Fault Tolerance (PBFT) protocol. The throughput and scalability of consortium blockchain are focused on meanwhile the privacy protection can hardly be ignored. This work proposes a privacy-preserving multi-signature and hierarchical Byzantine consensus protocol. Specifically, the signature combines a ring signature and a Schnorr one to provide three levels of privacy protection. The consensus protocol layers the network nodes into different clusters, which overcomes the shortcomings of PBFT and Schnorr signature. The theoretical analysis proves the security and privacy of the protocol and expounds the application scenarios, and the efficiency evaluation shows that the signature verification speed is 6.28 times faster than the Schnorr scheme, and the consensus in a 250-nodes network is 51.3% faster than the Schnorr-based PBFT consensus.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7

Similar content being viewed by others

References

  1. Nakamoto S (2008) Bitcoin: A peer-to-peer electronic cash system. https://bitcoin.org/bitcoin.pdf

  2. Wood G et al (2014) Ethereum: A secure decentralised generalised transaction ledger. Ethereum Project Yellow Paper 151:1–32

    Google Scholar 

  3. Clark J, Edward A, Felten W (2015) Research perspectives and challenges for bitcoin and cryptocurrencies. https://eprint.iacr.org/2015/261.pdf

  4. Conti M, Kumar ES, Lal C, Ruj S (2018) A survey on security and privacy issues of bitcoin. IEEE Communications Surveys & Tutorials 20(4):3416–3452

    Article  Google Scholar 

  5. Zamani M, Movahedi M, Raykova M (2018) Rapidchain: Scaling blockchain via full sharding. Proceedings of the 2018 ACM SIGSAC Conference on Computer and Communications Security pp 931–948

  6. Kokoris-Kogias E, Jovanovic P, Gasser L, Gailly N, Syta E, Ford B (2018) Omniledger: A secure, scale-out, decentralized ledger via sharding. 2018 IEEE Symposium on Security and Privacy (SP) pp 583–598

  7. Gilad Y, Hemo R, Micali S, Vlachos G, Zeldovich N (2017) Algorand: Scaling byzantine agreements for cryptocurrencies. Proceedings of the 26th Symposium on Operating Systems Principles pp 51–68

  8. Feng X, Ma J, Miao Y, Meng Q, Liu X, Jiang Q, Li H (2019) Pruneable sharding-based blockchain protocol. Peer-to-Peer Netwo Appl 12(4):934–950

    Article  Google Scholar 

  9. Castro M, Liskov B et al (1999) Practical byzantine fault tolerance. OSDI 99:173–186

    Google Scholar 

  10. Kogias EK, Jovanovic P, Gailly N, Khoffi I, Gasser L, Ford B (2016) Enhancing bitcoin security and performance with strong consistency via collective signing. 25th \(\{\)usenix\(\}\) security symposium (\(\{\)usenix\(\}\) security 16) pp 279–296

  11. Androulaki E, Barger A, Bortnikov V, Cachin C, Christidis K, De Caro A, Enyeart D, Ferris C, Laventman G, Manevich Y, et al. (2018) Hyperledger fabric: a distributed operating system for permissioned blockchains. Proceedings of the thirteenth EuroSys conference pp 1–15

  12. Bessani A, Sousa J, Alchieri EE (2014) State machine replication for the masses with bft-smart. 2014 44th Annual IEEE/IFIP International Conference on Dependable Systems and Networks pp 355–362

  13. Sousa J, Bessani A (2012) From byzantine consensus to bft state machine replication: A latency-optimal transformation. 2012 Ninth European Dependable Computing Conference pp 37–48

  14. Ristenpart T, Yilek S (2007) The power of proofs-of-possession: Securing multiparty signatures against rogue-key attacks. Annual International Conference on the Theory and Applications of Cryptographic Techniques pp 228–245

  15. Li CM, Hwang T, Lee NY (1994) Threshold-multisignature schemes where suspected forgery implies traceability of adversarial shareholders. Workshop on the Theory and Application of of Cryptographic Techniques pp 194–204

  16. Harn L (1994) Group-oriented (t, n) threshold digital signature scheme and digital multisignature. IEE Proceedings-Computers and Digital Techniques 141(5):307–313

    Article  Google Scholar 

  17. Horster P, Michels M, Petersen H (1995) Meta-multisignature schemes based on the discrete logarithm problem. Information Security the Next Decade pp 128–142

  18. Rivest RL, Shamir A, Tauman Y (2001) How to leak a secret. International Conference on the Theory and Application of Cryptology and Information Security pp 552–565

  19. Blum M, Feldman P, Micali S (1988) Non-interactive zero-knowledge and its applications. Proceedings of the twentieth annual ACM symposium on Theory of computing pp 103–112

  20. Wu H, Wang F (2014) A survey of noninteractive zero knowledge proof system and its applications. Sci World J

  21. Schnorr CP (1991) Efficient signature generation by smart cards. J Cryptol 4(3):161–174

    Article  MathSciNet  Google Scholar 

  22. Maxwell G, Poelstra A, Seurin Y, Wuille P (2018) Simple schnorr multi-signatures with applications to bitcoin. Des Codes Crypt 87(9):2139–2164

    Article  MathSciNet  Google Scholar 

  23. Kwon J (2014) Tendermint: Consensus without mining. https://tendermint.com/static/docs/tendermint.pdf

  24. Li P, Wang G, Chen X, Long F, Xu W (2020) Gosig: a scalable and high-performance byzantine consensus for consortium blockchains. Proceedings of the 11th ACM Symposium on Cloud Computing pp 223–237

  25. Johnson D, Menezes A, Vanstone S (2001) The elliptic curve digital signature algorithm (ecdsa). Int J Inf Secur 1(1):36–63

    Article  Google Scholar 

  26. Li Y, Qiao L, Lv Z (2021) An optimized byzantine fault tolerance algorithm for consortium blockchain. Peer-to-Peer Networking and Applications pp 1–14

  27. Bresson E, Stern J, Szydlo M (2002) Threshold ring signatures and applications to ad-hoc groups. Annual International Cryptology Conference pp 465–480

  28. Chow SS, Hui LC, Yiu SM (2004) Identity based threshold ring signature. International Conference on Information Security and Cryptology pp 218–232

  29. Herranz J, Sáez G (2004) Distributed ring signatures for identity-based scenarios. IACR Cryptol ePrint Arch

  30. Boneh D, Gentry C, Lynn B, Shacham H (2003) Aggregate and verifiably encrypted signatures from bilinear maps. International Conference on the Theory and Applications of Cryptographic Techniques pp 416–432

  31. Boneh D, Lynn B, Shacham H (2001) Short signatures from the weil pairing. International conference on the theory and application of cryptology and information security pp 514–532

  32. Drijvers M, Edalatnejad K, Ford B, Kiltz E, Loss J, Neven G, Stepanovs I (2019) On the security of two-round multi-signatures. 2019 IEEE Symposium on Security and Privacy (SP) pp 1084–1101

  33. Damgård I, Orlandi C, Takahashi A, Tibouchi M (2021) Two-round n-out-of-n and multi-signatures and trapdoor commitment from lattices. IACR International Conference on Public-Key Cryptography pp 99–130

  34. Goodell B, Noether S (2018) Thring signatures and their applications to spender-ambiguous digital currencies. IACR Cryptol ePrint Arch

  35. Leiba O, Yitzchak Y, Bitton R, Nadler A, Shabtai A (2018) Incentivized delivery network of iot software updates based on trustless proof-of-distribution. 2018 IEEE European Symposium on Security and Privacy Workshops (EuroS&PW) pp 29–39

  36. Badr MM, Al Amiri W, Fouda MM, Mahmoud MM, Aljohani AJ, Alasmary W (2020) Smart parking system with privacy preservation and reputation management using blockchain. IEEE Access 8:150823–150843

    Article  Google Scholar 

  37. Nick J, Ruffing T, Seurin Y, Wuille P (2020) Musig-dn: Schnorr multi-signatures with verifiably deterministic nonces. Proceedings of the 2020 ACM SIGSAC Conference on Computer and Communications Security pp 1717–1731

  38. Nick J, Ruffing T, Seurin Y (2021) Musig2: Simple two-round schnorr multi-signatures. Annual International Cryptology Conference pp 189–221

Download references

Acknowledgements

This work was supported in part by Open project of Sichuan Provincial Key Laboratory of Intelligent Terminal Co built by Province and City (SCITLAB-1014), and in part by Sichuan Science and Technology Program (2021YFG0305).

Author information

Authors and Affiliations

  1. School of Information and Software Engineering, University of Electronic Science and Technology of China, Chengdu, China

    Xiaohua Wu, Hongji Ling, Huan Liu & Fangjian Yu

Authors
  1. Xiaohua Wu
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Hongji Ling
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Huan Liu
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. Fangjian Yu
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding authors

Correspondence to Xiaohua Wu or Hongji Ling.

Ethics declarations

Competing interests

The authors have no competing interests to declare that are relevant to the content of this article.

Additional information

Publisher’s Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Wu, X., Ling, H., Liu, H. et al. A privacy-preserving and efficient byzantine consensus through multi-signature with ring. Peer-to-Peer Netw. Appl. 15, 1669–1684 (2022). https://doi.org/10.1007/s12083-022-01317-4

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12083-022-01317-4

Keywords