Skip to main content
Springer Nature Link
Log in

Minimum sizes of identifying codes in graphs differing by one vertex

  • Published:
Cryptography and Communications Aims and scope Submit manuscript

    We’re sorry, something doesn't seem to be working properly.

    Please try refreshing the page. If that doesn't work, please contact support so we can address the problem.

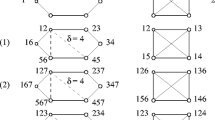
Abstract

Let G be a simple, undirected graph with vertex set V. For v ∈ V and r ≥ 1, we denote by B G,r (v) the ball of radius r and centre v. A set \({\cal C} \subseteq V\) is said to be an r-identifying code in G if the sets \(B_{G,r}(v)\cap {\cal C}\), v ∈ V, are all nonempty and distinct. A graph G admitting an r-identifying code is called r-twin-free, and in this case the size of a smallest r-identifying code in G is denoted by γ r (G). We study the following structural problem: let G be an r-twin-free graph, and G * be a graph obtained from G by adding or deleting a vertex. If G * is still r-twin-free, we compare the behaviours of γ r (G) and \(\gamma_r(G^*)\), establishing results on their possible differences and ratios.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7

Similar content being viewed by others

References

  1. Berge, C.: Graphes, Gauthier-Villars: Paris, 1983. English translation: Graphs, North-Holland Publishing Co., Amsterdam (1985)

    MATH  Google Scholar 

  2. Bertrand, N., Charon, I., Hudry, O., Lobstein, A.: Identifying and locating-dominating codes on chains and cycles. Eur. J. Comb. 25, 969–987 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  3. Charon, I., Honkala, I., Hudry, O., Lobstein, A.: Structural properties of twin-free graphs. Electron. J. Comb. 14(1), R16 (2007)

    MathSciNet  Google Scholar 

  4. Charon, I., Honkala, I., Hudry, O., Lobstein, A.: Minimum sizes of identifying codes in graphs differing by one edge (submitted)

  5. Charon, I., Hudry, O., Lobstein, A.: On the structure of identifiable graphs. Electron. Notes Discrete Math. 22, 491–495 (2005)

    Article  Google Scholar 

  6. Charon, I., Hudry, O., Lobstein, A.: Extremal cardinalities for identifying and locating-dominating codes in graphs. Discrete Math. 307, 356–366 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  7. Chen, C., Lu, C., Miao, Z.: Identifying codes and locating-dominating sets on paths and cycles. Discrete Appl. Math. 159, 1540–1547 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  8. Diestel, R.: Graph Theory. Springer, Berlin (2005)

    MATH  Google Scholar 

  9. Foucaud, F., Guerrini, E, Kovše, M., Naserasr, R., Parreau, A., Valicov, P.: Extremal graphs for the identifying code problem. Eur. J. Combin. 32, 628–638 (2011)

    Article  MATH  Google Scholar 

  10. Frick, M., Fricke, G.H., Mynhardt, C.M., Skaggs, R.D.: Critical graphs with respect to vertex identification. Util. Mathematica 76, 213–227 (2008)

    MathSciNet  MATH  Google Scholar 

  11. Gravier, S., Moncel, J.: On graphs having a V ∖ { x } set as an identifying code. Discrete Math. 307, 432–434 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  12. Honkala, I.: An optimal edge-robust identifying code in the triangular lattice. Ann. Comb. 8, 303–323 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  13. Honkala, I.: On 2-edge-robust r-identifying codes in the king grid. Australasian Journal of Combinatorics 36, 151–165 (2006)

    MathSciNet  MATH  Google Scholar 

  14. Honkala, I., Laihonen, T.: On identifying codes that are robust against edge changes. Inf. Comput. 205, 1078–1095 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  15. Karpovsky, M.G., Chakrabarty, K., Levitin, L.B.: On a new class of codes for identifying vertices in graphs. IEEE Trans. Inf. Theory IT-44, 599–611 (1998)

    Article  MathSciNet  Google Scholar 

  16. Laihonen, T.: Optimal t-edge-robust r-identifying codes in the king lattice. Graphs Comb. 22, 487–496 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  17. Laihonen, T.: On edge-robust (1, ≤ ℓ)-identifying codes in binary Hamming spaces. Int. J. Pure Appl. Math. 36, 87–102 (2007)

    MathSciNet  MATH  Google Scholar 

  18. Lobstein, A.: A bibliography on watching systems, identifying, locating-dominating and discriminating codes in graphs. http://perso.telecom-paristech.fr/~lobstein/debutBIBidetlocdom.pdf. Accessed 23 August 2012

  19. Roberts, D.L., Roberts, F.S.: Locating sensors in paths and cycles: the case of 2-identifying codes. Eur. J. Combin. 29, 72–82 (2008)

    Article  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Télécom ParisTech & CNRS - LTCI UMR 5141, Institut Télécom, 46, rue Barrault, 75634, Paris Cedex 13, France

    Irène Charon, Olivier Hudry & Antoine Lobstein

  2. Department of Mathematics and Statistics, University of Turku, 20014, Turku, Finland

    Iiro Honkala

Authors
  1. Irène Charon
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Iiro Honkala
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Olivier Hudry
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. Antoine Lobstein
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Iiro Honkala.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Charon, I., Honkala, I., Hudry, O. et al. Minimum sizes of identifying codes in graphs differing by one vertex. Cryptogr. Commun. 5, 119–136 (2013). https://doi.org/10.1007/s12095-012-0078-2

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12095-012-0078-2

Keywords